山东省济宁市金乡县2022-2023学年下学期九年级第一次模拟学情检测数学试题

试卷更新日期：2023-03-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 实验测得，某种新型冠状病毒的直径是0.000000012米，0.000000012米用科学记数法可表示为（）

A、 $12 \times 1 0^{- 6}$ 米 B、 $1.2 \times 1 0^{- 7}$ 米 C、 $1.2 \times 1 0^{- 8}$ 米 D、 $120 \times 1 0^{- 9}$ 米

查看试题解析
2. 实数 $a$ ， $b$ ， $c$ 在数轴上的对应点的位置如图所示，则正确的结论是（）

A、 $| a | > 4$ B、 $c - b > 0$ C、 $a c > 0$ D、 $a + c > 0$

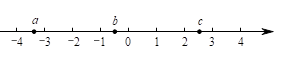查看试题解析
3. 如图，已知 $∠ 1 = ∠ 2$ ，那么添加下列一个条件后，仍无法判定 $△ A B C ∽ △ A D E$ 的是（）

A、 $∠ C = ∠ E$ B、 $∠ B = ∠ A D E$ C、 $\frac{A B}{A D} = \frac{B C}{D E}$ D、 $\frac{A B}{A D} = \frac{A C}{A E}$

查看试题解析
4. 若关于x的一元二次方程 $k x^{2} - 2 x - 1 = 0$ 有两个不相等的实数根，则k的取值范围是（）

A、 $k > - 1$ B、 $k > - 1 且 k \neq 0$ C、 $k < 1$ D、 $k < - 1 且 k \neq 0$

查看试题解析
5. 如图，已知AB为⊙O的弦，C为 $\overset{⌢}{A B}$ 的中点，点D在优弧 $\overset{⌢}{A B C}$ 上一点，连接AD下列式子一定正确的是（　　）

A、∠ADC＝∠B B、∠ADC+2∠B＝90° C、2∠ADC+∠B＝90° D、∠B＝30°

查看试题解析
6. 《四元玉鉴》是一部成就辉煌的数学名著，是宋元数学集大成者，也是我国古代水平最高的一部数学著作．该著作记载了“买椽多少”问题：“六贯二百一十钱，倩人去买几株椽．每株脚钱三文足，无钱准与一株椽”．大意是：现请人代买一批椽，这批椽的总售价为 $6210$ 文．如果每株椽的运费是3文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问 $6210$ 文能买多少株椽？设 $6210$ 元购买椽的数量为x株，则正确的方程是（）．

A、 $\frac{6210}{x - 1} = 3 x$ B、 $3 (x - 1) = 6210$ C、 $3 (x - 1) = \frac{6210}{x}$ D、 $3 (x - 1) = \frac{6210}{x - 1}$

查看试题解析
7. 关于x的不等式组 ${\begin{array}{l} 6 - 3 x < 0 \\ 2 x \leq a \end{array}$ 恰好有3个整数解，则a满足（）

A、 $a = 10$ B、 $10 \leq a < 12$ C、 $10 < a \leq 12$ D、 $10 \leq a \leq 12$

查看试题解析
8. 如图，等边 $△ A B C$ 的边长为6，P沿 $C \to B \to A$ 运动，Q沿 $B \to A \to C$ 运动，且速度都为每秒2个单位， $△ B P Q$ 面积为y，则y与运动时间x秒的函数的图象大致为（）

A、 B、 C、 D、

查看试题解析
9. 如图，在平面直角坐标系中，矩形 $O A B C$ 与反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象交于 $D$ ， $E$ 两点，矩形的顶点 $A$ ， $C$ 在坐标轴上， $O D ： D E = 10 ： 21$ ， $∠ O D E = 90 °$ ，若点 $D$ 的坐标为 $(2 ， 5)$ ，则下列结论错误的是（）

A、 $S_{△ O E C} = 10$ B、 $S_{△ D B E} = \frac{441}{20}$ C、 $\frac{B E}{E C} = \frac{21}{4}$ D、点 $E$ 的坐标为 $(\frac{25}{2} ， \frac{4}{5})$

查看试题解析
10. 如图，已知点 $A (4 ， 0) ， B (0 ， 3)$ ，直线l经过A、B两点，点 $C (x ， y)$ 为直线l在第一象限的动点，作 $△ A O C$ 的外接圆 $⊙ M$ ，延长 $C M$ 交 $⊙ M$ 于点Q，则 $△ O C Q$ 的面积最小值为（　　）

A、4 B、4.5 C、 $\frac{24}{5}$ D、 $\frac{96}{25}$

查看试题解析

二、填空题

11. 分解因式： $x y^{2} - x =$ ．

查看试题解析
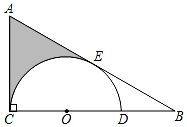
12. 已知点 $A (1 ， y_{1})$ ， $B (3 ， y_{2})$ 在反比例函数 $y = \frac{m - 2}{x}$ 的图象上，且 $y_{1} < y_{2}$ ，则m的取值范围是．

查看试题解析
13. 已知 $x_{1} 、 x_{2}$ 是方程 $x^{2} - k x + \frac{1}{4} k (k + 4) = 0$ 的两个根，且满足 $(x_{1} - 1) (x_{2} - 1) = \frac{13}{4}$ ，则k= ．

查看试题解析
14. 如图，以CD为直径的半圆与AB，AC相切于E，C两点，C，D，B三点共线，若弧DE的长为 $\frac{1}{3} π$ ， CD＝2，则阴影部分的面积为．

查看试题解析
15. 如图，抛物线 $y = - x^{2} + b x + c$ 与x轴交于点 $A (1 ， 0)$ 、点B，与y轴相交于点 $C (0 ， 3)$ ，下列结论：① $b = - 2$ ﹔②B点坐标为 $(- 3 ， 0)$ ， ③抛物线的顶点坐标为 $(- 1 ， 3)$ ， ④直线 $y = h$ 与抛物线交于点D、E，若 $D E < 2$ ，则h的取值范围是 $3 < h < 4$ ﹔⑤在抛物线的对称轴上存在一点Q，使 $△ Q A C$ 的周长最小，则Q点坐标为 $(- 1 ， 2)$ ．其中正确的有．

查看试题解析

三、解答题

16.

(1)、计算： ${(- 1)}^{2023} + | \sqrt{3} - 2 | + t a n 60 ° + {(π - 3.14)}^{0} + {(\frac{1}{2})}^{- 2}$

(2)、先化简，再求值： $\frac{x - 3}{x^{2} - 1} \div \frac{x - 3}{x^{2} + 2 x + 1} - (\frac{1}{x - 1} + 1)$ ，其中x从-1，0，1，2，3中选取一个合适的数．

查看试题解析
17. 如图，在正方形网格中，△ABC的三个顶点都在格点上，结合所给的平面直角坐标系解答下列问题：
（ 1 ）将△ABC向右平移5个单位长度，画出平移后的△A₁B₁C₁；
（ 2 ）画出△ABC关于x轴对称的△A₂B₂C₂；
（ 3 ）将△ABC绕原点O 旋转180°，画出旋转后的△A₃B₃C₃；

查看试题解析
18. 我市为加快推进生活垃圾分类工作，对分类垃圾桶实行统一的外型、型号、颜色等，其中，可回收物用蓝色收集桶，有害垃圾用红色收集桶，厨余垃圾用绿色收集桶，其他垃圾用灰色收集桶．为了解学生对垃圾分类知识的掌握情况，某校宣传小组就“用过的餐巾纸应投放到哪种颜色的收集桶”在全校随机采访了部分学生，根据调查结果，绘制了如图所示的两幅不完整的统计图．
用过的餐巾纸投放情况统计图
根据图中信息，解答下列问题：

(1)、此次调查一共随机采访了名学生，在扇形统计图中，“灰”所在扇形的圆心角的度数为度；

(2)、补全条形统计图（要求在条形图上方注明人数）；

(3)、若该校有3600名学生，估计该校学生将用过的餐巾纸投放到红色收集桶的人数；

(4)、李老师计划从A，B，C，D四位学生中随机抽取两人参加学校的垃圾分类知识抢答赛，请用树状图法或列表法求出恰好抽中A，B两人的概率．

查看试题解析
19. 为提高数学学习的兴趣，某学校数学社团利用周日举行了测量旗杆高度的活动．已知旗杆的底座高1米，长8米，宽6米，旗杆位于底座中心．
测量方法如下：在地面上找一点D，用测角仪测出看旗杆AB顶B的仰角为67.4°，沿DE方向走4.8米到达C地，再次测得看旗杆顶B的仰角为73.5°．

(1)、求旗杆的高度．

(2)、已知夏至日时该地的最大太阳高度约为78°，试问夏至日旗杆顶B的影子能不能落在台阶上？（太阳高度角是指某地太阳光线与地平线的夹角．结果精确到0.1m，参考数据：tan67.4°≈2.4，tan73.5°≈ $\frac{24}{7}$ ， tan22.6°≈ $\frac{5}{12}$ ， tan16.5°≈ $\frac{7}{24}$ ， tan12°≈0.21）

查看试题解析
20. 云浮市各级公安交警部门提醒市民，骑车出行必须严格遵守“一盔一带”的规定，郁南县某商场同时购进 $A ， B$ 两种类型的头盔，已知购进3个A类头盔和4个B类头盔共需288元；购进6个A类头盔和2个B类头盔共需306元．

(1)、 $A ， B$ 两类头盔每个的进价各是多少元？

(2)、在销售中，该商场发现A类头盔每个售价50元时，每个月可售出100个；每个售价提高5元时，每个月少售出10个．设A类头盔每个x元（ $50 \leq x \leq 100$ ），y表示该商家每月销售A类头盔的利润（单位：元），求y关于x的函数解析式并求最大利润．

查看试题解析
21. 如图， $A B$ 为 $⊙ O$ 的直径，C为 $⊙ O$ 上一点，D为 $B A$ 延长线上一点， $∠ A C D = ∠ B$ ．

(1)、求证： $D C$ 为 $⊙ O$ 的切线；

(2)、若 $⊙ O$ 的半径为5， $s i n B = \frac{3}{5}$ ，求 $A D$ 的长．

查看试题解析
22. 如图1，直线 $y = - x + 5$ 与x轴、y轴分别交于B、C两点，经过B、C两点的抛物线与x轴的另一交点坐标为 $A （ - 1 ， 0 ）$ .

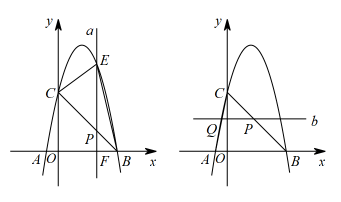(1)、求B、C两点的坐标及该抛物线所对应的函数关系式；

(2)、P在线段 $B C$ 上的一个动点（与B、C不重合），过点P作直线 $a ∥ y$ 轴，交抛物线于点E，交x轴于点F，设点P的横坐标为m.
①若点P的横坐标为m，请用m表示线段 $P E$ 的长度并写出m的取值范围；
②有人认为：当直线a与抛物线的对称轴重合时，线段 $P E$ 的值最大，你同意他的观点吗？请说明理由；
③过点P作直线 $b ∥ x$ 轴（图2），交 $A C$ 于点Q，那么在x轴上是否存在点R，使得 $△ P Q R$ 与 $△ B O C$ 相似？若存在，请求出点R的坐标；若不存在，请说明理由.

查看试题解析