山东省济南市历下区五校联考2022-2023学年九年级下学期3月数学试题
试卷更新日期:2023-03-17 类型:月考试卷
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 下列几何体中,俯视图为三角形的是( )A、
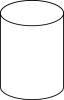 B、
B、 C、
C、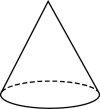 D、
D、 3. 中国移动数据中心IDC项目近日在高新区正式开工建设,该项目规划建设规模12.6万平方米,建成后将成为山东省最大的数据业务中心.其中126000用科学记数法表示应为( )A、1.26×106 B、12.6×104 C、0.126×106 D、1.26×1054.
3. 中国移动数据中心IDC项目近日在高新区正式开工建设,该项目规划建设规模12.6万平方米,建成后将成为山东省最大的数据业务中心.其中126000用科学记数法表示应为( )A、1.26×106 B、12.6×104 C、0.126×106 D、1.26×1054.如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )
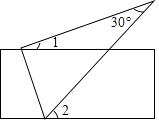 A、50° B、60° C、70° D、80°5. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
A、50° B、60° C、70° D、80°5. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、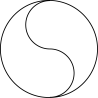 C、
C、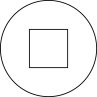 D、
D、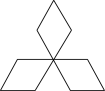 6. 下列运算中,计算正确的是( )A、 B、 C、 D、7. 若方程x2−cx+4=0有两个不相等的实数根,则c的值不可能是( )A、10 B、6 C、3 D、8. 若 , 则正比例函数与反比例函数在同一平面直角坐标系中的大致图像可能是( )A、
6. 下列运算中,计算正确的是( )A、 B、 C、 D、7. 若方程x2−cx+4=0有两个不相等的实数根,则c的值不可能是( )A、10 B、6 C、3 D、8. 若 , 则正比例函数与反比例函数在同一平面直角坐标系中的大致图像可能是( )A、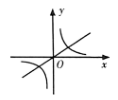 B、
B、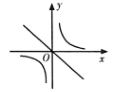 C、
C、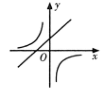 D、
D、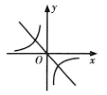 9. 如图,在矩形 按以下步骤作图:①分别以点A和C为圆心,以大于 的长为半径作弧,两弧相交于点M和N;②作直线 交 于点E;③连接 , .若 , ,则 的度数为( )
9. 如图,在矩形 按以下步骤作图:①分别以点A和C为圆心,以大于 的长为半径作弧,两弧相交于点M和N;②作直线 交 于点E;③连接 , .若 , ,则 的度数为( ) A、 B、 C、 D、10. 在平面直角坐标系中,对于点和点 , 给出如下新定义,若 , 则称点是点的限变点,例如:点的限变点是 , 点的限变点是 , 若点在二次函数的图象上,则当时,其限变点的纵坐标的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、10. 在平面直角坐标系中,对于点和点 , 给出如下新定义,若 , 则称点是点的限变点,例如:点的限变点是 , 点的限变点是 , 若点在二次函数的图象上,则当时,其限变点的纵坐标的取值范围是( )A、 B、 C、 D、二、填空题
-
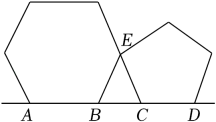
11. 分解因式: =12. 一个不透明的袋子中装有3个小球,其中2个红球,1个绿球,这些小球除颜色外无其他差别,从袋子中随机摸出一个小球,则摸出的小球是红球的概率为 .13. 方程的解为 .14. 如图,将一个正六边形与一个正五边形如图放置,顶点A、B、C、D四点共线,E为公共顶点.则∠BEC= .
 15. 小泽和小帅两同学分别从甲地出发,骑自行车沿同一条路到乙地参加社会实践活动.如图折线和线段分别表示小泽和小帅离甲地的距离y(单位:千米)与时间x(单位:小时)之间函数关系的图象,则当小帅到达乙地时,小泽距乙地的距离为千米.
15. 小泽和小帅两同学分别从甲地出发,骑自行车沿同一条路到乙地参加社会实践活动.如图折线和线段分别表示小泽和小帅离甲地的距离y(单位:千米)与时间x(单位:小时)之间函数关系的图象,则当小帅到达乙地时,小泽距乙地的距离为千米.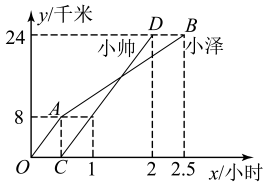 16. 如图,矩形纸片 , , 点E,F分别在 , 上,把纸片如图沿折叠,点A,B的对应点分别为 , , 连接并延长交线段于点G,则的值为 .
16. 如图,矩形纸片 , , 点E,F分别在 , 上,把纸片如图沿折叠,点A,B的对应点分别为 , , 连接并延长交线段于点G,则的值为 .
三、解答题
-
17. 计算: .18. 解不等式组: , 并写出它的正整数解.19. 如图,点E是正方形内一点,是等边三角形,连接 . 求证: .
 20. 某校为调查学生对海洋科普知识的了解情况,从全校学生中随机抽取n名学生进行测试,测试成绩进行整理后分成五组,并绘制成如图的频数分布直方图和扇形统计图.
20. 某校为调查学生对海洋科普知识的了解情况,从全校学生中随机抽取n名学生进行测试,测试成绩进行整理后分成五组,并绘制成如图的频数分布直方图和扇形统计图.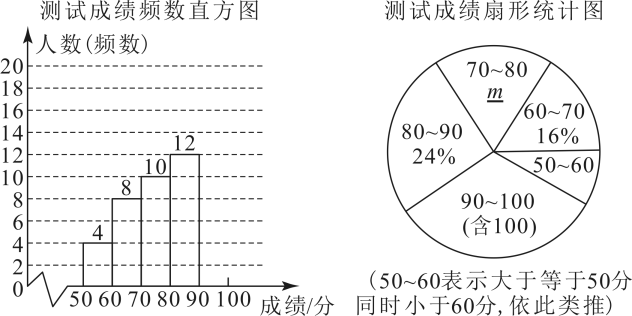
请根据图中信息解答下列问题:
(1)、补全频数分布直方图;(2)、在扇形统计图中,“”这组的百分比m=;(3)、已知“”这组的数据如下:83,85,87,81,86,84,88,85,86,86,88,89.这组数据的众数是分;抽取的n名学生测试成绩的中位数是分;(4)、若成绩达到80分以上(含80分)为优秀,请你估计全校1200名学生对海洋科普知识了解情况为优秀的学生人数.21. 如图,为的直径,切于E,于C,交于D.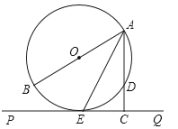 (1)、求证:平分;(2)、若 , , 求的半径.22. 某学校教学楼(甲楼)的顶部E和大门A之间挂了一些彩旗.小颖测得大门A距甲楼的距离是 , 在A处测得甲楼顶部E处的仰角是31°.
(1)、求证:平分;(2)、若 , , 求的半径.22. 某学校教学楼(甲楼)的顶部E和大门A之间挂了一些彩旗.小颖测得大门A距甲楼的距离是 , 在A处测得甲楼顶部E处的仰角是31°.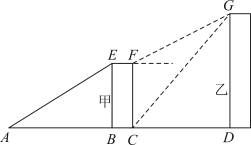 (1)、求甲楼的高度;(2)、若小颖在甲楼楼底C处测得学校后面医院楼(乙楼)楼顶G处的仰角为 , 爬到甲楼楼顶F处测得乙楼楼顶G处的仰角为 , 求甲乙两楼之间的距离.(结果带根号)( . . )23. 2022年10月16日,习总书记在第二十次全国代表大会上的报告中提出:“积极稳妥推进碳达峰碳中和”.某公司积极响应节能减排号召,决定采购新能源A型和B型两款汽车,已知每辆A型汽车的进价是每辆B型汽车的进价的1.5倍,若用3000万元购进A型汽车的数量比2400万元购进B型汽车的数量少20辆.(1)、A型和B型汽车的进价分别为每辆多少万元?(2)、该公司决定用不多于3600万元购进A型和B型汽车共150辆,最多可以购买多少辆A型汽车?24. 正方形的边长为4, , 交于点E.在点A处建立平面直角坐标系如图所示.
(1)、求甲楼的高度;(2)、若小颖在甲楼楼底C处测得学校后面医院楼(乙楼)楼顶G处的仰角为 , 爬到甲楼楼顶F处测得乙楼楼顶G处的仰角为 , 求甲乙两楼之间的距离.(结果带根号)( . . )23. 2022年10月16日,习总书记在第二十次全国代表大会上的报告中提出:“积极稳妥推进碳达峰碳中和”.某公司积极响应节能减排号召,决定采购新能源A型和B型两款汽车,已知每辆A型汽车的进价是每辆B型汽车的进价的1.5倍,若用3000万元购进A型汽车的数量比2400万元购进B型汽车的数量少20辆.(1)、A型和B型汽车的进价分别为每辆多少万元?(2)、该公司决定用不多于3600万元购进A型和B型汽车共150辆,最多可以购买多少辆A型汽车?24. 正方形的边长为4, , 交于点E.在点A处建立平面直角坐标系如图所示.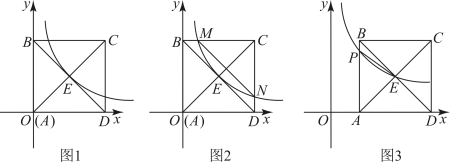 (1)、如图(1),双曲线过点E,完成填空:点C的坐标是 . 点E的坐标是 , 双曲线的解析式是;(2)、如图(2),双曲线与 , 分别交于点M,N(反比例图像不一定过点E).求证;(3)、如图(3),将正方形向右平移个单位长度,使过点E的双曲线与交于点P.当是以为腰的等腰三角形时,求m的值.25.
(1)、如图(1),双曲线过点E,完成填空:点C的坐标是 . 点E的坐标是 , 双曲线的解析式是;(2)、如图(2),双曲线与 , 分别交于点M,N(反比例图像不一定过点E).求证;(3)、如图(3),将正方形向右平移个单位长度,使过点E的双曲线与交于点P.当是以为腰的等腰三角形时,求m的值.25.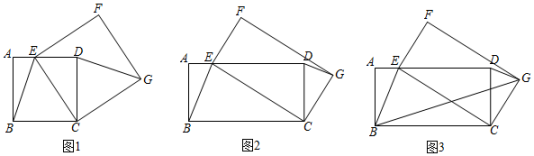 (1)、【问题情境】如图1,四边形ABCD是正方形,点E是AD边上的一个动点,以CE为边在CE的右侧作正方形CEFG,连接DG、BE,则DG与BE的数量关系是;(2)、【类比探究】
(1)、【问题情境】如图1,四边形ABCD是正方形,点E是AD边上的一个动点,以CE为边在CE的右侧作正方形CEFG,连接DG、BE,则DG与BE的数量关系是;(2)、【类比探究】如图2,四边形ABCD是矩形,AB=2,BC=4,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE.判断线段DG与BE有怎样的数量关系和位置关系,并说明理由;
(3)、【拓展提升】如图3,在(2)的条件下,连接BG,则2BG+BE的最小值为 .
26. 抛物线过 , , 三点.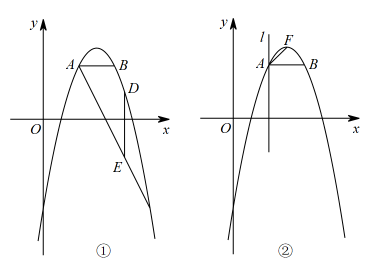 (1)、求抛物线的表达式;(2)、如图①,点K与点C关于抛物线对称轴对称,抛物线上一点D在线段AK的上方,交AK于点E,若满足 , 求点D的坐标;(3)、如图②,F为抛物线顶点,过A作直线 , 若点P在直线l上运动,点Q在x轴上运动.是否存在这样的点P、Q,使得与相似(P与F为对应点),若存在,直接写出P、Q的坐标及此时的面积;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、如图①,点K与点C关于抛物线对称轴对称,抛物线上一点D在线段AK的上方,交AK于点E,若满足 , 求点D的坐标;(3)、如图②,F为抛物线顶点,过A作直线 , 若点P在直线l上运动,点Q在x轴上运动.是否存在这样的点P、Q,使得与相似(P与F为对应点),若存在,直接写出P、Q的坐标及此时的面积;若不存在,请说明理由.