上海市虹口区2023年九年级中考一模数学试卷
试卷更新日期:2023-03-17 类型:中考模拟
一、单选题
-
1. 如果某个斜坡的坡度是 , 那么这个斜坡的坡角为( )A、30° B、45° C、60° D、90°2. 如图,在中, , 那么的值为( )
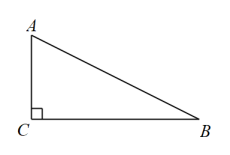 A、 B、2 C、 D、3. 已知抛物线有最低点,那么a的取值范围是( )A、 B、 C、 D、4. 已知二次函数的图像如图所示,那么下列四个结论中,错误的是( )
A、 B、2 C、 D、3. 已知抛物线有最低点,那么a的取值范围是( )A、 B、 C、 D、4. 已知二次函数的图像如图所示,那么下列四个结论中,错误的是( )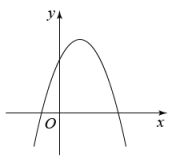 A、 B、 C、 D、5. 如果点与点都在抛物线上,那么和的大小关系是( )A、 B、 C、 D、不能确定6. 如图,点分别在Δ边上, , 且 , 那么的值为( )
A、 B、 C、 D、5. 如果点与点都在抛物线上,那么和的大小关系是( )A、 B、 C、 D、不能确定6. 如图,点分别在Δ边上, , 且 , 那么的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 已知线段b是线段a、c的比例中项,且 , , 那么b= .8. 计算: .9. 抛物线与y轴的交点坐标是 .10. 沿着x轴正方向看,抛物线在其对称轴右侧的部分是的.(填“上升”或“下降”)11. 在平面直角坐标系中,将抛物线沿着y轴向下平移2个单位,所得到的新抛物线的表达式为 .12. 已知抛物线上部分点的横坐标x与纵坐标y的对应值如下表:
…
0
2
3
4
…
…
5
2
2
5
10
…
如果点在此抛物线上,那么m= .
13. 已知 , 顶点分别与对应, , 的平分线的长为6,那么的平分线的长为 .14. 如图,在中,点D在边上,已知和的面积比是 , , , 那么用向量表示向量为 . 15. 如图,在梯形中, , 点分别在边上且 , 已知 , , 那么的长是 .
15. 如图,在梯形中, , 点分别在边上且 , 已知 , , 那么的长是 . 16. 如图,在中, , 点G为的重心,过点G作交于点D.已知 , 那么的长为 .
16. 如图,在中, , 点G为的重心,过点G作交于点D.已知 , 那么的长为 . 17. 魏晋时期,数学家刘徽利用如图所示的“青朱出入图”证明了勾股定理,其中四边形、四边形和四边形都是正方形.如果图中与的面积比为 , 那么的值为 .
17. 魏晋时期,数学家刘徽利用如图所示的“青朱出入图”证明了勾股定理,其中四边形、四边形和四边形都是正方形.如果图中与的面积比为 , 那么的值为 . 18. 我们规定:如果一个三角形一边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.如图,已知直线 , 与之间的距离是3,“等高底”的“等底”在直线上(点B在点C的左侧),点A在直线上, , 将绕点B顺时针旋转得到 , 点的对应点分别为点 , 那么的长为 .
18. 我们规定:如果一个三角形一边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.如图,已知直线 , 与之间的距离是3,“等高底”的“等底”在直线上(点B在点C的左侧),点A在直线上, , 将绕点B顺时针旋转得到 , 点的对应点分别为点 , 那么的长为 .
三、解答题
-
19. 计算:cos245° +cot230°.20. 如图,在平面直角坐标系中,抛物线与x轴交于点和 , 与y轴交于点C.
 (1)、求此抛物线的表达式及点C的坐标;(2)、将此抛物线沿x轴向左平移个单位得到新抛物线,且新抛物线仍经过点C,求m的值.21. 如图,在中, , 点E在边上,且 , 过点E作交边于点D,的平分线交线段于点F,求的长.
(1)、求此抛物线的表达式及点C的坐标;(2)、将此抛物线沿x轴向左平移个单位得到新抛物线,且新抛物线仍经过点C,求m的值.21. 如图,在中, , 点E在边上,且 , 过点E作交边于点D,的平分线交线段于点F,求的长.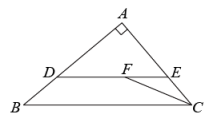 22. 如图1是钢琴缓降器,图2和图3是钢琴缓降器两个位置的示意图.是缓降器的底板,压柄可以绕着点B旋转,液压伸缩连接杆的端点分别固定在压柄与底板上,已知 .
22. 如图1是钢琴缓降器,图2和图3是钢琴缓降器两个位置的示意图.是缓降器的底板,压柄可以绕着点B旋转,液压伸缩连接杆的端点分别固定在压柄与底板上,已知 .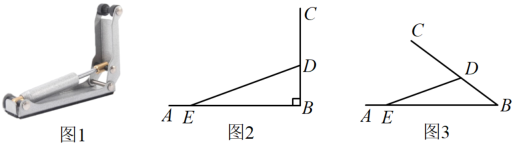 (1)、如图2,当压柄与底座垂直时,约为 , 求的长;(2)、现将压柄从图2的位置旋转到与成角(即),如图3的所示,求此时液压伸缩连接杆的长.(结果保留根号)
(1)、如图2,当压柄与底座垂直时,约为 , 求的长;(2)、现将压柄从图2的位置旋转到与成角(即),如图3的所示,求此时液压伸缩连接杆的长.(结果保留根号)(参考数据:;)
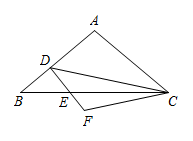
23. 如图,在四边形中,对角线与交于点F, . (1)、求证:;(2)、过点A作交于点E,求证: .
(1)、求证:;(2)、过点A作交于点E,求证: .