上海市徐汇区2023年中考一模数学试卷

试卷更新日期：2023-03-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 在 $R t △ A B C$ 中， $∠ C = 90 ° ， A B = 5 ， A C = 4$ ．下列四个选项，正确的是（）

A、 $t a n B = \frac{3}{4}$ B、 $c o t B = \frac{4}{3}$ C、 $s i n B = \frac{4}{5}$ D、 $c o s B = \frac{4}{5}$

查看试题解析
2. 下列命题中假命题是（）

A、任意两个等腰直角三角形都相似 B、任意两个含36°内角的等腰三角形相似 C、任意两个等边三角形都相似 D、任意两个直角边之比为1：2的直角三角形相似

查看试题解析
3. 如图， $a ∥ b ∥ c$ ，若 $\frac{A D}{D F} = \frac{3}{2}$ ，则下面结论错误的是（）

A、 $\frac{A D}{A F} = \frac{3}{5}$ B、 $\frac{B C}{C E} = \frac{3}{2}$ C、 $\frac{A B}{E F} = \frac{2}{3}$ D、 $\frac{B C}{B E} = \frac{3}{5}$

查看试题解析
4. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图像如图所示，点P在x轴的正半轴上，且 $O P = 1$ ，下列选项中正确的是（）

A、 $a > 0$ B、 $c < 0$ C、 $a + b + c > 0$ D、 $b < 0$

查看试题解析
5. 将抛物线 $y = - \frac{1}{2} x^{2}$ 经过下列平移能得到抛物线 $y = - \frac{1}{2} {(x + 1)}^{2} - 3$ 的是（）

A、向右 $1$ 个单位，向下 $3$ 个单位 B、向左 $1$ 个单位，向下 $3$ 个单位 C、向右 $1$ 个单位，向上 $3$ 个单位 D、向左 $1$ 个单位，向上 $3$ 个单位

查看试题解析
6. 如图，点D在 $△ A B C$ 边 $A B$ 上， $∠ A C D = ∠ B$ ，点F是 $△ A B C$ 的角平分线 $A E$ 与 $C D$ 的交点，且 $A F = 2 E F$ ，则下列选项中错误的是（）

A、 $\frac{A D}{A C} = \frac{2}{3}$ B、 $\frac{C F}{B E} = \frac{2}{3}$ C、 $\frac{D C}{B C} = \frac{2}{3}$ D、 $\frac{A D}{D B} = \frac{2}{3}$

查看试题解析

二、填空题

7. 已知 $\frac{x}{y} = \frac{4}{3}$ ，则 $\frac{x - y}{x + y} =$ ．

查看试题解析
8. 计算： $2 (\vec{a} - \vec{b}) - \frac{1}{3} (3 \vec{a} - \vec{b}) =$ ．

查看试题解析
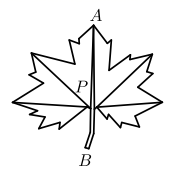
9. 两个相似三角形的对应边上的中线之比 $4 ： 5$ ，则这两个三角形面积之比为．

查看试题解析
10. 大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”.如图， $P$ 为 $A B$ 的黄金分割点 $(A P > P B)$ ，如果 $A B$ 的长度为 $8 c m$ ，那么 $A P$ 的长度是.

查看试题解析
11. 如图，已知G为 $Δ A B C$ 的重心，过点G作 $B C$ 的平行线交边 $A B$ 和 $A C$ 于点D、E，设 $\vec{G B} = \vec{a}$ 、 $\vec{G C} = \vec{b}$ ．用 $x \vec{a} + y \vec{b}$ （ $x 、 y$ 为实数）的形式表示向量 $\vec{D E} =$ ．

查看试题解析
12. 小明和小杰去公园游玩，小明给站在观景台边缘的小杰拍照时，发现他的眼睛、凉亭顶端、小杰的头顶三点恰好在一条直线上（如图所示）．已知小明的眼睛离地面的距离 $A B$ 为 $1.6$ 米，凉亭的高度 $C D$ 为 $6.6$ 米，小明到凉亭的距离 $B D$ 为 $12$ 米，凉亭与观景台底部的距离 $D F$ 为 $42$ 米，小杰身高为 $1.8$ 米．那么观景台的高度为米．

查看试题解析
13. 已知点 $A (- 3 ， m)$ 、 $B (- 2 ， n)$ 在抛物线 $y = - x^{2} - 2 x + 4$ 上，则mn（填“>”、“=”或“<”）．

查看试题解析
14. 小球沿着坡度为 $i = 1 ： 1.5$ 的坡面滚动了 $13 m$ ，则在这期间小球滚动的水平距离是m．

查看试题解析
15. 计算： $\frac{c o s 60 ° - s i n 60 °}{c o t 30 ° - t a n 45 °} =$

查看试题解析
16. 如图，在由正三角形构成的网格图中， $A 、 B 、 C$ 三点均在格点上，则 $s i n ∠ B A C$ 的值为．

查看试题解析
17. 如图，点E是矩形 $A B C D$ 纸片边 $C D$ 上一点，如果沿着 $A E$ 折叠矩形纸片，恰好使点D落在边 $B C$ 上的点F处，已知 $B F = 6 c m ， t a n ∠ B A F = \frac{3}{4}$ ，那么折痕 $A E$ 的长是 $c m$ ．

查看试题解析
18. 规定：如果经过三角形一个顶点的直线把这个三角形分成两个小三角形，其中一个小三角形是等腰三角形，另一个小三角形和原三角形相似，那么符合这样条件的三角形称为“和谐三角形”，这条直线称为这个三角形的“和谐分割线”．例如，如图所示，在 $R t △ A B C$ 中， $∠ C = 90 ° ， C A = C B$ ， $C D$ 是斜边 $A B$ 上的高，其中 $△ A C D$ 是等腰三角形，且 $△ B C D$ 和 $△ A B C$ 相似，所以 $△ A B C$ 是“和谐三角形”，直线 $C D$ 为 $△ A B C$ 的“和谐分割线”．请依据规定求解问题：已知 $△ D E F$ 是“和谐三角形”， $∠ D = 42 °$ ，当直线 $E G$ 是 $△ D E F$ 的“和谐分割线”时， $∠ F$ 的度数是（写出所有符合条件的情况）

查看试题解析

三、解答题

19. 如图，在 $△ A B C$ 中，已知 $∠ C = 90 ° ， s i n A = \frac{5}{13}$ ．点 $D$ 为边 $A C$ 上一点， $∠ B D C = 45 ° ， A D = 7$ ，求 $C D$ 的长．

查看试题解析
20. 如图，点E在平行四边形 $A B C D$ 的边 $B C$ 的延长线上，且 $C E = 2 B C$ ， $A E$ 与 $C D$ 交于点F．设 $\vec{A B} = \vec{a} ， \vec{A D} = \vec{b}$ ．

(1)、用向量 $\vec{a}$ 、 $\vec{b}$ 表示向量 $\vec{D E}$ ；

(2)、求作：向量 $\vec{E F}$ 分别在向量 $\vec{E C}$ 、 $\vec{E D}$ 方向上的分向量．（不要求写作法，但要保留作图痕迹，并指出所作图中表示结论的分向量）

查看试题解析
21. 已知二次函数 $y = - 3 x^{2} + 6 x + 9$ ．

(1)、用配方法把二次函数 $y = - 3 x^{2} + 6 x + 9$ 化为 $y = a {(x + m)}^{2} + k$ 的形式，并指出这个函数图象的开口方向、对称轴和顶点的坐标；

(2)、如果将该函数图象向右平移2个单位，所得的新函数的图象与x轴交于点 $A 、 B$ （点A在点B左侧），与y轴交于点C，顶点为D，求四边形 $D A C B$ 的面积．

查看试题解析
22. 如图，是一个放置于水平桌面的平板支架的示意图，底座的高 $A B$ 为 $5 c m$ ，宽 $M N$ 为 $10 c m$ ，点A是 $M N$ 的中点，连杆 $B C 、 C D$ 的长度分别为 $18.5 c m$ 和 $15 c m$ ， $∠ C B A = 150 °$ ，且连杆 $B C 、 C D$ 与 $A B$ 始终在同一平面内．

(1)、求点C到水平桌面的距离；

(2)、产品说明书提示，若点D与A的水平距离超过 $A N$ 的长度，则该支架会倾倒．现将 $∠ D C B$ 调节为 $80 °$ ，此时支架会倾倒吗？（参考数据∶ $t a n 20 ° \approx 0.36 ， c o t 20 ° \approx 2.75 ， s i n 20 ° \approx 0.34 ， c o s 20 ° \approx 0.94$ ）

查看试题解析
23. 如图，已知 $△ A B C$ 是等边三角形， $D 、 E$ 分别是边 $B C 、 A C$ 上的点，且 $B C \cdot C E = B D \cdot D C$ ．在 $D E$ 的延长线上取点F，使得 $D F = A D$ ，联结 $C F$ ．

(1)、求证： $∠ A D E = 60 °$ ；

(2)、求证： $C F ∥ A B$ ．

查看试题解析
24. 已知在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} + b x + 3$ 经过点 $A (- 1 ， 0)$ 、 $B (4 ， 0)$ 与y轴相交于点C．

(1)、求抛物线的表达式；

(2)、点P是第一象限内抛物线上的一个动点，过点P作直线 $P D ⊥ x$ 轴，垂足为点D，直线 $P D$ 与直线 $B C$ 相交于点E．
①当 $C P = C E$ 时，求点P的坐标；
②联结 $A C$ ，过点P作直线 $A C$ 的平行线，交x轴于点F，当 $∠ B P F = ∠ C B A$ 时，求点P的坐标．

查看试题解析
25. 如图1，已知菱形 $A B C D$ ，点E在边 $B C$ 上， $∠ B F E = ∠ A B C$ ， $A E$ 交对角线 $B D$ 于点F．

(1)、求证 $△ A B F ∽ △ D B A$ ；

(2)、如图2，联结 $C F$ ．
①当 $△ C E F$ 为直角三角形时，求 $∠ A B C$ 的大小；
②如图3，联结 $D E$ ，当 $D E ⊥ F C$ 时，求 $c o s ∠ A B D$ 的值．

查看试题解析