上海市金山区2023年中考一模数学试卷

试卷更新日期：2023-03-17 类型：中考模拟

进入出卷网下载

一、单选题

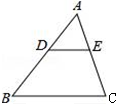
1. 下列 $y$ 关于 $x$ 的函数中，属于二次函数的是（）

A、 $y = 2 x + 1$ B、 $y = \frac{2}{x}$ C、 $y = 3 x^{2} + 1$ D、 $y = \sqrt{x^{2} + 1}$

查看试题解析
2. 下列各组中的四条线段成比例的是（）

A、 $1 c m 、 2 c m 、 3 c m 、 4 c m$ B、 $2 c m 、 3 c m 、 4 c m 、 5 c m$ C、 $3 c m 、 4 c m 、 6 c m 、 9 c m$ D、 $2 c m 、 3 c m 、 4 c m 、 6 c m$

查看试题解析
3. 在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，tanB＝（）

A、 $\frac{4}{5}$ B、 $\frac{3}{4}$ C、 $\frac{3}{5}$ D、 $\frac{4}{3}$

查看试题解析
4. 在△ABC中，点D、E分别在边AB、AC上，如果AD＝2，BD＝4，那么由下列条件能够判断DE∥BC的是（）

A、 $\frac{AE}{AC}$ ＝ $\frac{1}{2}$ B、 $\frac{DE}{BC}$ ＝ $\frac{1}{3}$ C、 $\frac{AE}{AC}$ ＝ $\frac{1}{3}$ D、 $\frac{DE}{BC}$ ＝ $\frac{1}{2}$

查看试题解析
5. 已知 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ 是非零问量，下列条件中不能判定 $\vec{a}$ $∥$ $\vec{b}$ 的是（）

A、 $\vec{a}$ $∥$ $\vec{c}$ ， $\vec{b}$ $∥$ $\vec{c}$ B、 $\vec{a} = 3 \vec{b}$ C、 $| \vec{a} | = | \vec{b} |$ D、 $\vec{a} = \frac{1}{2} \vec{c}$ ， $\vec{b} = - 2 \vec{c}$

查看试题解析
6. 如图，已知抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与x轴交于A、B两点，与y轴交于点C，对称轴直线 $x = 1$ 与x轴交于点D，若 $O A < O D$ ，那么下列判断正确的是（）

A、 $a + b + c < 0$ B、 $a - b + c > 0$ C、 $2 a + b + c < 0$ D、 $9 a + 3 b + c < 0$

查看试题解析

二、填空题

7. 已知 $\frac{a}{b} = \frac{4}{3}$ ，则 $\frac{a - b}{b} =$ ．

查看试题解析
8. 已知 $f (x) = x^{2} - 2 x + 3$ ，那么 $f (2) =$ ．

查看试题解析
9. 已知 $α$ 是锐角，且 $c o s α = \frac{\sqrt{2}}{2}$ ，那么 $α =$ ．

查看试题解析
10. 将抛物线 $y = 2 (x + 4)^{2}$ 向右平移3个单位，得到新抛物线的表达式是．

查看试题解析
11. 抛物线 $y = (k + 2) x^{2} - 3 x - 1$ 有最高点，那么k的取值范围是．

查看试题解析
12. 如图，已知上海东方明珠电视塔塔尖A到地面底部B的距离是468米，第二球体点P处恰好是整个塔高的一个黄金分割点（点A、B、P在一直线），且 $B P > A P$ ，那么底部B到球体P之间的距离是米（结果保留根号）

查看试题解析
13. 某商场营业厅自动扶梯的示意图如图所示，自动扶梯 $A B$ 坡度 $i = 1 ： \sqrt{3}$ ，自动扶梯 $A B$ 的长度为12米，那么大厅两层之间的高度BC=米．

查看试题解析
14. 如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，tan∠DCB＝ $\frac{3}{4}$ ， AC＝12，则BC= ．

查看试题解析
15. 如图， $A B$ 与 $C D$ 相交于点E， $A C ∥ B D$ ，联结 $B C$ ，若 $A E = 2 ， B E = 3$ ，设 $\vec{A C} = \vec{a}$ ， $\vec{E D} = \vec{b}$ ，那么 $\vec{B C} =$ （用含 $\vec{a} 、 \vec{b}$ 的式子表示）

查看试题解析
16. 如图，在平行四边形 $A B C D$ 中，F是边 $A D$ 上的一点，射线 $C F$ 和 $B A$ 的延长线交于点E，如果 $C_{△ E A F} ： C_{△ C D F} = 1 ： 2$ ，那么 $S_{△ E A F} ： S_{四边形 A B C F} =$ ．

查看试题解析
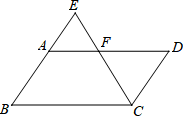17. 我们把将一个三角形面积分为相等的两个部分的直线称为美丽线．如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，直线 $D E$ 是 $R t △ A B C$ 的一条美丽线，直线 $D E$ 分别交边 $A B 、 B C$ 于点D、E，交 $A C$ 延长线于点F，当 $D E ⊥ A B ， B D = 2 A D$ 时，那么 $c o s F$ 的值为．

查看试题解析
18. 如图， $△ A B C$ 为等腰直角三角形， $∠ A = 90 ° ， A B = 6 ， G_{1}$ 为 $△ A B C$ 的重心，E为线段 $A B$ 上任意一动点，以 $C E$ 为斜边作等腰 $R t △ C D E$ （点D在直线 $B C$ 的上方）， $G_{2}$ 为 $R t △ C D E$ 的重心，设 $G_{1} 、 G_{2}$ 两点的距离为d，那么在点E运动过程中d的取值范围是．

查看试题解析

三、解答题

19. 计算： $\frac{4 s i n^{2} 45 ° - t a n 45 °}{2 c o s 60 °} + 2 c o t 30 ° \cdot s i n 60 °$ ．

查看试题解析
20. 如图，已知抛物线 $y = a (x - 2)^{2} - 4 (a \neq 0)$ 与x轴交于原点O与点A，顶点为点B．

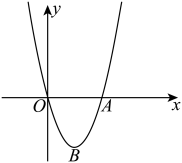(1)、求抛物线的表达式以及点A的坐标；

(2)、已知点 $P (2 ， m) (m > 0)$ ，若 $△ P A B$ 的面积为6，求点P的坐标．

查看试题解析
21. 如图，已知在四边形 $A B C D$ 中， $A D ∥ B C ， ∠ A = 90 ° ， A D = 2 ， B C = 6 ， B D$ 是对角线， $B D ⊥ D C$ ．

(1)、求证： $△ A B D ∽ △ D C B$ ；

(2)、求 $C D$ 的长．

查看试题解析
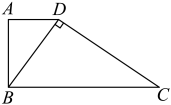22. 如图，小睿为测量公园的一凉亭 $A B$ 的高度，他先在水平地面点E处用高 $1.5 m$ 的测角仪 $D E$ 测得顶部A的仰角为 $31 °$ ，然后沿 $E B$ 方向向前走 $3 m$ 到达点G处，在点G处用高 $1.5 m$ 的测角仪 $F G$ 测得顶部A的仰角为 $42 °$ ．求凉亭 $A B$ 的高度（ $A B ⊥ B E ， D E ⊥ B E ， F G ⊥ B E$ ，结果精确到 $0.1 m$ ）．
（参考数据： $s i n 31 ° ≈ 0.52$ ， $c o s 31 ° ≈ 0.86$ ， $t a n 31 ° \approx 0.60$ ， $s i n 42 ° \approx 0.67$ ， $c o s 42 ° \approx 0.74$ ， $t a n 42 ° \approx 0.90$ ）

查看试题解析
23. 如图，已知菱形 $A B C D$ 中，点E在边 $C B$ 延长线上，联结 $D E$ 交边 $A B$ 于点F，联结 $A E$ ，过点F作 $F G ∥ B E$ 交 $A E$ 于点G．

(1)、求证： $F G = B F$ ；

(2)、联结 $A C$ 交 $D E$ 于点O，联结 $B O$ ，当 $∠ F O B = ∠ D A O$ 时，求证： $D O^{2} = A B \cdot G F$ ．

查看试题解析
24. 已知抛物线 $y = a x^{2} + b x - 3$ 经过点 $A (1 ， 0)$ ， $B (- 2 ， - 3)$ ，顶点为点P，与y轴交于点C．

(1)、求该抛物线的表达式以及顶点P的坐标；

(2)、将抛物线向上平移 $m (m > 0)$ 个单位后，点A的对应点为点M，若此时 $M B ∥ A C$ ，求m的值；

(3)、设点D在抛物线 $y = a x^{2} + b x - 3$ 上，且点D在直线 $B C$ 上方，当 $∠ D B C = ∠ B A C$ 时，求点D的坐标．

查看试题解析
25. 已知平行四边形 $A B C D$ 中， $A B = 3 \sqrt{5} ， t a n ∠ A B C = 2 ， B C = 5$ ，点P是对角线 $B D$ 上一动点，作 $∠ E P D = ∠ A B C$ ，射线 $P E$ 交射线 $B A$ 于点E，联结 $A P$ ．

(1)、如图1，当点E与点A重合时，证明： $△ A B P ∽ △ B C D$ ；

(2)、如图2，点E在 $B A$ 的延长线上，当 $E P = A D$ 时，求 $A E$ 的长；

(3)、当 $△ A P E$ 是以 $A P$ 为底的等腰三角形时，求 $A E$ 的长．

查看试题解析