上海市奉贤区2023年中考数学一模试卷

试卷更新日期：2023-03-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列函数中，函数值y随自变量x的值增大而减小的是（）

A、 $y = \frac{x}{2}$ B、 $y = - \frac{x}{2}$ C、 $y = \frac{2}{x}$ D、 $y = - \frac{2}{x}$

查看试题解析
2. 已知抛物线 $y = x^{2} - 3$ ，如果点 $A (1 ， - 2)$ 与点B关于该抛物线的对称轴对称，那么点B的坐标是（）

A、 $(2 ， 1)$ B、 $(- 2 ， - 1)$ C、 $(1 ， 2)$ D、 $(- 1 ， - 2)$

查看试题解析
3. 在 $△ A B C$ 中，点D、E分别在边AB、AC上，下列条件不能判定 $D E ∥ B C$ 的是（）

A、 $\frac{A D}{B D} = \frac{A E}{C E}$ B、 $\frac{A D}{A B} = \frac{A E}{A C}$ C、 $\frac{D E}{B C} = \frac{A D}{B D}$ D、 $\frac{B D}{A B} = \frac{C E}{A C}$

查看试题解析
4. 如果C是线段 $A B$ 的中点，那么下列结论中正确的是（）

A、 $\vec{A C} = \vec{B C}$ B、 $\vec{A C} ∥ \vec{B C}$ C、 $\vec{A C} + \vec{B C} = 0$ D、 $\vec{A B} = 2 \vec{B C}$

查看试题解析
5. 在直角坐标平面内有一点 $A (3 ， 1)$ ，设 $O A$ 与x轴正半轴的夹角为 $α$ ，那么下各式正确的是（）

A、 $s i n α = \frac{1}{3}$ B、 $c o s α = \frac{1}{3}$ C、 $t a n α = \frac{1}{3}$ D、 $c o t α = \frac{1}{3}$

查看试题解析
6. 如图，以 $A B$ 为斜边作等腰直角三角形 $A B C$ ，再以A为圆心， $A C$ 长为半径作弧，交线段 $A B$ 于点P，那么 $A P ： A B$ 等于（）

A、 $1 ： \sqrt{2}$ B、 $1 ： \sqrt{3}$ C、 $\sqrt{2} ： \sqrt{3}$ D、 $2 ： 3$

查看试题解析

二、填空题

7. 已知线段a＝4，b＝16，线段c是a，b的比例中项，那么c等于．

查看试题解析
8. 已知 $f (x) = \frac{2}{x - 1}$ ，那么 $f (- 1)$ 的值是．

查看试题解析
9. 一次函数 $y = 3 x + 1$ 的图像不经过的象限是．

查看试题解析
10. 如果两个等边三角形的边长的比是 $1 ： 4$ ，那么它们的周长比是．

查看试题解析
11. 如图2，已知 $A B ∥ C D ∥ E F$ ，它们依次交直线 $l_{1}$ 、 $l_{2}$ 于点A、C、E和点B、D、F．如果 $A C = 2$ ， $A E = 6$ ， $D F = 3$ ，那么 $B D =$ ．

查看试题解析
12. 在 $△ A B C$ 中，如果 $A B = A C = 7$ ， $B C = 10$ ，那么 $c o s B$ 的值是．

查看试题解析
13. 在 $△ A B C$ 中， $A D$ 是 $B C$ 边上的中线，G是重心．如果 $A D = 6$ ，那么线段 $D G$ 的长是．

查看试题解析
14. 如图，在 $△ A B C$ 中，点D、E、F分别在边 $A B$ 、 $A C$ 、 $B C$ 上， $D E ∥ B C$ ， $E F ∥ A B$ ，如果 $D E ： B C = 2 ： 5$ ，那么 $E F ： A B$ 的值是．

查看试题解析
15. 如图，在梯形 $A B C D$ 中， $A D ∥ B C$ ， $A C$ 与 $B D$ 相交于点O，如果 $B C ： A D = 3 ： 2$ ，那么 $S_{△ A D C} ： S_{△ A B C}$ 的值为．

查看试题解析
16. 已知一斜坡的坡度 $i = 1 ： 3$ ，高度为20米，那么这一斜坡的坡长约米．

查看试题解析
17. 如图，在△ABC中，∠ABC＝90°，∠A＝60°，直尺的一边与BC重合，另一边分别交AB，AC于点D，E．点B，C，D，E处的读数分别为15，12，0，1，则直尺宽BD的长为．

查看试题解析
18. 我们知道四边形具有不稳定性，容易变形（给定四边形各边的长，其形状和大小不确定）．如图，一个矩形发生变形后成为一个平行四边形，设这个平行四边形中较小的内角为 $α$ ，我们把 $s i n α$ 的值叫做这个平行四边形的“变形系数”．如果矩形的面积为 $5$ ，其变形后的平行四边形的面积为 $4$ ，那么这个平行四边形的“变形系数”是．

查看试题解析

三、解答题

19. 计算： $4 c o s 30 ° \cdot s i n 60 ° + \frac{1}{2 t a n 45 ° - c o t 30 °}$ ．

查看试题解析
20. 已知抛物线 $y = - x^{2} + 2 x + 3$ ，将这条抛物线向左平移3个单位，再向下平移2个单位．

(1)、求平移后新抛物线的表达式和它的开口方向、顶点坐标、对称轴，并说明它的变化情况；

(2)、在如图所示的平面直角坐标系内画出平移后的抛物线．

查看试题解析
21. 如图，在 $△ A B C$ 中，点D在边 $B C$ 上， $B D = A B = \frac{1}{2} B C$ ， E是 $B D$ 的中点．

(1)、求证： $∠ B A E = ∠ C$ ；

(2)、设 $\vec{A B} = \vec{a}$ ， $\vec{A D} = \vec{b}$ ，用向量 $\vec{a}$ 、 $\vec{b}$ 表示向量 $\vec{A C}$ ．

查看试题解析

22. 九（1）班同学在学习了“解直角三角形”的知识后，开展了“测量学校教学大楼高度”的活动中，在这个活动中他们设计了以下两种测量的方案：

课题	测量教学大楼的高度
方案	方案一	方案二
测量示意图
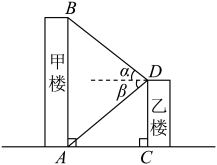
测得数据	甲楼和乙楼之间的距离 $A C = 20$ 米，乙楼顶端D测得甲楼顶端B的仰角 $α = 35 °$ ，测得甲楼底端A的俯角 $β = 40 °$	甲楼和乙楼之间的距离 $A C = 20$ 米，甲楼顶端B测得乙楼顶端D的俯角 $∠ F B D = 35 °$ ，测得乙楼底端C的俯角， $∠ F B C = 57 °$
参考数据	$s i n 35 ° \approx 0.57$ ， $s i n 40 ° \approx 0.64$ ， $s i n 57 ° \approx 0.84$ ， $c o s 35 ° \approx 0.82$ ， $c o s 40 ° \approx 0.77$ ， $c o s 57 ° \approx 0.54$ ， $t a n 35 ° \approx 0.70$ ， $t a n 40 ° \approx 0.84$ ， $t a n 57 ° \approx 1.53$ ．

请你选择其中一种方案，求甲楼和乙楼的高度．（结果精确到1米）

查看试题解析

23. 已知：如图，在梯形 $A B C D$ 中， $A D ∥ B C$ ，点E在对角线 $B D$ 上， $∠ E A D = ∠ B D C$ ．

(1)、求证： $A E \cdot B D = A D \cdot D C$ ；

(2)、如果点F在边DC上，且 $\frac{D F}{D E} = \frac{A E}{A D}$ ，求证： $E F ∥ B C$ ．

查看试题解析
24. 如图，在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} + b x + 3$ 的对称轴为直线 $x = 2$ ，顶点为A，与x轴分别交于点B和点C（点B在点C的左边），与y轴交于点D，其中点C的坐标为 $(3 ， 0)$ ．

(1)、求抛物线的表达式；

(2)、将抛物线向左或向右平移，将平移后抛物线的顶点记为E，联结DE．
①如果 $D E ∥ A C$ ，求四边形 $A C D E$ 的面积；
②如果点E在直线 $D C$ 上，点Q在平移后抛物线的对称轴上，当 $∠ D Q E = ∠ C D Q$ 时，求点Q的坐标．

查看试题解析
25. 如图，在平行四边形 $A B C D$ 中，点E在边 $A D$ 上， $C E$ 对角线 $B D$ 于点F， $∠ D C E = ∠ A D B$ ．

(1)、求证： $A B \cdot B C = B F \cdot C E$ ；

(2)、如果 $A D = 3 D E = 6$ ．
①求 $C F$ 的长；
②如果 $B D = 10$ ，求 $c o s ∠ A B C$ 值．

查看试题解析