上海市崇明区2023年中考一模数学试题
试卷更新日期:2023-03-17 类型:中考模拟
一、单选题
-
1. 下列各组图形中,一定相似的是( )A、两个矩形 B、两个菱形 C、两个正方形 D、两个等腰梯形2. 将函数的图像向右平移2个单位,下列结论中正确的是( )A、开口方向不变 B、顶点不变 C、对称轴不变 D、与轴的交点不变3. 在中, , 那么的值是( )A、 B、 C、 D、4. 已知为单位向量,向量与方向相反,且其模为的4倍;向量与方向相同,且其模为的2倍,则下列等式中成立的是( )A、 B、 C、 D、5. 四边形中,点F在边上,的延长线交的延长线于E点,下列式子中能判断的式子是( )
 A、 B、 C、 D、6. 如图,在中, , 垂足为点 , 以下条件中不能推出为直角三角形的是( )
A、 B、 C、 D、6. 如图,在中, , 垂足为点 , 以下条件中不能推出为直角三角形的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 若 , 且 , 则 .8. 计算: .9. 点P是线段的黄金分割点,如果 , 那么较长线段的长是 .10. 如果抛物线有最高点,那么m的取值范围是 .11. 如果抛物线的对称轴是y轴,那么它的顶点坐标为 .12. 已知点、为二次函数图像上的两点,那么 . (填“>”、“=”或“<”)13. 若两个相似三角形的周长比是4:9,则对应角平分线的比是 .14. 飞机离水平地面的高度为3千米,在飞机上测得该水平地面上的目标A点的俯角为 , 那么此时飞机与目标A点的距离为千米.(用的式子表示)15. 如图,在梯形中, , , , 则 .
 16. 如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么 =.
16. 如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么 =.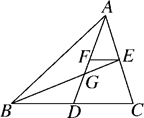 17. 如图,菱形的边长为8,E为的中点,平分交于点F,过点F作 , 交于点G,若 , 则的长为 .
17. 如图,菱形的边长为8,E为的中点,平分交于点F,过点F作 , 交于点G,若 , 则的长为 . 18. 如图,在中, , 点D在边上,点E在射线上,将沿翻折,使得点A落在点处,当且时,的长为 .
18. 如图,在中, , 点D在边上,点E在射线上,将沿翻折,使得点A落在点处,当且时,的长为 .
三、解答题
-
19. 计算:20. 如图,在梯形中, , 且 , 过点A作 , 分别交于点 , 若 .
 (1)、用表示和;(2)、求作在方向上的分向量.(不要求写作法,但要保留作图痕迹,并指出所作图中表示结论的分向量)21. 如图,D是边上的一点, , 垂足为点E,若 , .
(1)、用表示和;(2)、求作在方向上的分向量.(不要求写作法,但要保留作图痕迹,并指出所作图中表示结论的分向量)21. 如图,D是边上的一点, , 垂足为点E,若 , . (1)、求的长;(2)、若 , 求的值.22. 如图,一根灯杆上有一盏路灯A,路灯A离水平地面的高度为9米,在距离路灯正下方B点15.5米处有一坡度为的斜坡 , 如果高为3米的标尺竖立地面上,垂足为F,它的影子的长度为4米.
(1)、求的长;(2)、若 , 求的值.22. 如图,一根灯杆上有一盏路灯A,路灯A离水平地面的高度为9米,在距离路灯正下方B点15.5米处有一坡度为的斜坡 , 如果高为3米的标尺竖立地面上,垂足为F,它的影子的长度为4米. (1)、当影子全在水平地面上(图1),求标尺与路灯间的距离;(2)、当影子一部分在水平地面上,一部分在斜坡上(图2),求此时标尺与路灯间的距离为多少米?23. 已知:如图,在梯形中, , 对角线与交于点F,点G是边上的中点,连接交于点 , 并满足 .
(1)、当影子全在水平地面上(图1),求标尺与路灯间的距离;(2)、当影子一部分在水平地面上,一部分在斜坡上(图2),求此时标尺与路灯间的距离为多少米?23. 已知:如图,在梯形中, , 对角线与交于点F,点G是边上的中点,连接交于点 , 并满足 . (1)、求证:;(2)、求证:
(1)、求证:;(2)、求证:

