山东省青岛市市北区2023年一模数学试题
试卷更新日期:2023-03-17 类型:中考模拟
一、单选题
-
1. 下列实数是有理数的是( )A、 B、 C、0.121121112… D、2. 剪纸艺术是最古老的中国民间艺术之一,以下关于鱼的剪纸中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 我国古代数学家祖冲之推算出的近似值为 , 它与的误差小于0.0000003.将0.0000003用科学记数法可以表示为( )A、 B、 C、 D、4. 正在热映的春节档电影电影《满江红》中所使用的印信道具是中国悠久的金石文化的代表之一,它的表面均由正方形和等边三角形组成,可以看成图②所示的几何体,该几何体的主视图是( )
3. 我国古代数学家祖冲之推算出的近似值为 , 它与的误差小于0.0000003.将0.0000003用科学记数法可以表示为( )A、 B、 C、 D、4. 正在热映的春节档电影电影《满江红》中所使用的印信道具是中国悠久的金石文化的代表之一,它的表面均由正方形和等边三角形组成,可以看成图②所示的几何体,该几何体的主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,的顶点坐标分别为、、 , 线段交x轴于点P,如果将绕点P按顺时针方向旋转90°,得到 , 那么点B的对应点的坐标是( )
5. 如图,的顶点坐标分别为、、 , 线段交x轴于点P,如果将绕点P按顺时针方向旋转90°,得到 , 那么点B的对应点的坐标是( )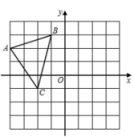 A、 B、 C、 D、6. 如图,四边形内接于 , , 平分交于点E,若 . 则的大小为( )
A、 B、 C、 D、6. 如图,四边形内接于 , , 平分交于点E,若 . 则的大小为( ) A、 B、 C、 D、7. 如图,在矩形中, , , 点E、F分别为、的中点,、相交于点G,过点E作 , 交于点H,则线段的长度是( )
A、 B、 C、 D、7. 如图,在矩形中, , , 点E、F分别为、的中点,、相交于点G,过点E作 , 交于点H,则线段的长度是( )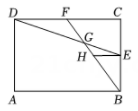 A、 B、1 C、 D、8. 如图,二次函数的图象与轴的一个交点为 , 对称轴为直线 . 则下列结论:
A、 B、1 C、 D、8. 如图,二次函数的图象与轴的一个交点为 , 对称轴为直线 . 则下列结论:①;②③④直线可能与有4个交点
⑤若点 , 点是抛物线上的两点,若 , 则 .
其中正确的有( )
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
9. 计算: .10. 已知关于x的一元二次方程有两个实数根,则k的取值范围是 .11. 如图,是甲、乙两人10次射击成绩(环数)的条形统计图,则甲、乙两人成绩较稳定的是;如果甲又连续射击了5次,且环数均为9环,那么甲的方差变化情况是(填“变大”“变小”或“不变”).
 12. 为预防“新冠病毒”,学校对教室喷洒消毒液(含氯消毒剂)进行消杀,资料表明空气中氯含量不低于 , 才能有效杀灭新冠病毒.如图,喷洒消毒液时教室空气中的氯含量与时间成正比例,消毒液挥发时,y与t成反比例,则此次消杀的有效作用时间是min.
12. 为预防“新冠病毒”,学校对教室喷洒消毒液(含氯消毒剂)进行消杀,资料表明空气中氯含量不低于 , 才能有效杀灭新冠病毒.如图,喷洒消毒液时教室空气中的氯含量与时间成正比例,消毒液挥发时,y与t成反比例,则此次消杀的有效作用时间是min. 13. 如图,在扇形中, , , 点C是上一动点,连接 , 过点A作于点D,连接 . 当的长度最小时,图中阴影部分的面积为 .
13. 如图,在扇形中, , , 点C是上一动点,连接 , 过点A作于点D,连接 . 当的长度最小时,图中阴影部分的面积为 . 14. 如图,已知矩形中, , , 点M,N分别在边 , 上,沿着折叠矩形 , 使点A,B分别落在E,F处,且点F在线段上(不与两端点重合),过点M作于点H,连接 , 给出下列判断:①;②折痕的长度的取值范围为;③当四边形为正方形时,为的中点;④若 , 则折叠后重叠部分的面积为 . 其中正确的是 . (写出所有正确判断的序号).
14. 如图,已知矩形中, , , 点M,N分别在边 , 上,沿着折叠矩形 , 使点A,B分别落在E,F处,且点F在线段上(不与两端点重合),过点M作于点H,连接 , 给出下列判断:①;②折痕的长度的取值范围为;③当四边形为正方形时,为的中点;④若 , 则折叠后重叠部分的面积为 . 其中正确的是 . (写出所有正确判断的序号).
三、解答题
-
15. 请用直尺、圆规作图,不写作法,但要保留作图痕迹.
求作:以点为直角顶点的等腰直角三角形,使它的斜边落在直线上,并在三角形内部做出以斜边中点为圆心的面积最大的半圆 .
 16.(1)、化简:(2)、解不等式组17. 由于疫情爆发,张明一家小区被管控,规定每两日每户可派一人出小区购买生活必需品.为增添生活乐趣,张明制作了下面两个可以自由转动的转盘:A转盘被分成如图所示的三份(一个半圆,两个四分之一圆),并分别标有数字1,2,﹣3;B转盘被等分成三份,分别标有数字﹣1,﹣2,3.
16.(1)、化简:(2)、解不等式组17. 由于疫情爆发,张明一家小区被管控,规定每两日每户可派一人出小区购买生活必需品.为增添生活乐趣,张明制作了下面两个可以自由转动的转盘:A转盘被分成如图所示的三份(一个半圆,两个四分之一圆),并分别标有数字1,2,﹣3;B转盘被等分成三份,分别标有数字﹣1,﹣2,3. (1)、A转盘转出-3的概率是.(2)、张明让爸妈两人同时转动A、B两个转盘,规则如下:当转盘停止转动时(两个指针只要有一个指针停在分割线上时,重新转动两个转盘,直到指针停在标有数字的扇形区域),如果指针所指的数字之和为正数,则爸爸去;如果指针所指的数字之和为负数,则妈妈去.请问,这个游戏对双方公平吗?说明理由.18. 安徽滁州琅琊山会峰阁更名为琅琊阁,如图①是悬挂着巨大匾额的琅琊阁,如图②,线段 是悬挂在墙壁 上的匾额的截面示意图,已知 米, ,从水平地面点 处看点 ,仰角 ,从点 处看点 ,仰角 .且 米,求匾额悬挂的高度 的长.(结果精确到0.1米,参考数据: , , ).
(1)、A转盘转出-3的概率是.(2)、张明让爸妈两人同时转动A、B两个转盘,规则如下:当转盘停止转动时(两个指针只要有一个指针停在分割线上时,重新转动两个转盘,直到指针停在标有数字的扇形区域),如果指针所指的数字之和为正数,则爸爸去;如果指针所指的数字之和为负数,则妈妈去.请问,这个游戏对双方公平吗?说明理由.18. 安徽滁州琅琊山会峰阁更名为琅琊阁,如图①是悬挂着巨大匾额的琅琊阁,如图②,线段 是悬挂在墙壁 上的匾额的截面示意图,已知 米, ,从水平地面点 处看点 ,仰角 ,从点 处看点 ,仰角 .且 米,求匾额悬挂的高度 的长.(结果精确到0.1米,参考数据: , , ). 19. 本月初我市市区某校九年级学生进行一次体育模拟测试,并将目标效果测试中第二类选考项目(足球运球、篮球运球、排球垫球任选一项)的情况进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:
19. 本月初我市市区某校九年级学生进行一次体育模拟测试,并将目标效果测试中第二类选考项目(足球运球、篮球运球、排球垫球任选一项)的情况进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题: (1)、学校参加本次测试和参加“排球垫球”测试的人数分别是多少人?(2)、“篮球运球”的中位数落在等级;(3)、将本次测试“足球运球”、“篮球运球”、“排球垫球”三项等级折算成分数,则它们的平均成绩分别为6.5分,7.6分,8分,求参加本次测试的学生第二类选考项目的平均成绩;(4)、青岛市今年参加体育中考的人数约为8.5万人,你能否估计今年全市选择“篮球运球”的考生会有多少人?若能,求出其人数;若不能,请说明理由.20. 如图,已知ABCD,EF为BC边上的垂直平分线, , 且 .
(1)、学校参加本次测试和参加“排球垫球”测试的人数分别是多少人?(2)、“篮球运球”的中位数落在等级;(3)、将本次测试“足球运球”、“篮球运球”、“排球垫球”三项等级折算成分数,则它们的平均成绩分别为6.5分,7.6分,8分,求参加本次测试的学生第二类选考项目的平均成绩;(4)、青岛市今年参加体育中考的人数约为8.5万人,你能否估计今年全市选择“篮球运球”的考生会有多少人?若能,求出其人数;若不能,请说明理由.20. 如图,已知ABCD,EF为BC边上的垂直平分线, , 且 . (1)、求证:;(2)、连接AF,请判断四边形ABDF的形状,并说明理由.21. 长为的春游队伍,以的速度向东行进,如图1和图2,当队伍排尾行进到位置O时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为 , 当甲返回排尾后,他及队伍均停止行进.设排尾从位置O开始行进的时间为 , 排头与O的距离为
(1)、求证:;(2)、连接AF,请判断四边形ABDF的形状,并说明理由.21. 长为的春游队伍,以的速度向东行进,如图1和图2,当队伍排尾行进到位置O时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为 , 当甲返回排尾后,他及队伍均停止行进.设排尾从位置O开始行进的时间为 , 排头与O的距离为 (1)、当时,解答:
(1)、当时,解答:①求与t的函数关系式(不写t的取值范围);
②当甲赶到排头位置时,求的值;在甲从排头返回到排尾过程中,设甲与位置O的距离为 , 求与t的函数关系式(不写t的取值范围)
(2)、设甲这次往返队伍的总时间为 , 求T与v的函数关系式(不写v的取值范围),并写出队伍在此过程中行进的路程.22. 综合与实践 (1)、知识再现
(1)、知识再现
如图 , 中, , 分别以、、为边向外作的正方形的面积为、、 . 当 , 时, .(2)、问题探究如图,中, .
如图 , 分别以、、为边向外作的等腰直角三角形的面积为、、 , 则、、之间的数量关系是 .(3)、如图 , 分别以、、为边向外作的等边三角形的面积为、、 , 试猜想、、之间的数量关系,并说明理由.(4)、实践应用
如图4,将图中的绕点逆时针旋转一定角度至 , 绕点顺时针旋转一定角度至 , 、相交于点 . 求证:;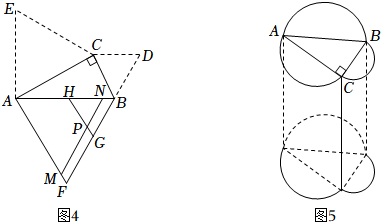 (5)、如图5,分别以图中的边、、为直径向外作半圆,再以所得图形为底面作柱体,、、为直径的半圆柱的体积分别为、、 . 若 , 柱体的高 , 直接写出的值.23. 第二十四届冬奥会在北京成功举办,我国选手在跳台滑雪项目中夺得金牌.在该项目中,首先沿着跳台助滑道飞速下滑,然后在起跳点腾空,身体在空中飞行至着陆坡着陆,再滑行到停止区终止本项目.主要考核运动员的飞行距离和动作姿态,某数学兴趣小组对该项目中的数学问题进行了深入研究:
(5)、如图5,分别以图中的边、、为直径向外作半圆,再以所得图形为底面作柱体,、、为直径的半圆柱的体积分别为、、 . 若 , 柱体的高 , 直接写出的值.23. 第二十四届冬奥会在北京成功举办,我国选手在跳台滑雪项目中夺得金牌.在该项目中,首先沿着跳台助滑道飞速下滑,然后在起跳点腾空,身体在空中飞行至着陆坡着陆,再滑行到停止区终止本项目.主要考核运动员的飞行距离和动作姿态,某数学兴趣小组对该项目中的数学问题进行了深入研究:下图为该兴趣小组绘制的赛道截面图,以停止区CD所在水平线为x轴,过起跳点A与x轴垂直的直线为y轴,O为坐标原点,建立平面直角坐标系.着陆坡AC的坡角为30°, . 某运动员在A处起跳腾空后,飞行至着陆坡的B处着陆, . 在空中飞行过程中,运动员到x轴的距离与水平方向移动的距离具备二次函数关系,其解析式为 .
 (1)、求b、c的值;(2)、进一步研究发现运动员在飞行过程中,其水平方向移动的距离与飞行时间具备一次函数关系,当运动员在起跳点腾空时, , ;空中飞行5s后着陆.
(1)、求b、c的值;(2)、进一步研究发现运动员在飞行过程中,其水平方向移动的距离与飞行时间具备一次函数关系,当运动员在起跳点腾空时, , ;空中飞行5s后着陆.①求x关于t的函数解析式;
②当t为何值时,运动员离着陆坡的竖直距离h最大,最大值是多少?
24. 如图1,在等边中, , 动点P从点A出发以的速度沿匀速运动,动点Q同时从点C出发以同样的速度沿的延长线方向匀速运动,当点P到达点B时,点P、Q同时停止运动.设运动时间为 , 过点P作于E,交边于D,线段的中点为M,连接 . (1)、当时,求t的值;(2)、在点P、Q运动过程中,点D、E也随之运动,线段的长度是否会发生变化?若发生变化,请说明理由,若不发生变化,求的长;(3)、连接 , 设四边形的面积为S,求S与t之间的函数关系式;(4)、如图2,将沿直线翻折,得 , 连接 , 当t为何值时,的值最小?并求出最小值.
(1)、当时,求t的值;(2)、在点P、Q运动过程中,点D、E也随之运动,线段的长度是否会发生变化?若发生变化,请说明理由,若不发生变化,求的长;(3)、连接 , 设四边形的面积为S,求S与t之间的函数关系式;(4)、如图2,将沿直线翻折,得 , 连接 , 当t为何值时,的值最小?并求出最小值.