山东省济南市历下区片区2023年联考模拟测试数学试卷(二)
试卷更新日期:2023-03-17 类型:中考模拟
一、单选题
-
1. -2的绝对值是( )A、2 B、 C、 D、2. 2022年十三届全国人大五次会议审议通过的政府工作报告中提出,今年城镇新增就业目标为11000000人以上.数据11000000用科学记数法表示应为( )A、 B、 C、 D、3. 如图所示三棱柱的主视图是( )
 A、
A、 B、
B、 C、
C、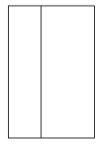 D、
D、 4. 如图,平行线 , 被直线所截,平分 , 若 , 则的度数是( )
4. 如图,平行线 , 被直线所截,平分 , 若 , 则的度数是( )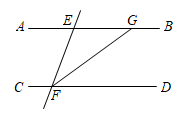 A、 B、 C、 D、5. 北京冬奥会和冬残奥会组委会收到来自全球的会徽设计方案共4506件,其中很多设计方案体现了对称之美.以下4幅设计方案中,既是轴对称图形又是中心对称图形的是( )A、
A、 B、 C、 D、5. 北京冬奥会和冬残奥会组委会收到来自全球的会徽设计方案共4506件,其中很多设计方案体现了对称之美.以下4幅设计方案中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 化简的结果是( )A、 B、 C、 D、7. 根据图像,可得关于x的不等式的解集是( )
6. 化简的结果是( )A、 B、 C、 D、7. 根据图像,可得关于x的不等式的解集是( )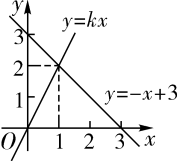 A、 B、 C、 D、8. 一次函数 与反比例函数 在同一坐标系中的大致图象是( )A、
A、 B、 C、 D、8. 一次函数 与反比例函数 在同一坐标系中的大致图象是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于 BD长为半径画弧,两弧相交于点M,作射线CM交AB于点E.若AE=2,BE=1,则EC的长度是( )
9. 如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于 BD长为半径画弧,两弧相交于点M,作射线CM交AB于点E.若AE=2,BE=1,则EC的长度是( )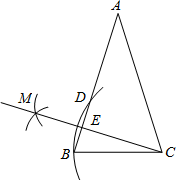 A、2 B、3 C、 D、10. 定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形 中,点 ,点 ,则互异二次函数 与正方形 有交点时 的最大值和最小值分别是( )
A、2 B、3 C、 D、10. 定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形 中,点 ,点 ,则互异二次函数 与正方形 有交点时 的最大值和最小值分别是( ) A、4,-1 B、 ,-1 C、4,0 D、 ,-1
A、4,-1 B、 ,-1 C、4,0 D、 ,-1二、填空题
-
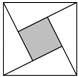
11. 因式分解:x2﹣4y2=.12. 分式方程 的解是 .13. “赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).小亮随机地向大正方形内部区域投飞镖.若直角三角形两条直角边的长分别是2和1,则飞镖投到小正方形(阴影)区域的概率是 .
 14. 如图,以正方形ABCD的AB边向外作正六边形ABEFGH,连接DH,则∠ADH=°
14. 如图,以正方形ABCD的AB边向外作正六边形ABEFGH,连接DH,则∠ADH=°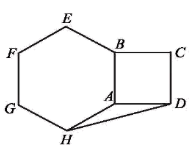 15. A,B两地相距240 km,甲货车从A地以40km/h的速度匀速前往B地,到达B地后停止,在甲出发的同时,乙货车从B地沿同一公路匀速前往A地,到达A地后停止,两车之间的路程y(km)与甲货车出发时间x(h)之间的函数关系如图中的折线 所示.其中点C的坐标是 ,点D的坐标是 ,则点E的坐标是 .
15. A,B两地相距240 km,甲货车从A地以40km/h的速度匀速前往B地,到达B地后停止,在甲出发的同时,乙货车从B地沿同一公路匀速前往A地,到达A地后停止,两车之间的路程y(km)与甲货车出发时间x(h)之间的函数关系如图中的折线 所示.其中点C的坐标是 ,点D的坐标是 ,则点E的坐标是 . 16. 如图,在菱形中, , 点E在边上,将沿直线翻折 , 得到 , 点B的对应点是点 . 若 , , 则的长是 .
16. 如图,在菱形中, , 点E在边上,将沿直线翻折 , 得到 , 点B的对应点是点 . 若 , , 则的长是 .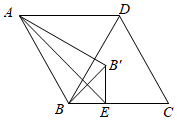
三、解答题
-
17. 计算:18. 解不等式组: , 并写出它的正整数解.19. 如图,矩形ABCD中,点M在DC上,AM=AB,且BN⊥AM,垂足为N,证明:△ABN≌△MAD;
 20. 为宣传6月8日世界海洋日,某校九年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩进行整理、描述和分析,其中部分学生的成绩在这一组的数据为:80,89,88,81,82,87,85,83,83,87,88,86,84,83,并绘制了如下不完整的统计表和统计图(如图).
20. 为宣传6月8日世界海洋日,某校九年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩进行整理、描述和分析,其中部分学生的成绩在这一组的数据为:80,89,88,81,82,87,85,83,83,87,88,86,84,83,并绘制了如下不完整的统计表和统计图(如图).知识竞赛成绩分组统计表
组别
分数/分
频数
A
a
B
10
C
14
D
18

请根据图表信息解答以下问题:
(1)、本次调查一共随机抽取了个参赛学生的成绩;(2)、表1中a=;(3)、所抽取的参赛学生的成绩的中位数是分;(4)、请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生约有多少人?21. 如图,为的直径,直线l与相切于点C, , 垂足为D,交于点E,连接 . (1)、求证:平分;(2)、若 , , 求的半径.22. 年月日是我国第个“全国消防宣传日”,该年“消防宣传月”活动的主题是“落实消防责任,防范安全风险”.为落实该主题,济南市消防大队到建东小区进行消防演习.已知,图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂可伸缩(),且起重臂可绕点A在一定范围内转动,张角为(),转动点A距离地面的高度为 .
(1)、求证:平分;(2)、若 , , 求的半径.22. 年月日是我国第个“全国消防宣传日”,该年“消防宣传月”活动的主题是“落实消防责任,防范安全风险”.为落实该主题,济南市消防大队到建东小区进行消防演习.已知,图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂可伸缩(),且起重臂可绕点A在一定范围内转动,张角为(),转动点A距离地面的高度为 . (1)、当起重臂长度为 , 张角 , 求云梯消防车最高点C距离地面
(1)、当起重臂长度为 , 张角 , 求云梯消防车最高点C距离地面的高度;
(2)、已知该小区层高为 , 若某居民家突发险情,请问该消防车有效救援能达到几层?请说明理由.(结果精确到 , 参考数据: , , , )23. 为响应传统文化进校园的号召,某校决定从网店购买《论语》和《弟子规》两种图书以供学生课外阅读.已知两种图书的购买信息如下表:《论语》数量/本
《弟子规》数量/本
总费用(元)
40
30
1250
50
20
1300
(1)、《论语》和《弟子规》每本的价格分别是多少元?(2)、若学校计划购买《论语》和《弟子规》两种图书共100本,《弟子规》的数量不超过《论语》数量的2倍.请设计出最省钱的购买方案,并求出此方案的总费用.24. 反比例函数在第一象限内的图象与的边交于点 , 与斜边交于点 , 已知点A坐标 , . (1)、求m,n以及反比例函数的解析式;(2)、求的面积;(3)、设P是线段边上的点,是否存在点P,以B,C,P为顶点的三角形与相似?若存在,求出此时点P的坐标;若不存在,请说明理由.25.
(1)、求m,n以及反比例函数的解析式;(2)、求的面积;(3)、设P是线段边上的点,是否存在点P,以B,C,P为顶点的三角形与相似?若存在,求出此时点P的坐标;若不存在,请说明理由.25. (1)、【问题呈现】如图1,和都是等边三角形,连接 , . 请判断与的数量关系: .(2)、【类比探究】如图2,和都是等腰直角三角形, . 连接 , . 请写出与的数量关系: .(3)、【拓展提升】如图3,和都是直角三角形, , 且 . 连接 , .
(1)、【问题呈现】如图1,和都是等边三角形,连接 , . 请判断与的数量关系: .(2)、【类比探究】如图2,和都是等腰直角三角形, . 连接 , . 请写出与的数量关系: .(3)、【拓展提升】如图3,和都是直角三角形, , 且 . 连接 , .①求的值;
②延长交于点F,交于点G.求的值.
26. 如图1,抛物线与x轴交于点A、(A点在B点左侧),与y轴交于点 , 点P是抛物线上一个动点,连接 (1)、求抛物线的函数表达式;(2)、如图2所示,当点P在直线上方运动时,连接 , 求四边形面积的最大值,并写出此时P点坐标.(3)、若点M是x轴上的一个动点,点N是抛物线上一动点,P的横坐标为 . 试判断是否存在这样的点M,使得以点为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
(1)、求抛物线的函数表达式;(2)、如图2所示,当点P在直线上方运动时,连接 , 求四边形面积的最大值,并写出此时P点坐标.(3)、若点M是x轴上的一个动点,点N是抛物线上一动点,P的横坐标为 . 试判断是否存在这样的点M,使得以点为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.