山东省济南市历下区2023年九校联合九年级学业水平模拟考试数学试题
试卷更新日期:2023-03-17 类型:中考模拟
一、单选题
-
1. -7的倒数是( )A、 B、 C、 D、72. 某地区计划到2025年建成6470万亩高标准农田,其中6470万用科学记数法表示为( )A、 B、 C、 D、3. 下列图形既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 如图, , 分别与 , 交于点 , , ,则 的度数为( )
4. 下列计算正确的是( )A、 B、 C、 D、5. 如图, , 分别与 , 交于点 , , ,则 的度数为( )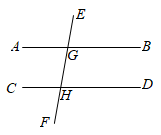 A、 B、 C、 D、6. “杂交水稻之父”袁隆平培育的超级杂交稻在全世界推广种植.某种植户为了考察所种植的杂交水稻苗的长势,从稻田中随机抽取9株水稻苗,测得苗高(单位:cm)分别是:22,23,24,23,24,25,26,23,25.则这组数据的众数和中位数分别是( )A、24,25 B、23,23 C、23,24 D、24,247. 如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )
A、 B、 C、 D、6. “杂交水稻之父”袁隆平培育的超级杂交稻在全世界推广种植.某种植户为了考察所种植的杂交水稻苗的长势,从稻田中随机抽取9株水稻苗,测得苗高(单位:cm)分别是:22,23,24,23,24,25,26,23,25.则这组数据的众数和中位数分别是( )A、24,25 B、23,23 C、23,24 D、24,247. 如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )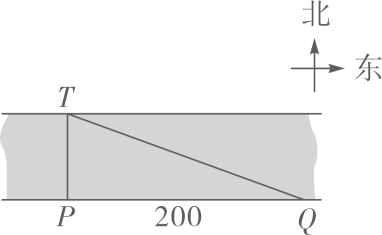 A、200tan70°米 B、 米 C、200sin70°米 D、 米8. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、9. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返同,且往返速度的大小不变,两车离甲地的距离 (单位: )与慢车行驶时间 (单位: )的函数关系如图,则两车先后两次相遇的间隔时间是( )
A、200tan70°米 B、 米 C、200sin70°米 D、 米8. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、9. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返同,且往返速度的大小不变,两车离甲地的距离 (单位: )与慢车行驶时间 (单位: )的函数关系如图,则两车先后两次相遇的间隔时间是( )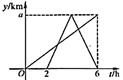 A、 B、 C、 D、10. 如图,正方形ABCD的对角线AC,BD相交于点O,点F是CD上一点,交BC于点E,连接AE,BF交于点P,连接OP.则下列结论:①;②;③;④若 , 则;⑤四边形OECF的面积是正方形ABCD面积的 . 其中正确的结论是( )
A、 B、 C、 D、10. 如图,正方形ABCD的对角线AC,BD相交于点O,点F是CD上一点,交BC于点E,连接AE,BF交于点P,连接OP.则下列结论:①;②;③;④若 , 则;⑤四边形OECF的面积是正方形ABCD面积的 . 其中正确的结论是( ) A、①②④⑤ B、①②③⑤ C、①②③④ D、①③④⑤
A、①②④⑤ B、①②③⑤ C、①②③④ D、①③④⑤二、填空题
-
11. 分解因式: .12. 方程 的解为 .13. 已知 , 是一元二次方程 的两根,则 .14. 如图,在平面直角坐标系中,ABCO为平行四边形,O(0,0),A(3,1),B(1,2),反比例函数 的图象经过▱OABC的顶点C,则k= .
 15. 如图,将 沿对角线 翻折,点 落在点 处, 交 于点 ,若 , , , ,则 的周长为 .
15. 如图,将 沿对角线 翻折,点 落在点 处, 交 于点 ,若 , , , ,则 的周长为 .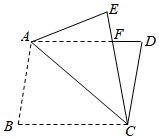 16. 如图(1),在 中, , ,边 上的点 从顶点 出发,向顶点 运动,同时,边 上的点 从顶点 出发,向顶点 运动, , 两点运动速度的大小相等,设 , , 关于 的函数图象如图(2),图象过点 ,则图象最低点的横坐标是.
16. 如图(1),在 中, , ,边 上的点 从顶点 出发,向顶点 运动,同时,边 上的点 从顶点 出发,向顶点 运动, , 两点运动速度的大小相等,设 , , 关于 的函数图象如图(2),图象过点 ,则图象最低点的横坐标是.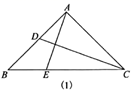

三、解答题
-
17. 计算: .18. 解不等式组19. 如图, , , 直线与 , 的延长线分别交于点E,F,求证: .
 20. 为有效推进儿童青少年近视防控工作,某学校决定开设以下四种球类的户外体育选修课程:篮球、足球、排球、乒乓球.为了解学生需求,该校随机对本校部分学生进行了“你选择哪种球类课程”的调查(要求必须选择且只能选择其中一门课程),并根据调查结果绘制成不完整的统计图表.
20. 为有效推进儿童青少年近视防控工作,某学校决定开设以下四种球类的户外体育选修课程:篮球、足球、排球、乒乓球.为了解学生需求,该校随机对本校部分学生进行了“你选择哪种球类课程”的调查(要求必须选择且只能选择其中一门课程),并根据调查结果绘制成不完整的统计图表.课程
人数
篮球
m
足球
21
排球
30
乒乓球
n

根据图表信息,解答下列问题:
(1)、分别求出表中m,n的值;(2)、求扇形统计图中“足球”对应的扇形圆心角的度数;(3)、该校共有2000名学生,请你估计其中选择“乒乓球”课程的学生人数.21. 如图,AB为⊙O的直径,点C在⊙O上,AD与过点C的切线互相垂直,垂足为D.连接BC并延长,交AD的延长线于点E. (1)、求证:AE=AB;(2)、若AB=10,BC=6,求CD的长.22. 端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元,某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同.在销售中,该商家发现猪肉粽每盒售价50元时,每天可售出100盒;每盒售价提高1元时,每天少售出2盒.(1)、求猪肉粽和豆沙粽每盒的进价;(2)、设猪肉粽每盒售价x元 表示该商家每天销售猪肉粽的利润(单位:元),求y关于x的函数解析式并求最大利润.23. 在直角坐标系中,设函数 是常数, 与函数 ( 是常数, 的图象交于点 ,点 关于 轴的对称点为点 .
(1)、求证:AE=AB;(2)、若AB=10,BC=6,求CD的长.22. 端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元,某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同.在销售中,该商家发现猪肉粽每盒售价50元时,每天可售出100盒;每盒售价提高1元时,每天少售出2盒.(1)、求猪肉粽和豆沙粽每盒的进价;(2)、设猪肉粽每盒售价x元 表示该商家每天销售猪肉粽的利润(单位:元),求y关于x的函数解析式并求最大利润.23. 在直角坐标系中,设函数 是常数, 与函数 ( 是常数, 的图象交于点 ,点 关于 轴的对称点为点 . (1)、若点 的坐标为 ,
(1)、若点 的坐标为 ,①求 的值;
②当 时,直接写出 的取值范围.
(2)、若点 在函数 是常数, 的图象上,求 的值.24. 对于任意一个四位数m,若千位上的数字与个位上的数字之和是百位上的数字与十位上的数字之和的2倍,则称这个四位数m为“共生数”.例如: , 因为 , 所以是“共生数”; , 因为 , 所以不是“共生数”.(1)、判断5313,6437是否为“共生数”?并说明理由:(2)、对于“共生数”n,当十位上的数字是千位上的数字的2倍,百位上的数字与个位上的数字之和能被9整除时,记 . 求满足是偶数的所有共生数.25. 如图1,在矩形ABCD中, , .点E是线段AD上的动点(点E不与点A,D重合),连接CE,过点E作 ,交AB于点F. (1)、求证: ;(2)、如图2,连接CF,过点B作 ,垂足为G,连接AG.点M是线段BC的中点,连接GM.
(1)、求证: ;(2)、如图2,连接CF,过点B作 ,垂足为G,连接AG.点M是线段BC的中点,连接GM.①求 的最小值;
②当 取最小值时,求线段DE的长.
26. 如图,在平面直角坐标系中,抛物线与x轴交于点与y轴交于点C. (1)、求该抛物线的解析式:(2)、直线l为该抛物线的对称轴,点D与点C关于直线l对称,点F为直线下方抛物线上一动点,连接 , 求面积的最大值:(3)、在(2)的条件下,将抛物线沿射线平移4个单位,得到新的抛物线 , 点E为点F的对应点,点P为的对称轴上任意一点,在上确定一点Q,使得以点D,E,P,Q为顶点的四边形是平行四边形,请直接写出所有符合条件的点Q的坐标.
(1)、求该抛物线的解析式:(2)、直线l为该抛物线的对称轴,点D与点C关于直线l对称,点F为直线下方抛物线上一动点,连接 , 求面积的最大值:(3)、在(2)的条件下,将抛物线沿射线平移4个单位,得到新的抛物线 , 点E为点F的对应点,点P为的对称轴上任意一点,在上确定一点Q,使得以点D,E,P,Q为顶点的四边形是平行四边形,请直接写出所有符合条件的点Q的坐标.