山东省济南市莱芜区2023年数学中考第一次模拟试题

试卷更新日期：2023-03-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 4的算术平方根是（）

A、2 B、±2 C、16 D、±16

查看试题解析
2. 下列几何体中，俯视图与主视图完全相同的几何体是（）

A、圆锥 B、球 C、圆柱 D、长方体

查看试题解析
3. 根据世界卫生组织的统计，截止2022年1月16日，全球新冠确诊病例累计超过32620万，用科学记数法表示这一数据是（）

A、 $3.262 \times 1 0^{8}$ B、 $0.3262 \times 1 0^{9}$ C、 $32.62 \times 1 0^{7}$ D、 $3.262 \times 1 0^{9}$

查看试题解析
4. 如图，在 $△ D E F$ 中，点C在 $D F$ 的延长线上，点B在 $E F$ 上，且 $A B ∥ C D$ ， $∠ E B A = 80 °$ ，则 $∠ E + ∠ D$ 的度数为（）

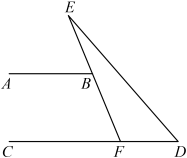A、60° B、30° C、90° D、80°

查看试题解析
5. 下列图案是我国几家银行的标志，其中既是轴对称图形又是中心对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 下列说法：① $\sqrt{2} - 1$ 的相反数是 $- \sqrt{2} - 1$ ；②算术平方根等于它本身的数只有零；③数轴上的点不是表示有理数，就是表示无理数；④若 $a$ ， $b$ 都是无理数，则 $| a | + | b |$ 一定是无理数．其中正确的有（）．

A、4个 B、3个 C、2个 D、1个

查看试题解析
7. 化简 $\frac{a^{2}}{a － b}$ － $\frac{b^{2}}{a － b}$ 的结果是（）．

A、a－b B、a+b C、 $\frac{a + b}{a － b}$ D、 $\frac{a － b}{a + b}$

查看试题解析
8. 初三(1)班周沫同学拿了A，B，C，D四把钥匙去开教师前、后门的锁，其中A钥匙只能开前门，B钥匙只能开后门，任意取出一把钥匙能够一次打开教室门的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{3}{4}$ C、1 D、 $\frac{1}{4}$

查看试题解析
9. 如图，在平面直角坐标系中， $Δ A B C$ 的顶点都在格点上，如果将 $Δ A B C$ 沿 $y$ 轴翻折，得到△ $A^{'} B^{'} C^{'}$ ，那么点 $B$ 的对应点 $B^{'}$ 的坐标为（）

A、 $(0 ， 2)$ B、 $(3 ， 1)$ C、 $(1 ， 4)$ D、 $(- 3 ， - 1)$

查看试题解析
10. 如图，矩形 $A B C D$ 的一边 $C D$ 在x轴上，顶点A、B分别落在双曲线 $y = \frac{1}{x}$ 、 $y = \frac{4}{x}$ 上，边 $B C$ 交 $y = \frac{1}{x}$ 于点E，连接 $A E$ ，则 $△ A B E$ 的面积为（）

A、 $\frac{9}{4}$ B、 $\frac{3}{4}$ C、 $\frac{3}{8}$ D、 $\frac{9}{8}$

查看试题解析
11. 已知 $A (m, 2020)$ ， $B (m + n, 2020)$ 是抛物线 $y = - {(x - h)}^{2} + 2036$ 上两点，则正数 $n =$ （）

A、2 B、4 C、8 D、16

查看试题解析
12. 如图，在矩形纸片 $A B C D$ 中，将 $A B$ 沿 $B M$ 翻折，使点A落在 $B C$ 上的点N处， $B M$ 为折痕，连接 $M N$ ；再将 $C D$ 沿 $C E$ 翻折，使点D恰好落在 $M N$ 上的点F处， $C E$ 为折痕，连接 $E F$ 并延长交 $B M$ 于点P，若 $A D = 24 ， A B = 15$ ，则线段 $P E$ 的长等于（）

A、22 B、20 C、18 D、16

查看试题解析

二、填空题

13. 因式分解： $x^{2} + 2 x + 1 =$ .

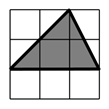
查看试题解析
14. 如图，小明向图中的格盘中随意投掷一枚棋子，该棋子落在三角形内的概率是；

查看试题解析
15. 已知正多边形的一个外角等于60°，则这个正多边形的内角和的度数为.

查看试题解析
16. 已知关于x的一元二次方程 $x^{2} + k x - 6 = 0$ 的一个根是2，则另一个根的值是．

查看试题解析
17. 一列慢车从 $A$ 地驶往 $B$ 地，一列快车从 $B$ 地驶往 $A$ 地.两车同时出发，各自抵达目的地后停止，如图所示，折线表示两车之间的距离 $y$ （km）与慢车行驶时间 $t$ （h）之间的关系.当快车到达 $A$ 地时，慢车与 $B$ 地的距离为km.

查看试题解析
18. 如图，在正方形ABCD中，点E是边CD上一点，BF⊥AE，垂足为F，将正方形沿AE.BF切割分成三块，再将△ABF和△ADE分别平移，拼成矩形BGHF.若BG=kBF，则 $\frac{D E}{D C} =$ (用含k的式子表示)

查看试题解析

三、解答题

19.

(1)、计算： $(\frac{π}{2})^{0} - 2 s i n 30 ° + \sqrt{4} + (\frac{1}{2})^{- 1}$ ；

(2)、解不等式组： ${\begin{array}{l} 4 (2 x - 1) \leq 3 x + 1 ① \\ 2 x > \frac{x - 3}{2} ② \end{array}$ ，并写出它的所有整数解．

查看试题解析
20. 为降低校园欺凌事件发生的频率，某课题组针对义务教育阶段学生校园欺凌事件发生状况进行调查并分析．课题组对全国可查的2800例欺凌事件发生原因进行抽样调查并分析，所得数据绘制成统计图如下：根据以上信息，回答下列问题：

(1)、本次抽样调查的样本容量为．

(2)、补全条形统计图；

(3)、在欺凌事件发生原因扇形统计图中，“因琐事”区域所在扇形的圆心角的度数为．

(4)、估计所有2800例欺凌事件中有多少事件是“因琐事”或因“发泄情绪”而导致事件发生的？

查看试题解析
21. 如图， $A B$ 是⊙O的直径，点C是⊙ $O$ 上一点， $A D$ 与过点C的切线垂直，垂足为点D，直线 $D C$ 与 $A B$ 的延长线相交于点P，弦 $C E$ 平分 $∠ A C B$ ，交 $A B$ 于点F，连接 $B E$ ．

(1)、求证： $A C$ 平分 $∠ D A B$ ；

(2)、若 $t a n ∠ A B C = \frac{4}{3}$ ， $B E = 5 \sqrt{2}$ ，求线段 $A D$ 的长．

查看试题解析
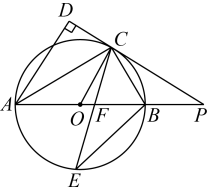22. 在一次综合实践活动中，数学兴趣小组的同学想要测量一楼房 $A B$ 的高度，如图，楼房 $A B$ 后有一假山，其斜坡 $C D$ 坡比为1∶ $\sqrt{3}$ ，山坡坡面上点E处有一休息亭，在此处测得楼顶A的仰角为 $45 °$ ，假山坡脚C与楼房水平距离 $B C = 30$ 米，与亭子距离 $C E = 40$ 米．

(1)、求点E距水平地面 $B C$ 的高度；

(2)、求楼房 $A B$ 的高．（结果精确到整数，参考数据 $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732$ ）

查看试题解析
23. 为有效落实双减工作，切实做到减负提质，很多学校决定在课后看护中增加乒乓球项目．体育用品商店得知后，第一次用900元购进乒乓球若干盒，第二次又用900元购进该款乒乓球，但这次每盒的进价是第一次进价的 $1.2$ 倍，购进数量比第一次少了30盒．

(1)、求第一次每盒乒乓球的进价是多少元？

(2)、若要求这两次购进的乒乓球按同一价格全部销售完后获利不低于510元，则每盒乒乓球的售价至少是多少元？

查看试题解析
24. 如图1，在 $R t △ A B C$ 中， $∠ B A C ＝ 90 ° ， A B ＝ A C$ ， D，E两点分别在 $A B ， A C$ 上，且 $D E ∥ B C$ ，将 $△ A D E$ 绕点A顺时针旋转，记旋转角为 $α$ ．

(1)、问题发现当 $α ＝ 0 °$ 时，线段 $B D ， C E$ 的数量关系是；

(2)、拓展探究当 $0 ° \leq α ＜ 360 °$ 时，（1）中的结论有无变化？请仅就图2的情形给出证明；

(3)、问题解决设 $D E ＝ 2 ， B C ＝ 6 ， 0 ° \leq α ＜ 360 °$ ， $△ A D E$ 旋转至A，B，E三点共线时，直接写出线段 $B E$ 的长．

查看试题解析
25. 如图1所示，在平面直角坐标系中，抛物线 $y = a x^{2} + b x + c$ 经过 $A (- 3 ， 0)$ 、 $B (1 ， 0)$ 、 $C (0 ， 3)$ 三点．

(1)、求抛物线的函数解析式

(2)、如图2，点D为抛物线的顶点，连接AD，点P是线段AD上一个动点（不与A、D重合），过点P作y轴的垂线，垂足点为E，连接AE．如果P点的坐标为 $(x ， y)$ ， $△ P A E$ 的面积为S，求S与x之间的函数关系式（不用写出自变量x的取值范围）；

(3)、在（2）的条件下，当S取到最大值时，过点P作x轴的垂线，垂足为F，连接EF，把 $△ P E F$ 沿直线EF折叠，点P的对应点为点 $P^{'}$ ，求出 $P^{'}$ 的坐标．

查看试题解析