山东省济南市高新区2023年中考一模数学试题

试卷更新日期：2023-03-17 类型：中考模拟

进入出卷网下载

一、单选题

1. -2的绝对值是（）

A、2 B、 $\frac{1}{2}$ C、 $- \frac{1}{2}$ D、 $- 2$

查看试题解析
2. 如图所示的几何体的主视图是（　　）

A、 B、 C、 D、

查看试题解析
3. 神舟十四号载人飞船是北京时间2022年6月5日10时44分由长征二号F遥十四运载火箭成功送入近地点高度200000米、远地点350000米、倾角42°的地球近地轨道．将350000用科学记数法表示应为（　　）

A、 $3.5 \times 1 0^{4}$ B、 $0.35 \times 1 0^{5}$ C、 $35 \times 1 0^{4}$ D、 $3.5 \times 1 0^{5}$

查看试题解析
4. 将一副三角板(含30°、45°的直角三角形)摆放成如图所示，图中∠1的度数是（）

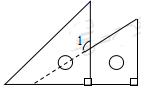A、90° B、120° C、135° D、150°

查看试题解析
5. 下列运算正确的是（）

A、 ${(x + 2)}^{2} = x^{2} + 4$ B、 $a^{2} + a^{2} = a^{4}$ C、 $2 x + 3 x = 5 x^{2}$ D、 ${(- 2 x^{3})}^{2} = 4 x^{6}$

查看试题解析
6. 10件产品中有5件次品，从中任意抽取1件，恰好抽到次品的概率是（　　）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{5}$

查看试题解析
7. 化简 $\frac{x}{x - 1} - \frac{1}{x + 1}$ 的结果是（）

A、1 B、 $x + 1$ C、 $x - 1$ D、 $\frac{x^{2} + 1}{x^{2} - 1}$

查看试题解析
8. A，B，C三种宽带上网方式的月收费金额 $y_{A}$ （元）， $y_{B}$ （元）， $y_{C}$ （元）与月上网时间x（小时）的对应关系如图所示．以下有四个推断中错误的是（　　）

A、月上网时间不足35小时，选择方式A最省钱； B、月上网时间超过55小时且不足80小时，选择方式C最省钱； C、对于上网方式B，若月上网时间在60小时以内，则月收费金额为60元； D、对于上网方式C，无论月上网时间是多久，月收费都是120元．

查看试题解析
9. 问题：如图 $1$ ，矩形纸片 $A B C D$ 中， $A B = 2$ ， $B C = 3$ ，要求将矩形纸片剪两刀后不重叠、无缝隙地拼接成一个正方形．甲、乙两位同学根据剪拼前后面积不变，确定了正方形的边长为 $\sqrt{6}$ ，并分别设计了如下的方案．
甲：如图 $2$ ，在 $A D$ 上找点E，连接 $B E$ ，使 $B E =$ $\sqrt{6}$ ，作 $∠ D C F = ∠ A E B$ ，交 $B E$ 于F点，完成分割；
乙：如图 $3$ ，在 $A D$ 上找点F，连接 $C F$ ，使 $C F =$ $\sqrt{6}$ ，以 $B C$ 为直径作圆，交 $C F$ 于点E，连接 $B E$ 即可完成分割．下列结论正确的是(　　)

A、甲、乙的分割都错误 B、甲、乙的分割都正确 C、乙的分割正确，图3中 $A F = \sqrt{2}$ D、甲的分割正确，图2中 $A E = 2 \sqrt{2}$

查看试题解析
10. 如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与 $x$ 轴交于点 $A (5 ， 0)$ ，与 $y$ 轴交于点 $C$ ，其对称轴为直线 $x = 2$ ，结合图象分析如下结论：① $a b c > 0$ ；② $b + 3 a < 0$ ；③当 $x > 0$ 时， $y$ 随 $x$ 的增大而增大；④点 $M$ 是抛物线的顶点，若 $C M ⊥ A M$ ，则 $a$ $= \frac{\sqrt{6}}{6}$ ．其中正确的有(　　)

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 因式分解： $9 - 4 x^{2} =$ ．

查看试题解析
12. 如图所示游戏板中每一个小正方形除颜色外都相同，把游戏板平放到露天地面上，落在该游戏板上的第一滴雨正好打中阴影部分的概率是.

查看试题解析
13. 已知实数 $a$ 在数轴上的位置如图所示，则化简 $| a - 1 | + \sqrt{a^{2}}$ 的结果是．

查看试题解析
14. 已知 $x^{2} - x = 2022$ ，则代数式 $(x + 1) (x - 1) + x (x - 2) =$ ．

查看试题解析
15. 某市的出租车收费标准如表：
里程/公里
收费/元
3公里以下（含3公里）
14
3公里以上，10公里以下（含10公里），每增加1公里
$2.4$
10公里以上，每增加1公里
$3.6$
当 $x > 10$ 时，收费y（元）与行驶里程x（公里）的函数关系式为．

查看试题解析
16. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 3$ ， $B C = \sqrt{3}$ ，把 $R t △ A B C$ 沿 $A B$ 翻折得到 $R t △ A B D$ ，过点B作 $B E ⊥ B C$ ，交 $A D$ 于点E，点F是线段 $B E$ 上一点，且 $t a n ∠ A D F = \frac{\sqrt{3}}{2}$ ．则下列结论中：① $A E = B E$ ；② $△ B E D ∽ △ A B C$ ；③ $B D^{2} = A D \cdot D E$ ；④ $A F = \frac{2 \sqrt{13}}{3}$ ．正确的有（把所有正确答案的序号都填上）

查看试题解析

三、解答题

17. 计算： $t a n 60 ° - | - \sqrt{3} | + {(\sqrt{5} - 1)}^{0} + {(\frac{1}{2})}^{- 2}$ ．

查看试题解析
18. 解不等式组： ${\begin{array}{l} 5 x - 3 < 4 x ① \\ \frac{x}{8} - \frac{1}{4} \leq \frac{x + 1}{2} ② \end{array}$ ，并把它的解集在数轴上表示出来．

查看试题解析
19. 如图，在▱ABCD中，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F．求证：△ABE≌△CDF．

查看试题解析
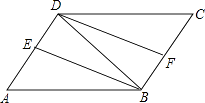20. 植树节期间，某校360名学生参加植树活动，要求每人植树3～6棵，活动结束后随机抽查了20名学生每人的植树量，并分为四种类型，A：3棵；B：4棵；C：5棵；D：6棵．根据各类型对应的人数绘制了扇形统计图（如图1）和尚未完成的条形统计图（如图2）．请解答下列问题：

(1)、将条形统计图补充完整；

(2)、这20名学生每人植树量的众数为棵，中位数为棵；

(3)、在求这20名学生每人植树量的平均数时，小宇是这样分析的：
第一步：求平均数的公式是 $\bar{x} = \frac{x_{1} + x_{2} + \dots + x_{n}}{n}$ ；
第二步：在该问题中，n=4， $x_{1} = 3$ ， $x_{2} = 4$ ， $x_{3} = 5$ ， $x_{4} = 6$ ；
第三步： $\bar{x} = \frac{3 + 4 + 5 + 6}{4} = 4.5 （棵）$ ．
①小宇的分析是错误的，他错在第几步？
请你帮他计算出正确的平均数，并估计这360名学生共植树多少棵．

查看试题解析
21. 为倡导“低碳生活”，人们常选择以自行车作为代步工具，如图是一辆自行车的部分几何示意图，其中车架档 $A C$ 与 $C D$ 的长分别为 $45 c m$ 和 $60 c m$ ，且它们互相垂直，座杆 $C E$ 的长为 $20 c m$ ，点A，C，E在同一条直线上，且 $∠ C A B = 75 °$ ．（参考数据： $s i n 75 ° \approx 0.966$ ， $c o s 75 ° \approx 0.259$ ， $t a n 75 ° \approx 3.732$ ）

(1)、求车架档 $A D$ 的长；

(2)、求车座点E到车架档 $A B$ 的距离（结果精确到 $1 c m$ ）．

查看试题解析
22. 如图， $A B$ 是 $⊙ O$ 的直径， $A E ⊥ E P$ ，垂足为E，直线 $E P$ 与圆相切于点C， $A E$ 交 $⊙ O$ 于点D，直线 $E C$ 交 $A B$ 的延长线于点P，连接 $A C$ ， $B C$ ．

(1)、求证： $A C$ 平分 $∠ B A D$ ；

(2)、若直径 $A B$ 为10， $B C = 6$ ，求 $D E$ 长．

查看试题解析
23. 在“新冠病毒”防控期间，某益康医疗器械公司分两次购进酒精消毒液与测温枪两种商品进行销售两次购进同一商品的进价相同，具体情况如表所示：
项目
购进数量（件）
购进所需费用（元）
酒精消毒液
测温枪
第一次
30
40
7560
第二次
40
30
5880

(1)、求酒精消毒液和测温枪两种商品每件的进价分别是多少元？

(2)、公司决定酒精消毒液以每件20元出售，测温枪以每件240元出售.为满足市场需求，需购进这两种商品共1000件，且酒精消毒液的数量不少于测温枪数量的4倍，求该公司销售完上述1000件商品获得的最大利润.

查看试题解析
24. 如图1，一次函数 $y = - 2 x + 4$ 的图象交x轴于点A，交y轴于点B，与反比例函数y $= \frac{k}{x}$ $(x > 0)$ 的图象交点 $C (1 ， n)$ ．

(1)、求反比例函数的解析式；

(2)、在双曲线 $y$ $= \frac{k}{x}$ $(x > 0)$ 上是否存在一点D，满足 $S_{△ O C D} = \frac{1}{2} S_{△ A O B}$ ，若存在，请求出点D坐标；若不存在，请说明理由．

(3)、如图2，过点B作 $B M ⊥ O B$ 交反比例函数 $y$ $= \frac{k}{x}$ $(x > 0)$ 的图象于点M，点N为反比例函数 $y$ $= \frac{k}{x}$ $(x > 0)$ 的图象上一点， $∠ A B M = ∠ B A N$ ，请直接写出点N的坐标．

查看试题解析
25. 如图，在 $△ A B C$ 中， $A B = A C$ ， E是线段BC上一动点（不与B、C重合），连接 $A E$ ，将线段 $A E$ 绕点A逆时针旋转与 $∠ B A C$ 相等的角度，得到线段 $A F$ ，连接 $E F$ ，点M和点N分别是边 $B C ， E F$ 的中点．

(1)、如图1，若 $∠ B A C = 120 °$ ，当点E是 $B C$ 边的中点时， $\frac{M N}{B E} =$ ，直线 $B E$ 与 $M N$ 相交所成的锐角的度数为度．

(2)、如图2，若 $∠ B A C = 120 °$ ，当点E是 $B C$ 边上任意一点时（不与 $B C$ 重合），上述两个结论是否成立？若成立，请写出证明过程；若不成立，请说明理由．

(3)、若 $∠ B A C = 60 ° ， A B = 6$ ，点E在直线 $B C$ 上运动， $\frac{B E}{C E} = \frac{1}{2}$ ，若其它条件不变，过点C作 $C P ∥ M N$ ，交直线 $E F$ 于P，直接写出P到 $B C$ 的距离．

查看试题解析
26. 如图，已知抛物线 $y = a x^{2} + b x + 4 (a \neq 0)$ 与x轴交于点A（1，0）和B，与y轴交于点C，对称轴为 $x = \frac{5}{2}$ .

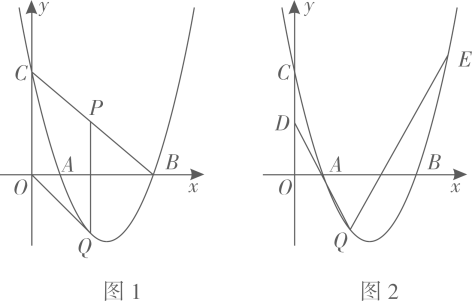(1)、求抛物线的解析式；

(2)、如图1，若点P是线段BC上的一个动点（不与点B，C重合），过点P作y轴的平行线交抛物线于点Q，连接OQ.当线段PQ长度最大时，判断四边形OCPQ的形状并说明理由.

(3)、如图2，在（2）的条件下，D是OC的中点，过点Q的直线与抛物线交于点E，且 $∠ D Q E = 2 ∠ O D Q$ .在y轴上是否存在点F，使得 $△ B E F$ 为等腰三角形？若存在，求点F的坐标；若不存在，请说明理由.

查看试题解析

里程/公里	收费/元
3公里以下（含3公里）	14
3公里以上，10公里以下（含10公里），每增加1公里	$2.4$
10公里以上，每增加1公里	$3.6$

项目	购进数量（件）		购进所需费用（元）
项目	酒精消毒液	测温枪	购进所需费用（元）
第一次	30	40	7560
第二次	40	30	5880