内蒙古自治区包头市2023年下学期九年级数学第一次模拟试题
试卷更新日期:2023-03-17 类型:中考模拟
一、单选题
-
1. 2022年冬奥运即将在北京举行,北京也即将成为迄今为止唯一个既举办过夏季奥运会,又举办过冬季奥运会的城市,据了解北京冬奥会的预算规模为15.6亿美元,政府补贴6%(9400万美元).其中1 560 000 000用科学记数法表示为( )A、 1.56×109 B、1.56×108 C、15.6×108 D、0.156×10102. 如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么 的值是
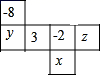 A、1 B、4 C、7 D、93. 函数 的自变量x的取值范围是( )A、 B、 C、 D、 且4. 在下列各事件中,可能性最大的是( )A、任意买一张电影票,座位号是奇数 B、掷一枚骰子点数小于等于 C、有张彩票,其中张是获奖彩票,从中抽一张就得奖 D、一个袋子中有个红球,个白球,从中摸出一个是白球5. 如图,BM是△ABC的角平分线,D是BC边上的一点,连接AD,使AD=DC,且∠BAD=120°,则∠AMB=( )
A、1 B、4 C、7 D、93. 函数 的自变量x的取值范围是( )A、 B、 C、 D、 且4. 在下列各事件中,可能性最大的是( )A、任意买一张电影票,座位号是奇数 B、掷一枚骰子点数小于等于 C、有张彩票,其中张是获奖彩票,从中抽一张就得奖 D、一个袋子中有个红球,个白球,从中摸出一个是白球5. 如图,BM是△ABC的角平分线,D是BC边上的一点,连接AD,使AD=DC,且∠BAD=120°,则∠AMB=( ) A、30° B、25° C、22.5° D、20°6. 已知下列命题:①若a>b,则a2>b2;②若a>1,则(a﹣1)0=1;③两个全等的三角形的面积相等;④四条边相等的四边形是菱形.其中原命题与逆命题均为真命题的个数是( )A、4个 B、3个 C、2个 D、1个7. 已知一组数据a,b,c的平均数为5,方差为4,那么数据a﹣2,b﹣2,c﹣2的平均数和方差分别是.( )A、3,2 B、3,4 C、5,2 D、5,48. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则图中阴影部分的面积是( )
A、30° B、25° C、22.5° D、20°6. 已知下列命题:①若a>b,则a2>b2;②若a>1,则(a﹣1)0=1;③两个全等的三角形的面积相等;④四条边相等的四边形是菱形.其中原命题与逆命题均为真命题的个数是( )A、4个 B、3个 C、2个 D、1个7. 已知一组数据a,b,c的平均数为5,方差为4,那么数据a﹣2,b﹣2,c﹣2的平均数和方差分别是.( )A、3,2 B、3,4 C、5,2 D、5,48. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则图中阴影部分的面积是( ) A、 B、 C、 - D、9. 若为方程的两个实数根,则的值为( )A、-13 B、12 C、14 D、1510. 某商店在节日期间开展优惠促销活动:购买原价超过200元的商品,超过200元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过200元的部分可以享受的优惠是( )
A、 B、 C、 - D、9. 若为方程的两个实数根,则的值为( )A、-13 B、12 C、14 D、1510. 某商店在节日期间开展优惠促销活动:购买原价超过200元的商品,超过200元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过200元的部分可以享受的优惠是( ) A、打八折 B、打七折 C、打六折 D、打五折11. 如图,直线与x轴、y轴交于A、B两点,的平分线所在的直线的解析式是( )
A、打八折 B、打七折 C、打六折 D、打五折11. 如图,直线与x轴、y轴交于A、B两点,的平分线所在的直线的解析式是( ) A、 B、 C、 D、12. 如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )
A、 B、 C、 D、12. 如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )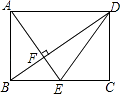 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 从 , 2, , 这四个数中任选两数,分别记作m,n,那么点在函数图象上的概率是 .14. 若关于x的不等式组有且只有两个整数解,则实数a的取值范围是 .15. 已知方程组 的解满足x+y=2,则k的值为16. 化简: , 结果为 .17. 如图,AB是⊙O的直径,AC、BC是⊙O的弦,直径DE⊥AC于点P.若点D在优弧ABC上,AB=8,BC=3,则DP= .
 18. 如图,在平行四边形ABCD中,E为边BC上一点,AC与DE相交于点F,若CE=2EB,S△AFD=9,则S△EFC等于 .
18. 如图,在平行四边形ABCD中,E为边BC上一点,AC与DE相交于点F,若CE=2EB,S△AFD=9,则S△EFC等于 .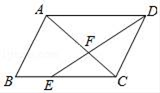 19. 如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y=的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为 .
19. 如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y=的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为 . 20. 如图,在矩形中, , E为边的中点,将绕点E顺时针旋转 , 点D对应点为C,点A的对应点为F,过点E作交BC于点M,交于点N,现有下列结论:
20. 如图,在矩形中, , E为边的中点,将绕点E顺时针旋转 , 点D对应点为C,点A的对应点为F,过点E作交BC于点M,交于点N,现有下列结论:①;②;③;④点N为的中点,其中正确的结论为 .

三、解答题
-
21. 2020年1月,国家发改委出台指导意见,要求2021年底前,所有城市原则上全面实行居民阶梯水价制度.小军为了解市政府调整水价方案的社会反响,随机访问了自己居住在小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1,图2.

小军发现每月每户的用水量在之间,有7户居民对用水价格调价涨幅抱无所谓,不用考虑用水方式的改变.根据小军绘制的图表和发现的信息,完成下列问题:
(1)、 , 小明调查了户居民,并补全图1 ;(2)、每月每户用水量的中位数落在之间,众数落在之间;(3)、如果小明所在的小区有1200户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?22. 阅读下面的材料,并回答所提出的问题:如图所示,在锐角三角形中,求证:这个三角形不是一个直角三角形,不能直接使用锐角三角函数的知识去处理,所以必须构造直角三角形,过点A作 , 垂足为D,则在和中由正弦定义可完成证明.
解:如图,过点A作 , 垂足为D,

在中, , 则
中, , 则
所以 , 即
(1)、在上述分析证明过程中,主要用到了下列三种数学思想方法的哪一种( )A、数形结合的思想; B、转化的思想; C、分类的思想(2)、用上述思想方法解答下面问题.在中, , 求和的面积.
(3)、用上述结论解答下面的问题(不必添加辅助线)在锐角三角形中, , 求的度数.
23. 某造纸厂为了保护环境,准备购买A,B两种型号的污水处理设备共6台,用于同时治理不同成分的污水,若购买A型2台,B型3台需54万元,购买A型4台、B型2台需68万元.(1)、求出A型、B型污水处理设备的单价;(2)、经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水180吨,如果该企业每月的污水处理量不低于1150吨,问共有几种购买方案?请你为该企业设计一种最省钱的购买方案并求此时的购买费用.24. 如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,圆O是△BEF的外接圆. (1)、求证:AC为圆O的切线;(2)、若tan∠CBE= , AE=4,求圆O的半径.25. 在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC,连接OB,点D为OB的中点,点E是线段AB上的动点,连接DE,作DF⊥DE,交OA于点F,连接EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.
(1)、求证:AC为圆O的切线;(2)、若tan∠CBE= , AE=4,求圆O的半径.25. 在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC,连接OB,点D为OB的中点,点E是线段AB上的动点,连接DE,作DF⊥DE,交OA于点F,连接EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒. (1)、如图1,当t=3时,求DF的长.(2)、如图2,当点E在线段AB上移动的过程中,的大小是否发生变化?如果变化,请说明理由;如果不变,请求出的值.(3)、连接AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.26. 如图,已知抛物线y=ax2+bx+c经过原点O(0,0)、A(2,0),直线y=2x经过抛物线的顶点B,点C是抛物线上一点,且位于对称轴的右侧,联结BC、OC、AB,过点C作CE∥x轴,分别交线段OB、AB于点E、F.
(1)、如图1,当t=3时,求DF的长.(2)、如图2,当点E在线段AB上移动的过程中,的大小是否发生变化?如果变化,请说明理由;如果不变,请求出的值.(3)、连接AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.26. 如图,已知抛物线y=ax2+bx+c经过原点O(0,0)、A(2,0),直线y=2x经过抛物线的顶点B,点C是抛物线上一点,且位于对称轴的右侧,联结BC、OC、AB,过点C作CE∥x轴,分别交线段OB、AB于点E、F. (1)、求抛物线的表达式;(2)、当BC=CE时,求证:△BCE∽△ABO;(3)、当∠CBA=∠BOC时,求点C的坐标.
(1)、求抛物线的表达式;(2)、当BC=CE时,求证:△BCE∽△ABO;(3)、当∠CBA=∠BOC时,求点C的坐标.