辽宁省鞍山市立山区2023年九年级中考一模数学试题
试卷更新日期:2023-03-17 类型:中考模拟
一、单选题
-
1. 下面图标中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列函数是二次函数的是( )A、 B、 C、 D、3. 已知点 , 是函数图象上的两点,且当时,有 , 则m的取值范围是( )A、 B、 C、 D、4. 如图,将绕点C顺时针方向旋转得到 , 若 , 连接 , 则等于( )
2. 下列函数是二次函数的是( )A、 B、 C、 D、3. 已知点 , 是函数图象上的两点,且当时,有 , 则m的取值范围是( )A、 B、 C、 D、4. 如图,将绕点C顺时针方向旋转得到 , 若 , 连接 , 则等于( ) A、 B、 C、 D、5. 如图,直线与双曲线交于A,B两点,若 , 则点B的坐标为( )
A、 B、 C、 D、5. 如图,直线与双曲线交于A,B两点,若 , 则点B的坐标为( ) A、 B、 C、 D、6. 如图,DC是⊙O的直径,弦AB⊥CD于M,则下列结论不一定成立的是( )
A、 B、 C、 D、6. 如图,DC是⊙O的直径,弦AB⊥CD于M,则下列结论不一定成立的是( ) A、AM=BM B、CM=DM C、 D、7. 如图,中,点D在边上, , 分别交 , , 于点E,F,G,图中相似三角形共有( ).
A、AM=BM B、CM=DM C、 D、7. 如图,中,点D在边上, , 分别交 , , 于点E,F,G,图中相似三角形共有( ). A、0对 B、1对 C、2对 D、3对8. 二次函数y=a(x-2)2+c与一次函数y=cx+a在同一坐标系中的大致图象是( )A、
A、0对 B、1对 C、2对 D、3对8. 二次函数y=a(x-2)2+c与一次函数y=cx+a在同一坐标系中的大致图象是( )A、 B、
B、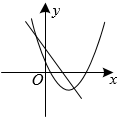 C、
C、 D、
D、
二、填空题
-
9. 已知抛物线经过点 , 则m= .10. 如图, , 分别切于点A,B, , 切于点E,交 , 于C,D两点,连接 , , 则 .
 11. 如图,抛物线与直线的两个交点坐标分别为 , , 则关于x的方程的解为 .
11. 如图,抛物线与直线的两个交点坐标分别为 , , 则关于x的方程的解为 . 12. 如图,在平行四边形中,E为边上一点,连接 , , 且与交于点 , 若 , 则 .
12. 如图,在平行四边形中,E为边上一点,连接 , , 且与交于点 , 若 , 则 . 13. 已知下列函数①;②;③ . 其中图象通过平移可以得到函数的图象的是 . (填序号)14. 如图,等边三角形和等边三角形 , 点N,点M分别为 , 的中点, , 绕点A旋转过程中,的最大值为 .
13. 已知下列函数①;②;③ . 其中图象通过平移可以得到函数的图象的是 . (填序号)14. 如图,等边三角形和等边三角形 , 点N,点M分别为 , 的中点, , 绕点A旋转过程中,的最大值为 . 15. 如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y= 的图象上.若点B在反比例函数y= 的图象上,则k的值为.
15. 如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y= 的图象上.若点B在反比例函数y= 的图象上,则k的值为.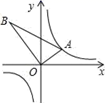 16. 如图,矩形中,P为边上一点 , . 将沿翻折得到、的延长线交边于点M,过点B作交于点N,连接 , 分别交 , 于点E,F.下面结论中:①连接 , 则;②四边形是菱形;③;④若 , 则 , 正确的结论是 .
16. 如图,矩形中,P为边上一点 , . 将沿翻折得到、的延长线交边于点M,过点B作交于点N,连接 , 分别交 , 于点E,F.下面结论中:①连接 , 则;②四边形是菱形;③;④若 , 则 , 正确的结论是 .
三、解答题
-
17. 已知关于x的一元二次方程 .(1)、若方程有实数根,求实数m的取值范围;(2)、若方程两实数根分别为和 , 且满足 , 求实数m的值.18. 如图,在矩形中,于点E,点P是边上一点,且 . 求证: .
 19. 如图,要设计一幅宽20cm,长30cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2∶3,如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?
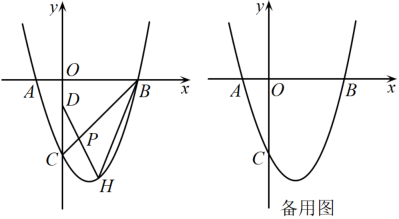
19. 如图,要设计一幅宽20cm,长30cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2∶3,如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?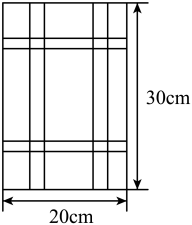 20. 如图已知收线的圆片上有三点A,B,C.
20. 如图已知收线的圆片上有三点A,B,C. (1)、作出这个圆片的圆心O(尺规作图,保留作图痕迹,不写作法);(2)、连接 , , , 设是等腰三角形,底边 , 腰 , 求该圆片的半径R.21. 如图,已知函数经过点 , 延长交双曲线另一分支于点C,过点A作直线交y轴正半轴于点D,交x轴负半轴于点E,交双曲线另一分支于点B,且 .
(1)、作出这个圆片的圆心O(尺规作图,保留作图痕迹,不写作法);(2)、连接 , , , 设是等腰三角形,底边 , 腰 , 求该圆片的半径R.21. 如图,已知函数经过点 , 延长交双曲线另一分支于点C,过点A作直线交y轴正半轴于点D,交x轴负半轴于点E,交双曲线另一分支于点B,且 . (1)、求反比例函数和直线的表达式;(2)、求的面积.22. 在中, , 点O为边的中点,连接 , 将绕点O顺时针方向旋转(旋转角为钝角),得到 , 连接 , .
(1)、求反比例函数和直线的表达式;(2)、求的面积.22. 在中, , 点O为边的中点,连接 , 将绕点O顺时针方向旋转(旋转角为钝角),得到 , 连接 , . (1)、如图1,当时,请直接写出与的数量关系(2)、如图2,延长到点D,使 , 连接 , 若 .
(1)、如图1,当时,请直接写出与的数量关系(2)、如图2,延长到点D,使 , 连接 , 若 .①求的值;
②求的长.
23. 如图,是的直径,点C,点D在上,且 , 连接、 . 连接交于点E,延长到点F,使 , 连接 . (1)、求证:是的切线;(2)、若 , 求的长.24. 某书店销售一本畅销的小说,每本进价为元.根据以往经验,当销售单价是元时,每天的销售量是本;销售单价每上涨元,每天的销售量减少本,设这本小说每天的销售量为y本,销售单价为元.(1)、请求出y与x之间的函数关系式;(2)、书店决定每销售本该小说,就捐赠元给山区贫困儿童,若想每天扣除捐赠后获得最大利润,则该小说每本售价为多少元?每天最大利润是多少元?
(1)、求证:是的切线;(2)、若 , 求的长.24. 某书店销售一本畅销的小说,每本进价为元.根据以往经验,当销售单价是元时,每天的销售量是本;销售单价每上涨元,每天的销售量减少本,设这本小说每天的销售量为y本,销售单价为元.(1)、请求出y与x之间的函数关系式;(2)、书店决定每销售本该小说,就捐赠元给山区贫困儿童,若想每天扣除捐赠后获得最大利润,则该小说每本售价为多少元?每天最大利润是多少元?