江西省赣州市寻乌县2022年九年级中考第三次模拟数学试题
试卷更新日期:2023-03-17 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、4 B、-4 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 2020年我国北斗全球卫星导航系统星座部署全面完成,北斗卫星原子钟的质量和指标授时精度相当于300万年只有1秒误差,将300万用科学记数法表示应为( )A、 B、 C、 D、4. 如图是某一立方体的侧面展开图,则该立方体是( )
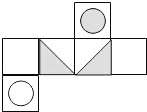 A、
A、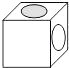 B、
B、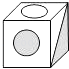 C、
C、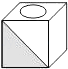 D、
D、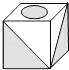 5. 七巧板是由可以错综分合的几何图案演化而来,它是一种拼板玩具,体现了我国古代劳动人民的智慧,如图1,将一块正方形薄板分为7块,其中包括5块大小不等的三角形,1块正方形和1块平行四边形,图2是由图1拼成的风车形状,则下列等式错误的是( )
5. 七巧板是由可以错综分合的几何图案演化而来,它是一种拼板玩具,体现了我国古代劳动人民的智慧,如图1,将一块正方形薄板分为7块,其中包括5块大小不等的三角形,1块正方形和1块平行四边形,图2是由图1拼成的风车形状,则下列等式错误的是( ) A、 B、 C、 D、6. 如图,一个质点在第一象限及x轴、y轴上运动,且每秒移动一个单位,在第1秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→…,若经过23秒质点到达点A,经过33秒质点到达点B,则直线AB的解析式为( )
A、 B、 C、 D、6. 如图,一个质点在第一象限及x轴、y轴上运动,且每秒移动一个单位,在第1秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→…,若经过23秒质点到达点A,经过33秒质点到达点B,则直线AB的解析式为( ) A、y=x+ B、y=-x+ C、y=2x+9 D、y=-2x+9
A、y=x+ B、y=-x+ C、y=2x+9 D、y=-2x+9二、填空题
-
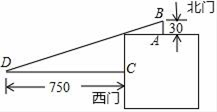
7. 分解因式:2x2-4x=.8. 已知α、β是一元二次方程x2+x-1=0的两根,则α2+2α+β-1= .9. 我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开中门,出北门三十步有木,出西门七百五十步见木,问:邑方几何?”.其大意是:如图,一座正方形城池,A为北门中点,从点A往正北方向走30步到B处有一树木,C为西门中点,从点C往正西方向走750步到D处正好看到B处的树木,则正方形城池的边长为步.
 10. 上“学习强国”学习是江老师每天的必修课,下表是江老师一周的学习得分情况:
10. 上“学习强国”学习是江老师每天的必修课,下表是江老师一周的学习得分情况:日期
1.10
1.11
1.12
1.13
1.14
1.15
1.16
得分
62
49
55
45
55
48
55
则这组数据的众数为 .
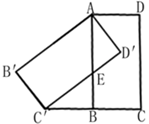
11. 如图,在中, , , 线段的垂直平分线交于点N,则的周长为 . 12. 如图,在矩形ABCD中,AB=5cm,AD=9cm,点E在边AD上运动,将△DEC沿EC翻折,使D落在D'处,若△DEC有两条边存在2倍的数关系,则D'到AD的距离为cm.
12. 如图,在矩形ABCD中,AB=5cm,AD=9cm,点E在边AD上运动,将△DEC沿EC翻折,使D落在D'处,若△DEC有两条边存在2倍的数关系,则D'到AD的距离为cm.
三、解答题
-
13.(1)、计算:(2)、如图,将矩形 绕点A顺时针旋转,得到矩形 ,点C的对应点 恰好落在 的延长线上,边 交边 于点E,求证:
 14. 先化简再求值: , 其中 .15. 小惠家大门进门处有一个三位单极开关,如图,每个开关分别控制着A(楼梯),B(客厅),C(走廊)三盏电灯,其中走廊的灯已坏(对应的开关闭合也没有亮).
14. 先化简再求值: , 其中 .15. 小惠家大门进门处有一个三位单极开关,如图,每个开关分别控制着A(楼梯),B(客厅),C(走廊)三盏电灯,其中走廊的灯已坏(对应的开关闭合也没有亮). (1)、若小惠任意闭合一个开关,“客厅灯亮了”是事件;若小惠闭合所有三个开关,“楼梯,客厅,走廊灯全亮了”是事件(填“不可能”或“必然”或“随机”);(2)、若任意闭合其中两个开关,试用画树状图或列表的方法求“客厅和楼梯灯都亮了”的概率.16. 如图,在正方形 中,请仅用无刻度直尺按下列要求作图(保留作图痕迹,不写作法).
(1)、若小惠任意闭合一个开关,“客厅灯亮了”是事件;若小惠闭合所有三个开关,“楼梯,客厅,走廊灯全亮了”是事件(填“不可能”或“必然”或“随机”);(2)、若任意闭合其中两个开关,试用画树状图或列表的方法求“客厅和楼梯灯都亮了”的概率.16. 如图,在正方形 中,请仅用无刻度直尺按下列要求作图(保留作图痕迹,不写作法). (1)、在图①中,将线段 绕点 逆时针旋转一定角度,使点 与点 重合,点 与点 重合,作出点 的位置.(2)、在图②中, 为 的中点,将 绕点 逆时针旋转某个角度,得到 ,使 与 重合,作出 .17. 为庆祝“元旦”,光明学校统一组织合唱比赛,七、八年级共92人(其中七年级的人数多于八年级的人数,且七年级的人数不足90人)准备统一购买服装参加比赛.如表是某服装厂给出服装的价格表:
(1)、在图①中,将线段 绕点 逆时针旋转一定角度,使点 与点 重合,点 与点 重合,作出点 的位置.(2)、在图②中, 为 的中点,将 绕点 逆时针旋转某个角度,得到 ,使 与 重合,作出 .17. 为庆祝“元旦”,光明学校统一组织合唱比赛,七、八年级共92人(其中七年级的人数多于八年级的人数,且七年级的人数不足90人)准备统一购买服装参加比赛.如表是某服装厂给出服装的价格表:购买服装的套数
1套至45套
46套至90套
91套以上(含91套)
每套服装的价格
60元
50元
40元
(1)、如果两个年级分别单独购买服装一共应付5000元,求七、八年级各有多少学生参加合唱比赛;(2)、如果七年级参加合唱比赛的学生中,有10名同学抽调去参加绘画比赛,不能参加合唱比赛,请你为两个年级设计一种最省钱的购买服装方案.18. 如图,在平面直角坐标系中,点B坐标是轴于点A,点B在反比例函数的图象上,将向右平移,得到交双曲线于点 . (1)、求的值;(2)、求出向右平移到的距离;(3)、连接 , 求的面积.19. 2021年, 中国航天人在太空又书写了新的奇迹. 为增进学生对航天知识的了解, 某校开展了相关的宣传教育活动. 现随机抽取部分学生进行航天知识竞赛活动, 并将所得数据绘制成如下不完整的条形统计图和扇形统计图.
(1)、求的值;(2)、求出向右平移到的距离;(3)、连接 , 求的面积.19. 2021年, 中国航天人在太空又书写了新的奇迹. 为增进学生对航天知识的了解, 某校开展了相关的宣传教育活动. 现随机抽取部分学生进行航天知识竞赛活动, 并将所得数据绘制成如下不完整的条形统计图和扇形统计图.
根据以上信息, 回答下列问题:
(1)、本次抽样的样本容量为 , “良好"所在扇形的圆心角的度数是.(2)、 补全条形统计图(3)、若该校共有学生1500人, 估计该校学生在这次竞赛中获得良好及以上的学生有多少人?20. 在日常生活中我们经常会使用到订书机,如图MN是装订机的底座,AB是装订机的托板,始终与底座平行,连接杆DE的D点固定,点E从A向B处滑动,压柄BC可绕着转轴B旋转.已知压柄BC的长度为15cm,BD=5cm,压柄与托板的长度相等. (1)、当托板与压柄夹角∠ABC=37°时,如图①点E从A点滑动了2cm,求连接杆DE的长度;(2)、当压柄BC从(1)中的位置旋转到与底座AB的夹角∠ABC=127°,如图②.求这个过程中点E滑动的距离.(答案保留根号)(参考数据:sin37°≈0.6,cos37°≈0.8.tan37°≈0.75)21. 如图,在⊙O中,直径AB垂直弦CD于E,过点A作∠DAF=∠DAB,过点D作AF的垂线,垂足为F,交AB的延长线于点P,连接CO并延长交⊙O于点G,连接EG,.
(1)、当托板与压柄夹角∠ABC=37°时,如图①点E从A点滑动了2cm,求连接杆DE的长度;(2)、当压柄BC从(1)中的位置旋转到与底座AB的夹角∠ABC=127°,如图②.求这个过程中点E滑动的距离.(答案保留根号)(参考数据:sin37°≈0.6,cos37°≈0.8.tan37°≈0.75)21. 如图,在⊙O中,直径AB垂直弦CD于E,过点A作∠DAF=∠DAB,过点D作AF的垂线,垂足为F,交AB的延长线于点P,连接CO并延长交⊙O于点G,连接EG,. (1)、求证:DF是⊙O的切线;(2)、若AD=DP,OB=3,求 的长度;(3)、若DE=4,AE=8,求线段EG的长.22. 如图1,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B在抛物线L1上(点A与点B不重合),我们把这样的两抛物线L1、L2互称为“伴随抛物线”,可见一条抛物线的“伴随抛物线”可以有多条.
(1)、求证:DF是⊙O的切线;(2)、若AD=DP,OB=3,求 的长度;(3)、若DE=4,AE=8,求线段EG的长.22. 如图1,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B在抛物线L1上(点A与点B不重合),我们把这样的两抛物线L1、L2互称为“伴随抛物线”,可见一条抛物线的“伴随抛物线”可以有多条. (1)、在图1中,抛物线:L1:y=-x2+4x-3与L2:y=a(x-4)2-3互为“伴随抛物线”,则点A的坐标为 , a的值为;(2)、在图2中,已知抛物线L3:y=2x2-8x+4,它的“伴随抛物线”为L4 , 若L3与y轴交于点C,点C关于L3的对称轴对称的对称点为D,请求出以点D为顶点的L4的解析式;(3)、若抛物线y=a1(x-m)2+n的任意一条“伴随抛物线”的解析式为y=a2(x-h)2+k,请写出a1与a2的关系式,并说明理由.23. 我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中, , 是的中线, , 垂足为 . 像这样的三角形均为“中垂三角形”.设 , , .
(1)、在图1中,抛物线:L1:y=-x2+4x-3与L2:y=a(x-4)2-3互为“伴随抛物线”,则点A的坐标为 , a的值为;(2)、在图2中,已知抛物线L3:y=2x2-8x+4,它的“伴随抛物线”为L4 , 若L3与y轴交于点C,点C关于L3的对称轴对称的对称点为D,请求出以点D为顶点的L4的解析式;(3)、若抛物线y=a1(x-m)2+n的任意一条“伴随抛物线”的解析式为y=a2(x-h)2+k,请写出a1与a2的关系式,并说明理由.23. 我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中, , 是的中线, , 垂足为 . 像这样的三角形均为“中垂三角形”.设 , , .
特例探索:
(1)、①如图1,当 , 时,a= ▲ , b= ▲ ;②如图2,当 , 时,求a和b的值.
(2)、归纳证明:请你观察(1)中的计算结果,猜想三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
(3)、利用(2)中的结论,解答下列问题:在边长为3的菱形中,O为对角线 , 的交点,分别为线段 , 的中点,连接 , 并延长交于点M, , 分别交于点G,H,如图4所示,求的值.