江苏省盐城市2022-2023学年七年级下学期第一次质量检测数学试题
试卷更新日期:2023-03-16 类型:月考试卷
一、单选题
-
1. 2022年,中国举办了第二十四届冬季奥林匹克运动会,如图,通过平移右图吉祥物“冰墩墩”可以得到的图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 如图,不能推出的条件是( )
2. 如图,不能推出的条件是( ) A、 B、 C、 D、3. 三边都不相等的三角形有两边长分别为3和5,第三长是奇数,则其周长为( )A、15 B、13 C、11 D、15或13或114. 在△ABC中,画出边AC上的高,画法正确的是( )
A、 B、 C、 D、3. 三边都不相等的三角形有两边长分别为3和5,第三长是奇数,则其周长为( )A、15 B、13 C、11 D、15或13或114. 在△ABC中,画出边AC上的高,画法正确的是( )
A、 B、
B、 C、
C、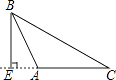 D、
D、 5. 下列各式计算正确的是( )A、 B、 C、 D、6. 如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )A、10 B、11 C、12 D、137. 在下列条件中:①∠A+∠B=∠C;②∠A:∠B:∠C=1:2:3;③∠A= ∠B= ∠C;④∠A=∠B=2∠C中,能确定△ABC为直角三角形的条件有( )A、4个 B、3个 C、2个 D、1个8. 如图,在△ABC中,∠C=90°, , 将△ABC沿直线m翻折,点A落在点D的位置,则的度数是( )
5. 下列各式计算正确的是( )A、 B、 C、 D、6. 如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )A、10 B、11 C、12 D、137. 在下列条件中:①∠A+∠B=∠C;②∠A:∠B:∠C=1:2:3;③∠A= ∠B= ∠C;④∠A=∠B=2∠C中,能确定△ABC为直角三角形的条件有( )A、4个 B、3个 C、2个 D、1个8. 如图,在△ABC中,∠C=90°, , 将△ABC沿直线m翻折,点A落在点D的位置,则的度数是( ) A、30° B、45° C、60° D、75°
A、30° B、45° C、60° D、75°二、填空题
-
9. 小明同学在百度搜索引擎中输入“中国梦,我的梦”,引擎搜索耗时0.000175秒,将这个数字用科学记数法表示为.10. 计算: .11. 一个多边形的每个外角都等于 , 则这个多边形是边形.12. 当(a-)0=1时,a的取值范围是.13. 一把直尺与一块三角板如图放置,若 , 则的度数为.
 14.
14.如图,将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为 .
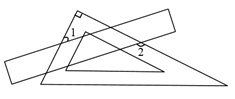
 15. 如图,把一张长方形纸片沿AB折叠,已知∠1=74°,则∠2=°;
15. 如图,把一张长方形纸片沿AB折叠,已知∠1=74°,则∠2=°; 16. 如图,点D,B,C点在同一条直线上,∠A=60°,∠C=50°,∠D=25°,则∠1=度.
16. 如图,点D,B,C点在同一条直线上,∠A=60°,∠C=50°,∠D=25°,则∠1=度.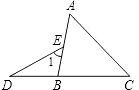 17. 若 , 则的值为.18. 当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为 .
17. 若 , 则的值为.18. 当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为 .三、解答题
-
19. 如图,在每个小正方形边长为1的方格纸中,的顶点都在方格纸格点上.

(1)将经过平移后得到 , 图中标出了点的对应点 , 补全;
(2)在图中画出的高;
(3)若连接、 , 则这两条线段之间的关系是 ▲ ;四边形的面积为 ▲ .20. 计算:(1)、;(2)、.21. 已知 , , 求下列各式的值.(1)、(2)、22. 若且 , m、n是正整数 , 则.利用上面结论解决下面的问题:(1)、如果 , 求x的值;(2)、如果 , 求x的值;23. 如图,∠BAE +∠AED=180°,∠1=∠2,那么∠M=∠N.下面是推理过程,请你完成.
解:∵∠BAE+∠AED=180°(已知)
∴AB∥DE( ).
∴∠BAE=∠AEF( ).
又∵∠1=∠2(已知)
∴ ∠BAE−∠1=∠AEF− ▲ (等式性质),即 ∠MAE = ∠NEA .
∴ ▲ ∥ ▲ ( ).
∴∠M=∠N(两直线平行,内错角相等).
24. 如图,在中, , , AD是的角平分线,求的度数. 25. 如图,在中,于点 , 于点 , .
25. 如图,在中,于点 , 于点 , .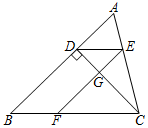 (1)、请说明DE∥BC;(2)、若∠A=60°,∠ACB=72°,求∠CDE的度数.26. 如图,在△ABC中,∠A= , ∠B= , CD是AB边上的高;CE是∠ACB的平分线,DF⊥CE于F,求∠BCE和∠CDF的度数.
(1)、请说明DE∥BC;(2)、若∠A=60°,∠ACB=72°,求∠CDE的度数.26. 如图,在△ABC中,∠A= , ∠B= , CD是AB边上的高;CE是∠ACB的平分线,DF⊥CE于F,求∠BCE和∠CDF的度数. 27. [问题背景]
27. [问题背景] (1)、如图1的图形我们把它称为“8字形”,请说理证明.(2)、[简单应用](可直接使用问题(1)中的结论)
(1)、如图1的图形我们把它称为“8字形”,请说理证明.(2)、[简单应用](可直接使用问题(1)中的结论)
如图2,、分别平分、 ,①若 , , 求的度数;
②和为任意角时,其他条件不变,试直接写出与、之间数量关系.
(3)、[问题探究]
如图3,直线平分的邻补角 , 平分∠ADC的邻补角 ,①若 , , 则的度数为 ;
②和为任意角时,其他条件不变,试直接写出与、之间数量关系.
(4)、[拓展延伸]
在图4中,若设 , , , , 试问与、之间的数量关系为;(用x、y的代数式表示)(5)、在图5中,直线平分 , 平分的外角 , 猜想与、的关系,直接写出结论.