湖南省长沙市长郡教育集团2022-2023学年九年级下学期知识梳理(月考)数学试题
试卷更新日期:2023-03-16 类型:月考试卷
一、
-
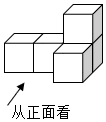
1. ﹣6的相反数是( )A、﹣6 B、﹣ C、6 D、2. 如图是由5个相同的正方体搭成的几何体,从正面看,所看到的图形是( )
 A、
A、 B、
B、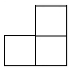 C、
C、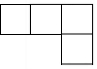 D、
D、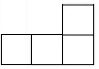 3. 神舟十三号飞船在近地点高度200000m,远地点高度356000m的轨道上驻留了6个月后,于2022年4月16日顺利返回.将数字356000用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、a2•a4=a8 B、(-2a2)3=-6a6 C、a4÷a=a3 D、2a+3a=5a25. 在平面直角坐标系中,点(a+2,2)关于原点的对称点为(4,﹣b),则ab的值为( )A、﹣4 B、4 C、12 D、﹣126. 我国古代数学名著《九章算术》记载:“今有牛五、羊二,直金十九两;牛二、羊三,直金十二两.问牛、羊各直金几何?”题目大意是:5头牛、2只羊共19两银子;2头牛、3只羊共12两银子,每头牛、每只羊各多少两银子?设1头牛两银子,1只羊两银子,则可列方程组为( )A、 B、 C、 D、7. 将直尺和三角板按如图所示的位置放置.若 , 则度数是( )
3. 神舟十三号飞船在近地点高度200000m,远地点高度356000m的轨道上驻留了6个月后,于2022年4月16日顺利返回.将数字356000用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、a2•a4=a8 B、(-2a2)3=-6a6 C、a4÷a=a3 D、2a+3a=5a25. 在平面直角坐标系中,点(a+2,2)关于原点的对称点为(4,﹣b),则ab的值为( )A、﹣4 B、4 C、12 D、﹣126. 我国古代数学名著《九章算术》记载:“今有牛五、羊二,直金十九两;牛二、羊三,直金十二两.问牛、羊各直金几何?”题目大意是:5头牛、2只羊共19两银子;2头牛、3只羊共12两银子,每头牛、每只羊各多少两银子?设1头牛两银子,1只羊两银子,则可列方程组为( )A、 B、 C、 D、7. 将直尺和三角板按如图所示的位置放置.若 , 则度数是( ) A、 B、 C、 D、8. 已知点 , 在反比例函数的图象上,且 , 则下列结论一定正确的是( )A、 B、 C、 D、9. 如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠CAB=65°,则∠ADC的度数为( )
A、 B、 C、 D、8. 已知点 , 在反比例函数的图象上,且 , 则下列结论一定正确的是( )A、 B、 C、 D、9. 如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠CAB=65°,则∠ADC的度数为( )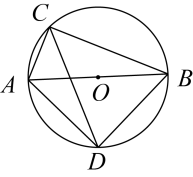 A、25° B、35° C、45° D、65°10. 如图,正方形ABCD的边长为 , 直线EF经过正方形的中心O,并能绕着O转动,分别交AB、CD边于E、F点,过点B作直线EF的垂线BG,垂足为点G,连接AG,则AG长的最小值为( )
A、25° B、35° C、45° D、65°10. 如图,正方形ABCD的边长为 , 直线EF经过正方形的中心O,并能绕着O转动,分别交AB、CD边于E、F点,过点B作直线EF的垂线BG,垂足为点G,连接AG,则AG长的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算: = .12. 甲、乙两人在相同条件下进行射击练习,每人10次射击战绩的平均数都是8环,方差分别为 , 则两人射击成绩比较稳定的是(填“甲”或“乙”).13. 如图,平行四边形中,E为延长线上的一点,且 , 交于点F.若 , 则的长为.
 14. 如图,河坝横断面迎水坡的坡比是(坡比是坡面的铅直高度与水平宽度之比),水平宽度 , 则坡面的长度是m.
14. 如图,河坝横断面迎水坡的坡比是(坡比是坡面的铅直高度与水平宽度之比),水平宽度 , 则坡面的长度是m. 15. 将抛物线向下平移3个单位长度,再向左平移2个单位长度,得到抛物线的表达式为.16. 如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为 .
15. 将抛物线向下平移3个单位长度,再向左平移2个单位长度,得到抛物线的表达式为.16. 如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为 .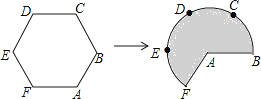
三、解答题
-
17. 计算:.18. 已知 ,求代数式 的值.19. 解方程:20. 某校为了解九年级学生体质健康情况,随机抽取了部分学生进行体能测试,根据测试结果绘制了不完整的条形统计图和扇形统计图,请回答下列问题:
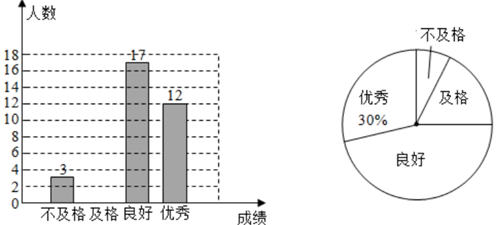 (1)、在这次调查中,“优秀”所在扇形的圆心角的度数是;(2)、请补全条形统计图;(3)、若该校九年级共有学生1200人,则估计该校“良好”的人数是;(4)、已知“不合格”的3名学生中有2名男生、1名女生,如果从中随机抽取两名同学进行体能加试,请用列表法或画树状图的方法,求抽到两名男生的概率多少?21. 如图,在平面直角坐标系中,一次函数的图象与轴、轴分别交于、两点,且 , 与反比例函数的图象交于 , 两点.
(1)、在这次调查中,“优秀”所在扇形的圆心角的度数是;(2)、请补全条形统计图;(3)、若该校九年级共有学生1200人,则估计该校“良好”的人数是;(4)、已知“不合格”的3名学生中有2名男生、1名女生,如果从中随机抽取两名同学进行体能加试,请用列表法或画树状图的方法,求抽到两名男生的概率多少?21. 如图,在平面直角坐标系中,一次函数的图象与轴、轴分别交于、两点,且 , 与反比例函数的图象交于 , 两点.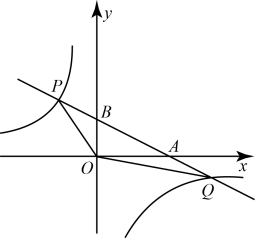 (1)、求该反比例函数的解析式;(2)、求的面积;(3)、请根据图象直接写出不等式的解集.22. 2022年北京冬季奥运会在北京市和张家口市联合举行,冬奥会吉祥物为“冰墩墩”.(1)、据市场调研发现,某工厂今年二月份共生产500个“冰墩墩”,为增大生产量,该工厂平均每月生产量增长率相同,四月份该工厂生产了720个“冰墩墩”,求该工厂平均每月生产量增长率是多少?(2)、已知某商店“冰墩墩”平均每天可销售20个,每个盈利40元,在每个降价幅度不超过10元的情况下,每降价1元,则每天可多售5件.若每天要盈利1440元,则每个“冰墩墩”应降价多少元?23. 如图,在菱形ABCD中,AB=2,∠ABC=60°,点E是AB边上的一个动点,连接CE,点F在边AB的延长线上,且BF=BE,连接DF交CE于点G,连接BG.
(1)、求该反比例函数的解析式;(2)、求的面积;(3)、请根据图象直接写出不等式的解集.22. 2022年北京冬季奥运会在北京市和张家口市联合举行,冬奥会吉祥物为“冰墩墩”.(1)、据市场调研发现,某工厂今年二月份共生产500个“冰墩墩”,为增大生产量,该工厂平均每月生产量增长率相同,四月份该工厂生产了720个“冰墩墩”,求该工厂平均每月生产量增长率是多少?(2)、已知某商店“冰墩墩”平均每天可销售20个,每个盈利40元,在每个降价幅度不超过10元的情况下,每降价1元,则每天可多售5件.若每天要盈利1440元,则每个“冰墩墩”应降价多少元?23. 如图,在菱形ABCD中,AB=2,∠ABC=60°,点E是AB边上的一个动点,连接CE,点F在边AB的延长线上,且BF=BE,连接DF交CE于点G,连接BG. (1)、当点E是AB的中点时,求CE的长;(2)、在(1)的条件下,求BG的长;(3)、当BG时,请直接写出线段AF的长.24. 我们把纵坐标是横坐标两倍的点叫双语点,如点 , 点.(1)、函数的双语点是;(2)、函数(k为常数,目)上是否存在双语点?若存在,求出双语点的坐标,若不存在,请说明理由;(3)、函数的图象上只有唯一一个双语点,且当时,m的最小值为k,求实数k的值.25. 如图,在平面直角坐标系中,为原点,已知点是射线上一点, , 点是轴正半轴上一点, , 连接 , 经过点且与相切于点 , 与边相交于另一点.
(1)、当点E是AB的中点时,求CE的长;(2)、在(1)的条件下,求BG的长;(3)、当BG时,请直接写出线段AF的长.24. 我们把纵坐标是横坐标两倍的点叫双语点,如点 , 点.(1)、函数的双语点是;(2)、函数(k为常数,目)上是否存在双语点?若存在,求出双语点的坐标,若不存在,请说明理由;(3)、函数的图象上只有唯一一个双语点,且当时,m的最小值为k,求实数k的值.25. 如图,在平面直角坐标系中,为原点,已知点是射线上一点, , 点是轴正半轴上一点, , 连接 , 经过点且与相切于点 , 与边相交于另一点.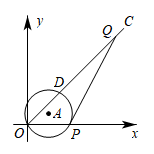 (1)、若圆心在轴上,求的半径;(2)、若圆心在轴的上方,且圆心到轴的距离为 , 求的半径;(3)、在(2)的条件下,若 , 点是经过点 , , 的抛物线上的一个动点,点为轴上的一个动点,若满足的点共有个,求点的横坐标的取值范围.
(1)、若圆心在轴上,求的半径;(2)、若圆心在轴的上方,且圆心到轴的距离为 , 求的半径;(3)、在(2)的条件下,若 , 点是经过点 , , 的抛物线上的一个动点,点为轴上的一个动点,若满足的点共有个,求点的横坐标的取值范围.