湖北省随州市广水市2022-2023学年九年级下学期第一阶段考试数学试卷
试卷更新日期:2023-03-16 类型:月考试卷
一、单选题
-
1. −2023的绝对值是( )A、−2023 B、2023 C、±2023 D、2. 正方形广场的边长为 , 其面积用科学记数法表示为( )A、 B、 C、 D、3. 如图,分别是三边的中点,若 , , 则的度数为( )
 A、 B、 C、 D、4. 下列计算中,正确的是( )A、 B、 C、 D、5. 三个大小一样的正方体按如图摆放,它的主视图是( )
A、 B、 C、 D、4. 下列计算中,正确的是( )A、 B、 C、 D、5. 三个大小一样的正方体按如图摆放,它的主视图是( )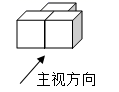 A、
A、 B、
B、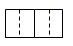 C、
C、 D、
D、 6. 在体育中考中,某中学九(1)班仰卧起坐成绩为良好的学生有15人,分布情况如下表所示,其成绩的众数和中位数分别是( )
6. 在体育中考中,某中学九(1)班仰卧起坐成绩为良好的学生有15人,分布情况如下表所示,其成绩的众数和中位数分别是( )成绩/个
42
43
44
45
46
47
人数
1
3
2
2
5
2
A、5,2 B、46,45 C、5,7 D、45,44.57. 我国古代数学名著《张丘建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗,今持粟三斛,得酒五斗,问清、醑酒各几何?”意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清、醑酒各几斗,设清洒有斗,那么可列方程为( )A、 B、 C、 D、8. 如图,△ABC中,BC=6,BC边上的高为3,点D,E,F分别在边BC,AB,AC上,且EF∥BC.设点E到BC的距离为x,△DEF的面积为y,则y关于x的函数图象大致是( )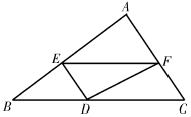 A、
A、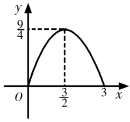 B、
B、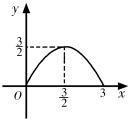 C、
C、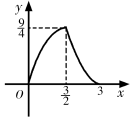 D、
D、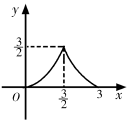 9. 在平面直角坐标系中,点经过某种变换后得到点 , 我们把点叫做点的终结点,已知点的终结点为 , 点的终结点为 , 点的终结点为 , 这样由依次得到 , 若点的坐标为 , 则点的坐标为( )A、 B、 C、 D、10. 如图,抛物线的对称轴是 , 并与x轴交于A,B两点,若 , 则下列结论中:①;②;③;④若m为任意实数,则 , 正确的个数是( )
9. 在平面直角坐标系中,点经过某种变换后得到点 , 我们把点叫做点的终结点,已知点的终结点为 , 点的终结点为 , 点的终结点为 , 这样由依次得到 , 若点的坐标为 , 则点的坐标为( )A、 B、 C、 D、10. 如图,抛物线的对称轴是 , 并与x轴交于A,B两点,若 , 则下列结论中:①;②;③;④若m为任意实数,则 , 正确的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 计算:.12. 定义一种新运算:对于任意非零实数 , , , 若 , 则的值为.13. 如图,是的直径, , 则.
 14. 如图,小明在时测得某树的影长为 , 时又测得该树的影长为 , 若两次日照的光线互相垂直,则树的高度为.
14. 如图,小明在时测得某树的影长为 , 时又测得该树的影长为 , 若两次日照的光线互相垂直,则树的高度为. 15. 如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD, , 则k= .
15. 如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD, , 则k= .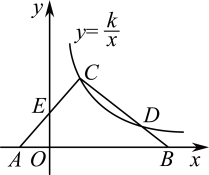 16. 如图,在矩形中, , , 点分别是上的动点,点不与重合,且 , 点是五边形内点, , 且.
16. 如图,在矩形中, , , 点分别是上的动点,点不与重合,且 , 点是五边形内点, , 且.
①当点为的中点时,.
②点到边距离为 , 则的取值范围为.
三、解答题
-
17. 先化简, , 再从的整数中选取一个你喜欢的的值代入求值.18. 已知、是关于的一元二次方程的两个实数根.(1)、求的取值范围;(2)、是否存在实数根 , 使成立,若存在,求出的值,若不存在,请说明理由.19. 如图,在 中,过点 作 于点 ,点 在边 上, .连接 , .
 (1)、求证:四边形 是矩形;(2)、若 , 平分 , ,则四边形 的周长是 .20. 据网站调查,2022年网民们关注的热点话题分别有:消费、教育、环保、反腐及其他共五类,根据调查的部分相关数据,绘制的统计图表如下:
(1)、求证:四边形 是矩形;(2)、若 , 平分 , ,则四边形 的周长是 .20. 据网站调查,2022年网民们关注的热点话题分别有:消费、教育、环保、反腐及其他共五类,根据调查的部分相关数据,绘制的统计图表如下: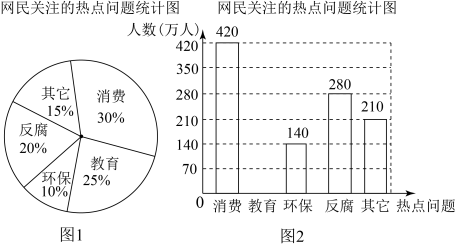 (1)、求出共调查了多少人,并补全条形统计图;(2)、若某市约有880万人口,请你估计最关注环保问题的人数约为多少万人?(3)、在这次调查中,某单位共有里、乙、丙、丁四人最关注教育问题,现准备从这四大中随机抽取两人进行座谈,试用列表法或树形图的方法抽取的两人恰好是甲和乙的概率.21. 如图,D是以AB为直径的⊙O上一点,过点D的切线DE交AB的延长线于点E,过点B作BC⊥DE交AD的延长线于点C,垂足为点F.
(1)、求出共调查了多少人,并补全条形统计图;(2)、若某市约有880万人口,请你估计最关注环保问题的人数约为多少万人?(3)、在这次调查中,某单位共有里、乙、丙、丁四人最关注教育问题,现准备从这四大中随机抽取两人进行座谈,试用列表法或树形图的方法抽取的两人恰好是甲和乙的概率.21. 如图,D是以AB为直径的⊙O上一点,过点D的切线DE交AB的延长线于点E,过点B作BC⊥DE交AD的延长线于点C,垂足为点F.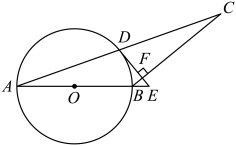 (1)、求证:AB=CB;(2)、若AB=18,sinA= , 求EF的长.22. 襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).(1)、m= , n=;(2)、求销售蓝莓第几天时,当天的利润最大?最大利润是多少?(3)、在销售蓝莓的30天中,当天利润不低于870元的共有多少天?23. 阅读下面材料.
(1)、求证:AB=CB;(2)、若AB=18,sinA= , 求EF的长.22. 襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).(1)、m= , n=;(2)、求销售蓝莓第几天时,当天的利润最大?最大利润是多少?(3)、在销售蓝莓的30天中,当天利润不低于870元的共有多少天?23. 阅读下面材料.小炎遇到这个一个问题:如图1,点E、F分别在正方形的边上, , 连接 , 则 , 试说明理由.
小炎是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中,她先尝试了翻折、旋转、平移的方法,最后发现线段是共点并且相等的,于是找到解决问题的方法.她的方法是将绕着点A逆时针旋转90°得到 , 再利用全等的知识解决这个问题(如图2).
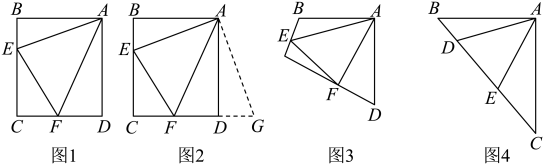
参考小炎同学思考问题的方法,解决下列问题:
(1)、写出小炎的推理过程;(2)、如图3,四边形ABCD中, , , 点E、F分别在边上, , 若、都不是直角,则当与满足于关系时,仍有;(3)、如图4,在中, , , 点D、E均在边BC上,且 , 若 , , 求DE的长.24. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点C,抛物线的对称轴是直线 , 且经过A、C两点与x轴的另一交点为B. (1)、①直接写出点B的坐标;②求抛物线的解析式;(2)、点E为直线上方抛物线上的一动点,过点E作x轴于点G,交于点D,连接 , 当四边形面积最大时,求出E点的坐标.(3)、抛物线上是否存在点M,过点M作轴于点N,使得以点A、M、N为顶点的与相似?若存在,直接写出点M的坐标,若不存在,请说明理由.
(1)、①直接写出点B的坐标;②求抛物线的解析式;(2)、点E为直线上方抛物线上的一动点,过点E作x轴于点G,交于点D,连接 , 当四边形面积最大时,求出E点的坐标.(3)、抛物线上是否存在点M,过点M作轴于点N,使得以点A、M、N为顶点的与相似?若存在,直接写出点M的坐标,若不存在,请说明理由.