湖北省黄石市2022-2023学年九年级下学期三月调考数学试卷
试卷更新日期:2023-03-16 类型:月考试卷
一、单选题
-
1. -2022的绝对值是( )A、 B、 C、-2022 D、20222. 下面图形中既是轴对称图形又是中心对称图形的是( )
 A、科克曲线 B、笛卡尔心形线 C、阿基米德螺旋线 D、赵爽弦图3. 由七个相同的小立方块搭成的几何体如图所示,则它的主视图是( )
A、科克曲线 B、笛卡尔心形线 C、阿基米德螺旋线 D、赵爽弦图3. 由七个相同的小立方块搭成的几何体如图所示,则它的主视图是( )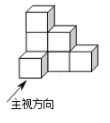 A、
A、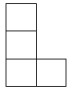 B、
B、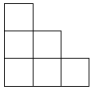 C、
C、 D、
D、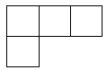 4. 下列运算正确的是( )A、 B、 C、 D、5. 代数式有意义,则的取值范围是( )A、 B、 C、且 D、且6. 开学前,根据学校防疫要求,小宁同学连续14天进行了体温测量,结果统计如下表:
4. 下列运算正确的是( )A、 B、 C、 D、5. 代数式有意义,则的取值范围是( )A、 B、 C、且 D、且6. 开学前,根据学校防疫要求,小宁同学连续14天进行了体温测量,结果统计如下表:体温()
36.2
36.3
36.5
36.6
36.8
天数(天)
3
3
4
2
2
这14天中,小宁体温的众数和中位数分别为( )
A、 , B、 , C、 , D、 ,7. 如图,点A的坐标为 ,点B是x轴正半轴上的一点,将线段AB绕点A按逆时针方向旋转60°得到线段AC.若点C的坐标为 ,则m的值为( )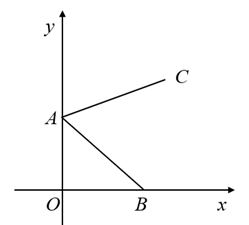 A、 B、 C、 D、8. 如图,在 中,分别以点 和点 为圆心,大于 长为半径画弧,两弧相交于点 , .作直线 ,交 于点 ,交 于点 ,连接 .若 , , ,则 的周长为( )
A、 B、 C、 D、8. 如图,在 中,分别以点 和点 为圆心,大于 长为半径画弧,两弧相交于点 , .作直线 ,交 于点 ,交 于点 ,连接 .若 , , ,则 的周长为( )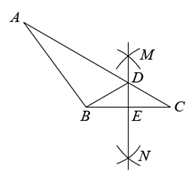 A、25 B、22 C、19 D、189. 有一个计算程序,每次运算都是把一个数先乘以2,再除以它与1的和,多次重复进行这种运算的过程如下:
A、25 B、22 C、19 D、189. 有一个计算程序,每次运算都是把一个数先乘以2,再除以它与1的和,多次重复进行这种运算的过程如下:
若输入的值为 ,则 的值为( )
A、 B、 C、 D、10. 已知二次函数与x轴交于A,B两点,与y轴交于点C.下列说法正确的是( )①线段的长度为;②抛物线的对称轴为直线;③P是此抛物线的对称轴上的一个动点,当P点坐标为时,的值最大;④若M是x轴上的一个动点,N是此抛物线上的一个动点,如果以A,C,M,N为顶点的四边形是平行四边形,满足条件的M点有4个.
 A、①② B、①②③ C、①②④ D、③④
A、①② B、①②③ C、①②④ D、③④二、填空题
-
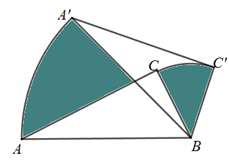
11. 计算:.12. 因式分解:13. 新型冠状病毒2019(HCoV-19),它的形状是一个球体,体积大约 , 将数864000用科学记数法表示为.14. 关于x的分式方程的解为正数,则a的取值范围是 .15. 如图,在 中, , , . 绕点B顺时针方向旋转45°得到 ,点A经过的路径为弧 ,点C经过的路径为弧 ,则图中阴影部分的面积为.(结果保留 )
 16. 在数学实践活动课上,某兴趣小组测量操场上篮球筐距地面的高度如图所示,已知篮球筐的直径AB约为0.45m,某同学站在C处,先仰望篮球筐直径的一端A处,测得仰角为42°,再调整视线,测得篮球筐直径的另一端B处的仰角为35°.若该同学的目高OC为1.7m,则篮球筐距地面的高度AD大约是m.(结果精确到1m).(参考数据:tan42°≈0.9,tan35°=0.7,tan48°≈1.1,tan55°≈1.4)
16. 在数学实践活动课上,某兴趣小组测量操场上篮球筐距地面的高度如图所示,已知篮球筐的直径AB约为0.45m,某同学站在C处,先仰望篮球筐直径的一端A处,测得仰角为42°,再调整视线,测得篮球筐直径的另一端B处的仰角为35°.若该同学的目高OC为1.7m,则篮球筐距地面的高度AD大约是m.(结果精确到1m).(参考数据:tan42°≈0.9,tan35°=0.7,tan48°≈1.1,tan55°≈1.4)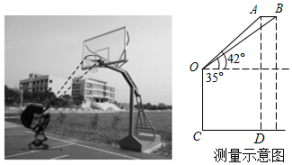 17. 如图,为等边三角形,点的坐标为 , 过点作直线交于 , 交于 , 点在反比例函数的图像上,当和的面积相等时,的值是.
17. 如图,为等边三角形,点的坐标为 , 过点作直线交于 , 交于 , 点在反比例函数的图像上,当和的面积相等时,的值是. 18. 如图,在边长为2的正方形ABCD中,点E,F分别是边BC,AD上的点,连接EF,将四边形ABEF沿EF折叠,点B的对应点G恰好落在CD边上,点A的对应点为H,连接BH.则 的最小值是 .
18. 如图,在边长为2的正方形ABCD中,点E,F分别是边BC,AD上的点,连接EF,将四边形ABEF沿EF折叠,点B的对应点G恰好落在CD边上,点A的对应点为H,连接BH.则 的最小值是 .
三、解答题
-
19. 先化简,再求值: , 其中从 , , 三个数中任取一个合适的值.20. 如图,中,点D是边上一点,点E是的中点,过点C作交的延长线于点F.
 (1)、求证:;(2)、若 , , 求的度数.21. 某学校准备组织学生参加唱歌、舞蹈、书法、朗诵活动,为了解学生的参与情况,该校随机抽取了部分学生进行“你愿意参加哪一项活动”(必选且只选一种)的问卷调查.根据调查结果绘制了两幅不完整的统计图,请根据图中信息,解答下列问题:
(1)、求证:;(2)、若 , , 求的度数.21. 某学校准备组织学生参加唱歌、舞蹈、书法、朗诵活动,为了解学生的参与情况,该校随机抽取了部分学生进行“你愿意参加哪一项活动”(必选且只选一种)的问卷调查.根据调查结果绘制了两幅不完整的统计图,请根据图中信息,解答下列问题: (1)、本次抽样调查的总人数为 , 扇形统计图中“舞蹈”对应的圆心角的度数为.(2)、若该校有1400名学生,估计选择参加“书法”的有多少人?(3)、学校准备从推荐的4位同学(两男两女)中随机选取两人当正式活动的主持人,利用画树状图法或列表法求选取的两人恰为一男一女的概率.22. 阅读材料:
(1)、本次抽样调查的总人数为 , 扇形统计图中“舞蹈”对应的圆心角的度数为.(2)、若该校有1400名学生,估计选择参加“书法”的有多少人?(3)、学校准备从推荐的4位同学(两男两女)中随机选取两人当正式活动的主持人,利用画树状图法或列表法求选取的两人恰为一男一女的概率.22. 阅读材料:材料1:若一元二次方程的两个根为 , 则 , .
材料2:已知实数 , 满足 , , 且 , 求的值.
解:由题知 , 是方程的两个不相等的实数根,根据材料1得 , , 所以
根据上述材料解决以下问题:
(1)、材料理解:一元二次方程的两个根为 , , 则 , .(2)、类比探究:已知实数 , 满足 , , 且 , 求的值.(3)、思维拓展:已知实数、分别满足 , , 且.求的值.23. 星星服装厂生产A品牌服装,每件成本为68元,零售商到星星服装厂一次性批发A品牌服装件,批发单价为y元,y与x之间满足如图所示的函数关系. (1)、求y与x的函数关系式;(2)、零售商到星星服装厂一次性批发A品牌服装件,服装厂的利润为w元,问x为何值时,w最大?最大值是多少?(3)、零售商到星星服装厂一次性批发A品牌服装x件,若星星服装厂欲获利不低于4320元,请直接写出x的取值范围.24. 如图,是的直径,点是上异于、的一点,点是角平分线上一点,连接、 , 其中交于点 , 交于点 , 且点是的中点.
(1)、求y与x的函数关系式;(2)、零售商到星星服装厂一次性批发A品牌服装件,服装厂的利润为w元,问x为何值时,w最大?最大值是多少?(3)、零售商到星星服装厂一次性批发A品牌服装x件,若星星服装厂欲获利不低于4320元,请直接写出x的取值范围.24. 如图,是的直径,点是上异于、的一点,点是角平分线上一点,连接、 , 其中交于点 , 交于点 , 且点是的中点. (1)、求证:直线是的切线;(2)、若点是的中点,求的值;(3)、若 , , 求的长.25. 如图,在平面直角坐标系xOy中,抛物线 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
(1)、求证:直线是的切线;(2)、若点是的中点,求的值;(3)、若 , , 求的长.25. 如图,在平面直角坐标系xOy中,抛物线 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.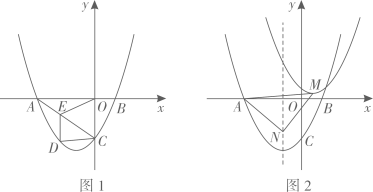 (1)、求点A的坐标;(2)、如图1,连接AC,点D为线段AC下方抛物线上一动点,过点D作DE∥y轴交线段AC于E点,连接EO,记△ADC的面积为 ,△AEO的面积为 ,求 的最大值及此时点D的坐标;(3)、如图2,将抛物线沿射线CB方向平移 个单位长度得到新抛物线,动点N在原抛物线的对称轴上,点M为新抛物线的顶点,当△AMN为以AM为腰的等腰三角形时,请直接写出点N的坐标.
(1)、求点A的坐标;(2)、如图1,连接AC,点D为线段AC下方抛物线上一动点,过点D作DE∥y轴交线段AC于E点,连接EO,记△ADC的面积为 ,△AEO的面积为 ,求 的最大值及此时点D的坐标;(3)、如图2,将抛物线沿射线CB方向平移 个单位长度得到新抛物线,动点N在原抛物线的对称轴上,点M为新抛物线的顶点,当△AMN为以AM为腰的等腰三角形时,请直接写出点N的坐标.