(人教版)2022-2023学年九年级数学下册28.2 解直角三角形及其应用 同步测试
试卷更新日期:2023-03-16 类型:同步测试
一、单选题
-
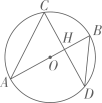
1. 如图,AB是⊙O的直径,且经过弦CD的中点H,已知cos∠CDB= , BD=5,则OH的长为( )
 A、 B、 C、1 D、2. 将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是( )
A、 B、 C、1 D、2. 将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是( )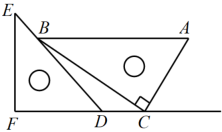 A、5 B、 C、10- D、15-3. 在Rt△ABC中,∠C=90° , BC=6,sinA= , 则AB=( )A、8 B、9 C、10 D、124. 如图是大坝的横断面,斜坡AB的坡度 i1 =1:2,背水坡CD的坡度i2=1:1,若坡面CD的长度为 米,则斜坡AB的长度为( )
A、5 B、 C、10- D、15-3. 在Rt△ABC中,∠C=90° , BC=6,sinA= , 则AB=( )A、8 B、9 C、10 D、124. 如图是大坝的横断面,斜坡AB的坡度 i1 =1:2,背水坡CD的坡度i2=1:1,若坡面CD的长度为 米,则斜坡AB的长度为( )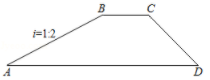 A、 B、 C、 D、245. 已知一道斜坡的坡比为1: ,坡长为24米,那么坡高为( )米.A、 B、12 C、 D、66. 如图,滑雪场有一坡角为20°的滑道,滑雪道的长AC为100米,则BC的长为( )米.
A、 B、 C、 D、245. 已知一道斜坡的坡比为1: ,坡长为24米,那么坡高为( )米.A、 B、12 C、 D、66. 如图,滑雪场有一坡角为20°的滑道,滑雪道的长AC为100米,则BC的长为( )米. A、 B、100cos20° C、 D、100sin20°7. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC .若 AB=BC=1,∠AOB=α,则 OC2的值为( )
A、 B、100cos20° C、 D、100sin20°7. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC .若 AB=BC=1,∠AOB=α,则 OC2的值为( )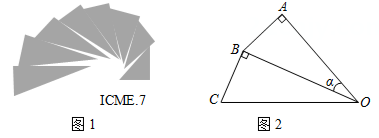 A、 B、 C、 D、8. 春节期间,某老师读到《行路难》中“闲来垂钓碧溪上,忽复乘舟梦日边.”邀约好友一起在江边垂钓,如图,河堤AB的坡度为1:2.4,AB长为5.2米,钓竿AC与水平线的夹角是60°,其长为6米,若钓竿AC与钓鱼线CD的夹角也是60°,则浮漂D与河堤下端B之间的距离约为( )(参考数据: =1.732)
A、 B、 C、 D、8. 春节期间,某老师读到《行路难》中“闲来垂钓碧溪上,忽复乘舟梦日边.”邀约好友一起在江边垂钓,如图,河堤AB的坡度为1:2.4,AB长为5.2米,钓竿AC与水平线的夹角是60°,其长为6米,若钓竿AC与钓鱼线CD的夹角也是60°,则浮漂D与河堤下端B之间的距离约为( )(参考数据: =1.732) A、2.33米 B、2.35米 C、2.36米 D、2.42米9. 在Rt△ABC中,∠C=90°,sinA= ,BC=6,则AB长是( )A、4 B、6 C、8 D、1010. 如图,热气球探测器显示,从热气球A处看一栋楼顶部B处的仰角α为30°,看这栋楼底部C处的俯角β为60°,热气球与楼的水平距离AD为90米,则这栋楼的高度BC为( )
A、2.33米 B、2.35米 C、2.36米 D、2.42米9. 在Rt△ABC中,∠C=90°,sinA= ,BC=6,则AB长是( )A、4 B、6 C、8 D、1010. 如图,热气球探测器显示,从热气球A处看一栋楼顶部B处的仰角α为30°,看这栋楼底部C处的俯角β为60°,热气球与楼的水平距离AD为90米,则这栋楼的高度BC为( )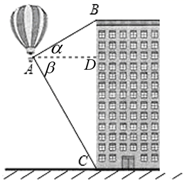 A、 米 B、90 米 C、120 米 D、225米
A、 米 B、90 米 C、120 米 D、225米二、填空题
-
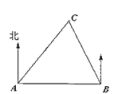
11. 如图,在一笔直的海岸线上有、两个观测站,在的正西方向,km,从测得船在北偏东45°的方向,从测得船在北偏西30°的方向,则船离海岸线的距离是.
 12. 如果一个正六边形的边心距的长度为 , 那么它的半径的长度为cm.13. 如图,在中,弦的长为 , 圆心到弦的距离为6,则的度数为.
12. 如果一个正六边形的边心距的长度为 , 那么它的半径的长度为cm.13. 如图,在中,弦的长为 , 圆心到弦的距离为6,则的度数为.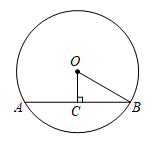 14. 某通信公司准备逐步在山上建设5G基站.如图,某处斜坡的坡角的正切值为 , 通讯塔垂直于水平地面,在C处测得塔顶A的仰角为45°,在D处测得塔顶A的仰角为53°,斜坡路段长26米则通讯塔的高度约为米.(参考数据: , , )
14. 某通信公司准备逐步在山上建设5G基站.如图,某处斜坡的坡角的正切值为 , 通讯塔垂直于水平地面,在C处测得塔顶A的仰角为45°,在D处测得塔顶A的仰角为53°,斜坡路段长26米则通讯塔的高度约为米.(参考数据: , , )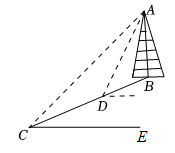 15. 如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.则大楼AB的高度 .(结果保留根号)
15. 如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.则大楼AB的高度 .(结果保留根号)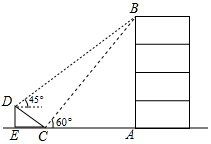
三、解答题
-
16. 为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)i=1:2.4的山坡AB上发现有一棵古树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为多少米?(参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11)
 17. 某数学兴趣小组通过调查研究把“如何测量嵩岳寺塔的高度”作为一项课题活动,他们制订了测量方案,并利用课余时间实地测量.
17. 某数学兴趣小组通过调查研究把“如何测量嵩岳寺塔的高度”作为一项课题活动,他们制订了测量方案,并利用课余时间实地测量.课题
测量嵩岳寺塔的高度
测量工具
测量角度的仪器,皮尺等
测量方案
在点 处放置高为 米的测角仪 ,此时测得塔顶端 的仰角为 ,再沿 方向走 米到达点 处,此时测得塔顶端 的仰角为 .
说明: 、 、 三点在同一水平线上
请你根据表中信息结合示意图帮助该数学兴趣小组求嵩岳寺塔 的高度.
精确到0.1米,参考数据: , ,
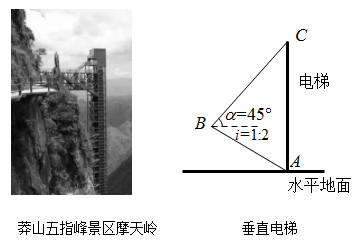
 18. 如图,莽山五指峰景区新建了一座垂直观光电梯.某测绘兴趣小组为测算电梯的高度,测得斜坡米,坡度 , 在处测得电梯顶端的仰角 , 求观光电梯的高度.
18. 如图,莽山五指峰景区新建了一座垂直观光电梯.某测绘兴趣小组为测算电梯的高度,测得斜坡米,坡度 , 在处测得电梯顶端的仰角 , 求观光电梯的高度.(参考数据: , , . 结果精确到0.1米)
四、综合题
-
19. 为进一步加强疫情防控工作,避免在测温过程中出现人员聚集现象,某学校决定安装红外线体温检测仪,该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温(如图1),其红外线探测点可以在垂直于地面的支杆上下调节(如图2),已知探测最大角为 , 探测最小角为 .
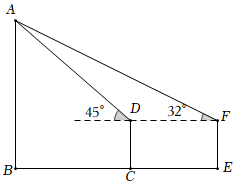
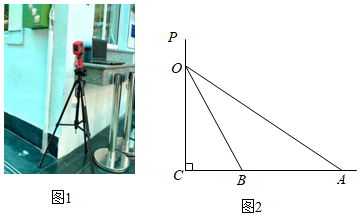 (1)、若该设备的安装高度为1.6米时,求测温区域的宽度 .(2)、该校要求测温区域的宽度为2.53米,请你帮助学校确定该设备的安装高度 . (结果精确到0.01米,参考数据: , , , , , )20. 为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度AB,他站在距离教学楼底部E处6米远的地面C处,测得宣传牌的底部B的仰角为60°,同时测得教学楼窗户D处的仰角为30°(A、B、D、E在同一直线上).然后,小明沿坡度i=1:1.5的斜坡从C走到F处,此时DF正好与地面CE平行.
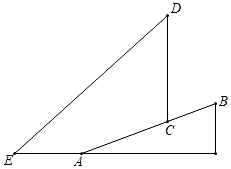
(1)、若该设备的安装高度为1.6米时,求测温区域的宽度 .(2)、该校要求测温区域的宽度为2.53米,请你帮助学校确定该设备的安装高度 . (结果精确到0.01米,参考数据: , , , , , )20. 为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度AB,他站在距离教学楼底部E处6米远的地面C处,测得宣传牌的底部B的仰角为60°,同时测得教学楼窗户D处的仰角为30°(A、B、D、E在同一直线上).然后,小明沿坡度i=1:1.5的斜坡从C走到F处,此时DF正好与地面CE平行. (1)、求点F到直线CE的距离(结果保留根号);(2)、若小明在F处又测得宣传牌顶部A的仰角为45°,求宣传牌的高度AB(结果精确到0.1米,≈1.41,≈1.73).21. 在一次课外活动中,某数学兴趣小组测量一棵树CD的高度.如图所示,测得斜坡BE的坡度i=1:4(即AB:AE=1:4),坡底AE的长为8米,在B处测得树CD顶部D的仰角为30°,在E处测得树CD顶部D的仰角为60°.
(1)、求点F到直线CE的距离(结果保留根号);(2)、若小明在F处又测得宣传牌顶部A的仰角为45°,求宣传牌的高度AB(结果精确到0.1米,≈1.41,≈1.73).21. 在一次课外活动中,某数学兴趣小组测量一棵树CD的高度.如图所示,测得斜坡BE的坡度i=1:4(即AB:AE=1:4),坡底AE的长为8米,在B处测得树CD顶部D的仰角为30°,在E处测得树CD顶部D的仰角为60°.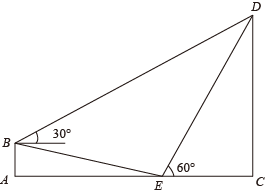 (1)、求AB的高;(2)、求树高CD.(结果保留根号)22. 如图,已知AB是⊙O的直径,弦CD与直径AB相交于点F.点E在⊙O外,作直线AE,且∠EAC=∠D.
(1)、求AB的高;(2)、求树高CD.(结果保留根号)22. 如图,已知AB是⊙O的直径,弦CD与直径AB相交于点F.点E在⊙O外,作直线AE,且∠EAC=∠D.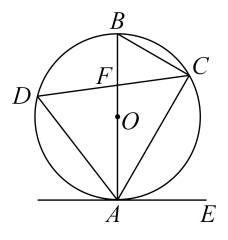 (1)、求证:直线AE是⊙O的切线.(2)、若∠BAC=30°,BC=4,cos∠BAD= , 求BF的长.23. 如图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图,量得托板长 , 支撑板长 , 底座长 , 托板固定在支撑板顶端点处,且 , 托板可绕点转动,支撑板可绕点转动.(结果保留小数点后一位)(参考数据: , , , , )
(1)、求证:直线AE是⊙O的切线.(2)、若∠BAC=30°,BC=4,cos∠BAD= , 求BF的长.23. 如图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图,量得托板长 , 支撑板长 , 底座长 , 托板固定在支撑板顶端点处,且 , 托板可绕点转动,支撑板可绕点转动.(结果保留小数点后一位)(参考数据: , , , , )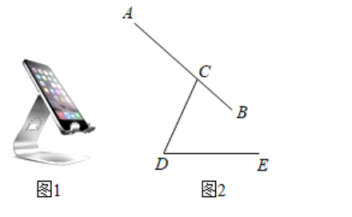 (1)、若 , , 求点到直线的距离;(2)、为了观看舒适,在(1)的情况下,把绕点逆时针旋转后,再将绕点顺时针旋转,使点落在直线上即可,求旋转的角度.
(1)、若 , , 求点到直线的距离;(2)、为了观看舒适,在(1)的情况下,把绕点逆时针旋转后,再将绕点顺时针旋转,使点落在直线上即可,求旋转的角度.