（人教版）2022-2023学年八年级数学下册20.1 数据的集中趋势 同步测试
试卷更新日期：2023-03-15 类型：同步测试
一、单选题
-
1. 在一次“爱心互助”捐款活动中，某班第一小组8名同学捐款的金额（单位：元）如下表：
金额/元
10
12
14
20
人数
2
3
2
1
这8名同学捐款的平均金额为（ ）
A、15元 B、14元 C、13.5元 D、13元2. 家乐福超市决定招聘广告策划人员一名，某应聘者三项素质测试的成绩如表：测试项目
创新能力
综合知识
语言表达
测试成绩（分数）
70
80
92
将创新能力、综合知识和语言表达三项测试成绩技5：3：2的比树计入总成绩，测该应聘者的总成绩是（ ）分．
A、77.4 B、80 C、92 D、以上都不对3. 从一组数据中取出a个x1 ， b个x2 ， c个x3 ， 组成一个样本，那么这个样本的平均数是（ ）A、 B、 C、 D、4. 某工厂共有50名员工，他们的月工资的平均数为m，现厂长决定给员工普加工资300元，则他们的新工资的平均数为（ ）A、m＋300 B、m C、m-300 D、无法确定5. 某商场销售A ， B ， C ， D四种商品，它们的单价依次是50元，30元，20元，10元．某天这四种商品销售数量的百分比如图所示，则这天销售的四种商品的平均单价是（ ）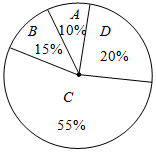
A、19.5元 B、21.5元 C、22.5元 D、27.5元6. 一组数据分别为3、5、8、4、7，这组数据的中位数为（ ）A、4 B、5 C、7 D、87. 某鞋店在一周内同一款不同尺码品牌鞋的销量情况如图所示，若尺码不同的每双鞋的利润相同，则下一周该鞋店应多进鞋的尺码是（ ）
A、22.5 B、23 C、23.5 D、248. 小明与小华本学期都参加了5次数学考试（总分均为100分），数学老师想判断这两位同学的数学成绩谁更稳定，在作统计分析时，老师需比较这两人5次数学成绩的（ ）A、平均数 B、方差 C、众数 D、中位数9. 某同学一周中每天体育运动所花时间（单位：分钟）分别为：35，39，45，40，55，48，45，这组数据的中位数是（ ）．A、35 B、40 C、45 D、5510. 根据疫情防控的要求，学校对所有进入校园的师生进行体温检测，其中7名学生的体温（单位）如下：36.6，36.7，36.6，36.4，36.6，36.5，36.7，这组数据的众数和中位数分别是（ ）A、36.6，36.4 B、36.6，36.6 C、36.7，36.4 D、36.7，36.6二、填空题
-
11. 在校园歌手大奖赛上，比赛规则是：七位评委打分，去掉一个最高分和一个最低分后，所剩数据取平均数即为选手的最后得分．七位评委给某位歌手打出的分数如下：9.5，9.4，9.6，9.9，9.3，9.7，9.0，则这位歌手的最后得分是 ．12. 小明参加演讲比赛，演讲内容、演讲能力、演讲效果三个方面得分分别为85分、95分、95分，按演讲内容占50％、演讲能力占40％、演讲效果占10％计算成绩，则小明的成绩是分．13. 如图是小明某一天测得的7次体温情况的折线统计图，这组数据的中位数是 ．
14. 已知一组数据3，6，9，a，5，7的唯一众数是6，那么这组数据的平均数是 ．15. 北京冬奥会金牌榜前十位的金牌数分别为16，12，9，8，8，8，7，7，6，5．这组数据的平均数、众数和中位数中，最大的是 ．三、解答题
-
16. 某养鱼个体经营户在鱼塘放养了5500条草鱼苗，鱼苗的成活率为90%．养殖一段时间后，想估计鱼塘中产量，随机网了三次，第一次网出30条鱼，平均每条鱼的重量是1kg；第二次网出了45条鱼，平均每条鱼的重量是1.3kg；第三次网出了35条鱼，平均每条鱼的重量是1.2kg，请你估计鱼塘中鱼的总重量是多少kg？17. 北京人大附中小强同学学完“数据分析”的相关知识后后，就回家帮助母亲预算家庭一年煤气开支，他连续7个月估计了每个月的家庭煤气使用数据，并记录如下表：
日期
11月1日
12月1日
1月1日
2月1日
3月1日
4月1日
5月1日
使用量(方)
9.41
9.59
9.74
9.93
10.13
10.13
11.07
①写出这7个月每月用煤气数的众数、中位数、平均数．
②若每方煤气需要支出2.2元，估计小强家一年的煤气费大约为多少元？
18. 某单位若干名职工参加“预防新冠肺炎”卫生知识竞赛，将成绩制成如图所示的扇形统计图和条形统计图，根据图中提供的信息，求这些职工成绩的中位数和平均数.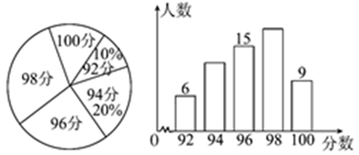
四、综合题
-
19. 从甲、乙两个企业随机抽取部分职工，对某个月收入情况进行调查，并把调查结果分别制成扇形统计图和条形统计图．
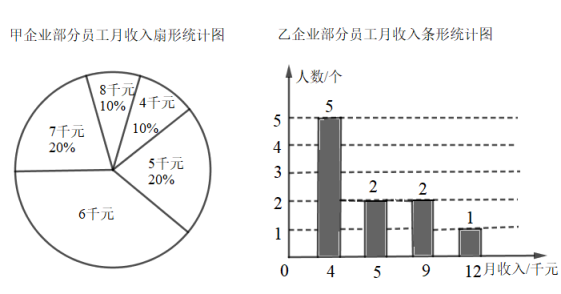(1)、在扇形统计图中，“6千元”所在的扇形的圆心角是；(2)、在调查人数中，比较甲企业的平均工资与乙企业的平均工资大小时，小明提出自己的看法：虽然不知道甲企业的调查人数，但是由加权平均数的定义，可以计算甲企业的平均工资，因此可以比较，小明的说法符合题意吗？若符合题意，请比较甲企业的平均工资与乙企业的平均工资大小．20. 某校举行八年级学生数学素养大赛，比赛共设四个项目：七巧板拼图、趣题巧解、数学应用、魔方复原，每个项目得分按一定百分比折算后记入总分．下表为甲、乙、丙三位同学得分情况（单位：分）七巧板拼图
趣题巧解
数学应用
魔方复原
甲
66
89
86
68
乙
66
60
80
68
丙
66
80
90
68
(1)、比赛后，甲猜测七巧板拼图、趣题巧解、数学应用、魔方复原这四个项目得分分别按10%，40%，20%，30%折算记入总分，根据猜测，求出甲的总分；(2)、本次大赛组委会最后决定，总分为80分以上（包括80分）的学生获一等奖，现获悉乙、丙的总分分别是70分、80分，甲的七巧板拼图、魔方复原两项得分折算后分数和是20分，问甲能否获得这次比赛的一等奖．21. 某校八年级全体同学参加了某项捐款活动，随机抽查了部分同学捐款的情况，并统计绘制成了如图两幅不完整的条形统计图和扇形统计图，请根据所提供的信息，解答下列问题：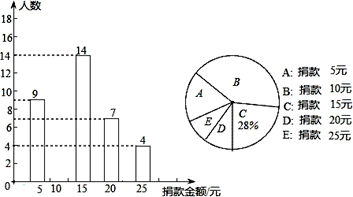
(1)、本次共抽查学生 ▲ 人，并将条形图补充完整；(2)、捐款金额的众数是 ， 中位数是；(3)、在八年级850名学生中，捐款20元及以上（含20元）的学生估计有多少人？22. 某校为了调查学生对环境保护知识的了解情况，从七、八两个年级各随机抽取50名学生进行了相关知识测试，获得了他们的成绩（百分制），并对数据（成绩）进行了整理、描述和分析，下面给出了部分信息：a．八年级50名学生成绩的频数分布统计表如下：
成绩x
学生人数
5
14
15
13
3
b．八年级成绩在这一组的是：
71 71 72 72 73 75 75 75 76 77 77 78 79 79 79
c．七、八两个年级成绩的平均分、中位数、众数和方差如下．
年级
平均数
中位数
方差
七
74
73.8
122.3
八
74
n
89.2
根据以上信息，回答下列问题：
(1)、表格中n＝ ．(2)、在此次测试中，某学生的成绩是74.5分，在他所属年级排在前20名，由表中数据可知该学生是年级的学生．（填“七”或“八”）(3)、根据以上信息，你认为七、八两个年级中，哪个年级学生了解环境保护知识的情况较好，请从两个方面说出你的判断依据．23. 某校为了调查学生平均每天的睡眠时间，在全校随机抽取了20名学生进行调查，并将收集到的学生平均每天睡眠时间t（小时）统计如下表：睡眠时间t（小时）
6
6.5
7
7.5
8
8.5
人数（人）
2
2
4
4
6
2
(1)、求这组数据的众数、平均数、中位数；(2)、请估计该校1500名学生平均每天睡眠时间超过8小时（含8小时）的人数．