（人教版）2022-2023学年八年级数学下册19.3 课题学习：选择方案 同步测试
试卷更新日期：2023-03-15 类型：同步测试
一、单选题
-
1. 小明同学在一次学科综合实践活动中发现，某品牌鞋子的长度y cm与鞋子的码数x之间满足一次函数关系，下表给出y与x的一些对应值：
码数x
26
30
34
42
长度y cm
18
20
22
26
根据小明的数据，可以得出该品牌38码鞋子的长度为（ ）
A、24cm B、25cm C、26cm D、38cm2. 在物理实验课上，小鹏利用滑轮组及相关器材进行实验，他把得到的拉力和所悬挂物体的重力的几组数据用电脑绘制成如下图象（不计绳重和摩擦），请你根据图象判断以下结论正确的序号有（ ）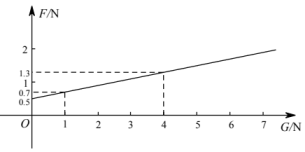
①物体的拉力随着重力的增加而增大；②当物体的重力N时，拉力N；③拉力F与重力G成正比例函数关系；④当滑轮组不悬挂物体时，所用拉力为0.5N．
A、①② B、②④ C、①④ D、③④3. 清明假期第一天天气晴朗，小明和爸爸去爬山．小明和爸爸同时从山脚出发，由于爸爸有爬山经验，匀速爬到山顶．小明刚开始的速度比爸爸快，累了之后减速继续爬山，和爸爸相遇后0.5h才加速追赶爸爸，最终爸爸用2h爬到了山顶，小明比爸爸晚了6min到达．他们出发的时间x（单位：h）与爬山的路程y（单位：km）的函数图象如图所示，则下列说法错误的是（ ）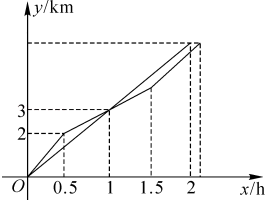
A、爸爸爬山的速度为3km/h B、1.5h时爸爸与小明的距离为0.5km C、山脚到山顶的总路程为6km D、小明加速追赶爸爸时的速度为3km/h4. 如图，欣欣妈妈在超市购买某种水果所付金额y（元）与购买x（千克）之间的函数图象如图所示，则一次性购买6千克这种水果比平均分2次购买可节省（ ）元．
A、4 B、3 C、2 D、15. 在一次 米的长跑比赛中，甲、乙两人所跑的路程S (米)与各自所用时间t(秒)之间的函数图象分别为线段 和折线 则下列说法正确的是（ ）
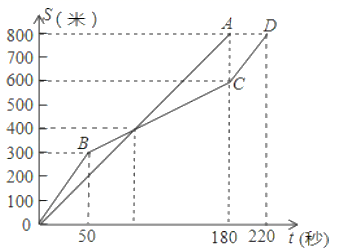A、甲的速度随时间的增加而增大 B、乙的平均速度比甲的平均速度大 C、在起跑后第 秒时，两人相遇 D、在起跑后第 秒时，乙在甲的前面6. 如图是甲、乙两个探测气球所在位置的海拔高度 （单位： ）关于上升时间 （单位： ）的函数图象.有下列结论：①当 时，两个探测气球位于同一高度
②当 时，乙气球位置高；
③当 时，甲气球位置高；
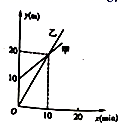
其中，正确结论的个数是（ ）
A、 个 B、 个 C、 个 D、 个7. 公式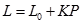
表示当重力为P时的物体作用在弹簧上时弹簧的长度. 
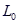表示弹簧的初始长度，用厘米（cm）表示，K表示单位重力物体作用在弹簧上时弹簧的长度，用厘米（cm）表示．下面给出的四个公式中，表明这是一个短而硬的弹簧的是（ ） A、L=10+0.5P B、L=10+5P C、L=80+0.5P D、L=80+5P8. 如图是甲、乙两个探测气球所在位置的海拔高度y（单位：m）关于上升时间x（单位： ）的函数图象.有下列结论：①当 时，两个探测气球位于同一高度
②当 时，乙气球位置高；
③当 时，甲气球位置高；
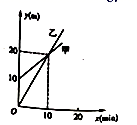
其中，符合题意结论的个数是（ ）
A、 个 B、 个 C、 个 D、 个9. 如图，购买一种苹果，所付款金额y（元）与购买量x（千克）之间的函数图象由线段OA和射线AB组成，则一次购买5千克这种苹果比分五次购买1千克这种苹果可节省（ ）元.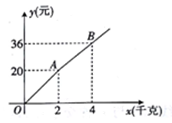
A、4 B、5 C、6 D、710. 如果弹簧的长度ycm与所挂物体的质量x(kg)的关系是一次函数，图象如图所示，那么弹簧不挂物体时的长度是（ ）
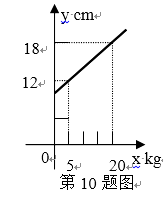A、9cm B、10cm C、10.5cm D、11cm二、填空题
-
11. 弹簧的长度（cm）与所挂物体的质量（kg）之间的关系如图所示，那么弹簧不挂物体时的长度是cm．
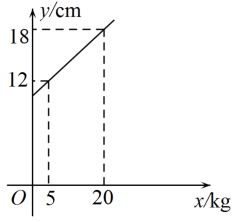12. 某苹果种植合作社通过网络销售苹果，如图所示的线段AB反映了苹果的日销售量y（千克）与销售单价x（元/千克）间的函数关系，已知1千克苹果的成本是5元，如果某天该合作社的苹果销售单价为8元/千克，那么这天销售苹果的盈利是 元．
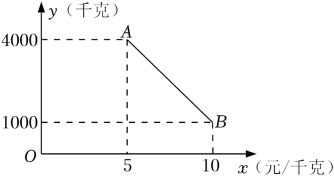13. 小明租用共享单车从家出发，匀速骑行到相距2400米的图书馆还书．小明出发的同时，他的爸爸以每分钟96米的速度从图书馆沿同一条道路步行回家，小明在图书馆停留了3分钟后沿原路按原速骑车返回．设他们出发后经过t（分）时，小明与家之间的距离为 （米），小明爸爸与家之间的距离为 （米），图中折线OABD、线段EF分别表示 、 与t之间的函数关系的图象．小明从家出发，经过分钟在返回途中追上爸爸．
14. 从A地向B地打长途电话，按时收费，3分钟内收费2.4元，以后每超过1分钟加收1元，若通话t分钟（t≥3），则需付电话费y（元）与t（分钟）之间的函数关系式是。15. 某鲜花销售商经过市场调查，发现有甲、乙、丙、丁四种鲜花组合比较受顾客的喜欢，于是制定了进货方案，其中甲、丙的进货量相同，乙、丁的进货量相同，甲与丁的单价相同，甲、乙与丙、丁的单价和均为66元/束，且甲、乙的进货总价比丙、丁的进货总价多600元.由于年末资金周转紧张，所以临时决定只购进甲、乙两种组合，甲、乙的进货量与原方案相同，且进货总数不超过500束，则该销售商最多需要准备元进货资金.
三、解答题
-
16. 一辆轿车在高速公路上匀速行使，油箱存油量Q（升）与行使的路程S（km）成一次函数关系.若行使100km时，油箱存油43.5升，当行使300km时，油箱存油30.5升，请求出这个一次函数关系式，并写出自变量S的取值范围.17. 为了预防新冠肺炎，某药店欲购进甲、乙两种防护口罩进行销售，有关信息如表：
进价（元/袋）
售价（元/袋）
甲种防护口罩
20
25
乙种防护口罩
30
37
该药店准备购进甲、乙两种防护口罩共40袋，且甲种防护口罩不少于30袋，问应该怎样进货，才能使总获利最大，最大利润为多少元？
18. 每年6月5日是“世界环境日”，某小区为积极响应“共建清洁美丽世界”的号召，计划购进A，B两种树苗共60棵美化小区环境，已知A种树苗每棵130元，B种树苗每棵150元，若购进A种树苗的数量不多于B种树苗的两倍，则A，B两种树苗各购进多少棵时，费用最省？最省费用是多少？四、综合题
-
19. 抗击疫情，我们在行动．某药店销售A型和B型两种型号的口罩，销售一箱A型口罩可获利100元，销售一箱B型口罩可获利120元．该药店计划一次购进两种型号的口罩共80箱，其中B型口罩的进货量不超过A型口罩的3倍．设购进A型口罩x箱，这80箱口罩的销售总利润为y元．(1)、求y与x的函数关系式；(2)、该商店购进A型、B型口罩各多少箱，才能使销售利润最大？最大利润是多少？20. 某零售店销售甲、乙两种蔬菜，甲种蔬菜每千克获利1.1元，乙种蔬菜每千克获利1.5元，该店计划一次购进这两种蔬菜共56千克，并能全部售出．设该店购进甲种蔬菜x千克，销售这56千克蔬菜获得的总利润为y元．(1)、求y与x的关系式；(2)、若乙种蔬菜的进货量不超过甲种蔬菜的 ， 则该店购进甲、乙两种蔬菜各多少千克时，获得的总利润最大？最大总利润是多少？21. 某家具商场计划购进某种餐桌、餐椅进行销售，有关信息如下表：
原进价（元/张）
零售价（元/张）
成套售价（元/套）
餐桌
a
270
500
餐椅
a－110
70
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同．
(1)、上表中a的值为；(2)、若该商场购进餐椅的数量是餐桌数量的5倍还多20张，且餐桌和餐椅的总数量不超过200张．该商场计划将一半的餐桌成套（一张餐桌和四张餐椅配成一套）销售，其余餐桌、餐椅以零售方式销售．请问怎样进货，才能获得最大利润？最大利润是多少？22. 疫情期间，某乳品公司计划向马关县红十字会捐赠一批牛奶，甲运输公司提出：每千克运费0.48元，不收取其他费用：乙运输公司提出：每千克运费0.28元，另收取其他费用600元．(1)、设这批牛奶共x千克，选择甲公司运输，所需费用为元，选择乙公司运输，所需费用为元，请分别写出 ， 与x之间的关系式；(2)、该公司选择哪家运输公司运送这批牛奶更划算，请说明理由．23. 某商场计划购进一批篮球和足球，其中篮球的单价比足球多30元．已知用360元购进的足球和用480元购进的篮球数量相等．(1)、问篮球和足球的单价各是多少元？(2)、若篮球的售价为150元，足球的售价为110元，商场计划用不超过10350元购进两种球共100个，其中篮球不少于40个，问商场共有几种购货方案？哪种方案商场获利最大，并求出最大利润？