(人教版)2022-2023学年八年级数学下册19.1 变量与函数 同步测试
试卷更新日期:2023-03-15 类型:同步测试
一、单选题
-
1. 一本笔记本5元,买x本共付y元,则变量是( )A、5 B、5和x C、x D、x和y2. 一个圆形花坛,面积S与半径的函数关系式中关于常量和变量的表述正确的是( )A、常量是2,变量是、、 B、常量是2、 , 变量是、 C、常量是2,变量是、 D、常量是 , 变量是、3. 下列曲线中,不表示是的函数图象的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图①,在平面直角坐标系中,矩形ABCD在第一象限,且AB∥y轴.直线M: y=﹣x沿x轴正方向平移,被矩形ABCD截得的线段EF的长度l与平移的距离a之间的函数图象如图②,那么矩形ABCD的面积为( )
4. 如图①,在平面直角坐标系中,矩形ABCD在第一象限,且AB∥y轴.直线M: y=﹣x沿x轴正方向平移,被矩形ABCD截得的线段EF的长度l与平移的距离a之间的函数图象如图②,那么矩形ABCD的面积为( ) A、10 B、12 C、15 D、185. 如图表示的是嘉淇父母外出散步时,离家的距离与时间的函数关系.(图代表嘉淇的母亲,图代表嘉淇的父亲)
A、10 B、12 C、15 D、185. 如图表示的是嘉淇父母外出散步时,离家的距离与时间的函数关系.(图代表嘉淇的母亲,图代表嘉淇的父亲)①嘉淇的父母出去散步,从家走了20分钟到一个离家900米的报亭;②母亲随即按原来的速度返回;③父亲在报亭看报10分钟;④然后父亲用15分钟返回家.
以上描述,符合函数图象的是( )
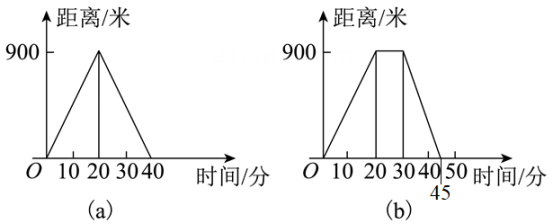 A、①③ B、②④ C、①②③ D、①②③④6. 某地出租车计费方式如下:3km以内只收起步价5元,超过3km的除收起步价外,每超出1km另加收1元;不足1km的按1km计费.则能反映该地出租车行驶路程 (km)与所收费用 (元)之间的函数关系的图象是( )A、
A、①③ B、②④ C、①②③ D、①②③④6. 某地出租车计费方式如下:3km以内只收起步价5元,超过3km的除收起步价外,每超出1km另加收1元;不足1km的按1km计费.则能反映该地出租车行驶路程 (km)与所收费用 (元)之间的函数关系的图象是( )A、 B、
B、 C、
C、 D、
D、 7. 函数中自变量的取值范围( )A、 B、 C、 D、8. 函数自变量x的取值范围是( )A、 B、 C、 D、9. 如图是某蓄水池的横断面的示意图,分深水区和浅水区,如果向这个蓄水池中以固定的水流量(单位时间注水的体积)注水(注满水后停止注水),那么下列图中能大致表示水的深度 h 与注水时间 t 之间关系的图象的是( )
7. 函数中自变量的取值范围( )A、 B、 C、 D、8. 函数自变量x的取值范围是( )A、 B、 C、 D、9. 如图是某蓄水池的横断面的示意图,分深水区和浅水区,如果向这个蓄水池中以固定的水流量(单位时间注水的体积)注水(注满水后停止注水),那么下列图中能大致表示水的深度 h 与注水时间 t 之间关系的图象的是( )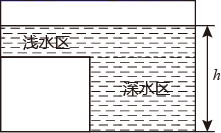 A、
A、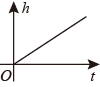 B、
B、 C、
C、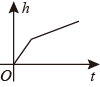 D、
D、 10. 图(1)是饮水机的图片.打开出水口,饮水桶中水面由图(1)下降到图(3)的位置的过程中,如果水减少的体积是y,水面下降的高度是x,那么能够表示y与x之间函数关系的图象可能是( )
10. 图(1)是饮水机的图片.打开出水口,饮水桶中水面由图(1)下降到图(3)的位置的过程中,如果水减少的体积是y,水面下降的高度是x,那么能够表示y与x之间函数关系的图象可能是( ) A、
A、 B、
B、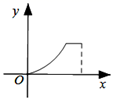 C、
C、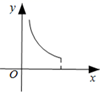 D、
D、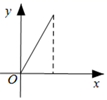
二、填空题
-
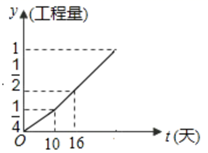
11. 如图,甲,乙两个工程队完成某项工程,首先是甲单独做了 天,然后乙队加入合做,完成剩下的全部工程.设工程总量为单位 ,工程进度满足如图所示的函数关系,设 甲的工作效率:乙的工作效率,则 的值为.
 12. 星期六下午,小张和小王同时从学校沿相同的路线去书店买书,小王出发4分钟后发现忘记带钱包,立即调头按原速原路回学校拿钱包,小王拿到钱包后,以比原速提高20%的速度按原路赶去书店,结果还是比小张晚4分钟到书店(小王拿钱包的时间忽略不计).在整个过程中,小张保持匀速运动,小王提速前后也分别保持匀速运动,如图所示是小张与小王之间的距离y(米)与小王出发的时间x(分钟)之间的函数图象,则学校到书店的距离为米.
12. 星期六下午,小张和小王同时从学校沿相同的路线去书店买书,小王出发4分钟后发现忘记带钱包,立即调头按原速原路回学校拿钱包,小王拿到钱包后,以比原速提高20%的速度按原路赶去书店,结果还是比小张晚4分钟到书店(小王拿钱包的时间忽略不计).在整个过程中,小张保持匀速运动,小王提速前后也分别保持匀速运动,如图所示是小张与小王之间的距离y(米)与小王出发的时间x(分钟)之间的函数图象,则学校到书店的距离为米.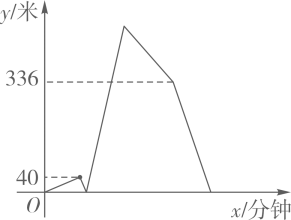 13. 如图,一个函数的图象由射线 ,线段 ,射线 组成,其中点 , , , .当y随x的增大而增大时,则x的取值范围是 .
13. 如图,一个函数的图象由射线 ,线段 ,射线 组成,其中点 , , , .当y随x的增大而增大时,则x的取值范围是 .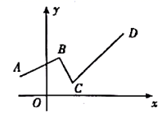 14. 如图,△ABC中,AB=AC,CD⊥AB于D,BD=1,设BC=x,AD=y,当x>时,y关于x的函数解析式为 .
14. 如图,△ABC中,AB=AC,CD⊥AB于D,BD=1,设BC=x,AD=y,当x>时,y关于x的函数解析式为 . 15. 当时,函数的值是 .
15. 当时,函数的值是 .三、解答题
-
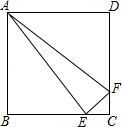
16. 座钟的摆针摆动一个来回所需的时间称为一个周期,其计算公式为 , 其中T表示周期(单位s),l表示摆长(单位),π取3,.假如一台座钟的摆长为0.2.它每摆动一个来回发出一次滴答声,那么在1分钟内,该座钟大约发出了多少次滴答声?17. 如图,正方形ABCD的边长为4cm,E,F分别是BC,CD边上一动点,点E,F同时从点C出发,以每秒2cm的速度分别向点B,D运动,当点E与点B重合时,运动停止,设运动时间为x(s),运动过程中△AEF的面积为y(cm2),求y关于x的函数表达式,并写出自变量x的取值范围.
 18. 一次越野跑中,当李明跑了1600米时,小刚跑了1450米,此后两人匀速跑的路程s(米)与时间t(秒)的关系如图,结合图象解答下列问题:Ⅰ.请你根据图象写出二条信息;Ⅱ.求图中S1和S0的位置.
18. 一次越野跑中,当李明跑了1600米时,小刚跑了1450米,此后两人匀速跑的路程s(米)与时间t(秒)的关系如图,结合图象解答下列问题:Ⅰ.请你根据图象写出二条信息;Ⅱ.求图中S1和S0的位置.
四、综合题
-
19. 如图,长为32米,宽为20米的长方形地面上,修筑宽度均为m米的两条互相垂直的小路(图中阴影部分),其余部分作耕地,如果将两条小路铺上地砖,选用地砖的价格是60元/米2 .
 (1)、写出买地砖需要的钱数y(元)与m(米)的函数关系式 .(2)、计算当m=3时,地砖的费用.20. 如图所示,在一个边长为12cm的正方形的四个角都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
(1)、写出买地砖需要的钱数y(元)与m(米)的函数关系式 .(2)、计算当m=3时,地砖的费用.20. 如图所示,在一个边长为12cm的正方形的四个角都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.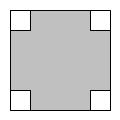 (1)、在这个变化过程中,自变量、因变量各是什么?(2)、如果小正方形的边长为xcm,图中阴影部分的面积为ycm , 请写出y与x的关系式;(3)、当小正方形的边长由1cm变化到5cm时,阴影部分的面积是怎样变化的?21. 小文家与文具店相距960m,小文从家出发,沿笔直的公路匀速步行12min来到文具店买笔记本,停留3min,因家中有事,便沿原路匀速跑步以160m/min返回家中.
(1)、在这个变化过程中,自变量、因变量各是什么?(2)、如果小正方形的边长为xcm,图中阴影部分的面积为ycm , 请写出y与x的关系式;(3)、当小正方形的边长由1cm变化到5cm时,阴影部分的面积是怎样变化的?21. 小文家与文具店相距960m,小文从家出发,沿笔直的公路匀速步行12min来到文具店买笔记本,停留3min,因家中有事,便沿原路匀速跑步以160m/min返回家中. (1)、小文返回家的速度比去文具店的速度快 m/min;(2)、画出整个过程中,小文离家的距离y(m)与时间(min)的函数图象;(3)、根据图象回答:小文从家出发后多少分钟离家的距离为480m?22. 已知函数 ( 为常数).(1)、当 时,
(1)、小文返回家的速度比去文具店的速度快 m/min;(2)、画出整个过程中,小文离家的距离y(m)与时间(min)的函数图象;(3)、根据图象回答:小文从家出发后多少分钟离家的距离为480m?22. 已知函数 ( 为常数).(1)、当 时,①点 在此函数图象上,求 的值;
②求此函数的最大值;
(2)、已知线段 的两个端点坐标分别为 、 ,当此函数的图象与线段 只有一个交点时,求 的取值范围.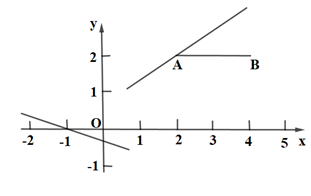
 23. 研究发现,学生对概念的接受能力y与提出概念所用的时间x(分钟)之间有如下关系:
23. 研究发现,学生对概念的接受能力y与提出概念所用的时间x(分钟)之间有如下关系:提出概念所用的时间x(分钟)
对概念的接受能力y
根据以上信息,回答下列问题:
(1)、当提出概念所用的时间为 分钟时,学生的接受能力约是多少?(2)、当提出概念所用的时间为多少分钟时,学生的接受能力最强?(3)、当 时,学生的接受能力随提出概念的时间增加而怎么样发生变化?当 时,学生的接受能力随提出概念的时间增加而怎么样发生变化?