备战2023年中考数学细点逐一突破真题训练第13章图形的相似
试卷更新日期:2023-03-15 类型:二轮复习
一、相似型
-
1. 如图,将图形用放大镜放大,应该属于( ).
 A、平移变换 B、相似变换 C、旋转变换 D、对称变换2. 将等边三角形,菱形,矩形,正方形各边向外平移1个单位并适当延长,得到如图所示的4组图形,变化前后的两个多边形一定相似的有( )
A、平移变换 B、相似变换 C、旋转变换 D、对称变换2. 将等边三角形,菱形,矩形,正方形各边向外平移1个单位并适当延长,得到如图所示的4组图形,变化前后的两个多边形一定相似的有( ) A、1组 B、2组 C、3组 D、4组3. 一块矩形绸布的长AB=a米,宽AD=1米,按照图中所示的方式将它裁成完全相同的三面矩形彩旗,且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,那么a的值为( )
A、1组 B、2组 C、3组 D、4组3. 一块矩形绸布的长AB=a米,宽AD=1米,按照图中所示的方式将它裁成完全相同的三面矩形彩旗,且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,那么a的值为( ) A、3 B、 C、3 D、
A、3 B、 C、3 D、二、平行线平分线段成比例
-
4. 下列四组线段中,不成比例的是( )A、3,9,2,6 B、1, , , C、1,2,4,8 D、1,2,3,95. 点把 分割成 和 两段,如果 是 和 的比例中项,那么下列式子成立的是( )A、 B、 C、 D、6. 如图,在中,分别是、上的点, , 与相交于 , 则下列结论一定正确的是( )
 A、 B、 C、 D、7. 如图, , 直线与 , , 分别交于点和点 , 若 , , 则DE的长是( )
A、 B、 C、 D、7. 如图, , 直线与 , , 分别交于点和点 , 若 , , 则DE的长是( ) A、8 B、6 C、4 D、108. 如图,E是△ABC的中线AD上一点,CE的延长线交AB于点F,若AF=2,ED=3AE,则AB的长为 .
A、8 B、6 C、4 D、108. 如图,E是△ABC的中线AD上一点,CE的延长线交AB于点F,若AF=2,ED=3AE,则AB的长为 . 9. 如图,正方形的对角线交于点O,的平分线交于G,交于F,求证:.
9. 如图,正方形的对角线交于点O,的平分线交于G,交于F,求证:.
三、相似三角形判定
-
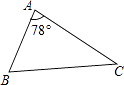
10. 如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
 A、
A、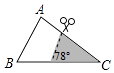 B、
B、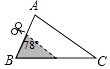 C、
C、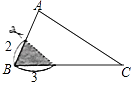 D、
D、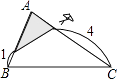 11. 如图,已知 , 那么添加下列一个条件后,仍无法判定的是( )
11. 如图,已知 , 那么添加下列一个条件后,仍无法判定的是( )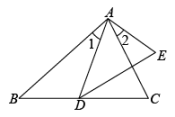 A、 B、 C、 D、12. 已知:、是的边、上的点, , , , , 求证:.
A、 B、 C、 D、12. 已知:、是的边、上的点, , , , , 求证:. 13. 以下各图均是由边长为1的小正方形组成的网格, 均在格点上.
13. 以下各图均是由边长为1的小正方形组成的网格, 均在格点上.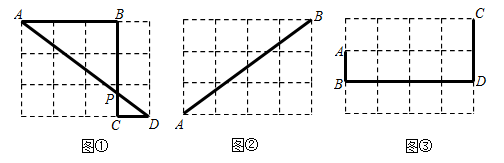 (1)、在图①中,的值为;(2)、利用网格和无刻度的直尺作图,保留痕迹,不写作法.
(1)、在图①中,的值为;(2)、利用网格和无刻度的直尺作图,保留痕迹,不写作法.①如图②,在上找一点 , 使;
②如图③,在上找一点 , 使 .
14. 下列图形中,与如图所示的 ABC相似的是( )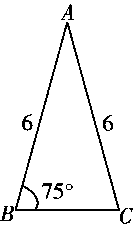 A、
A、 B、
B、 C、
C、 D、
D、 15. 如图,等边三角形△ACB的边长为3,点P为BC上的一点,点D为AC上的一点,连接AP、PD,∠APD=60°.
15. 如图,等边三角形△ACB的边长为3,点P为BC上的一点,点D为AC上的一点,连接AP、PD,∠APD=60°. (1)、求证:△ABP∽△PCD;(2)、若PC=2,求CD的长.16. 如图,中,是直角,过斜边中点M而垂直于斜边的直线交的延长线于E,交于D,连接.
(1)、求证:△ABP∽△PCD;(2)、若PC=2,求CD的长.16. 如图,中,是直角,过斜边中点M而垂直于斜边的直线交的延长线于E,交于D,连接.
求证:
(1)、;(2)、.四、相似三角形的相关证明计算
-
17. 已知,如图, = = ,那么△ABD与△BCE相似吗?为什么?
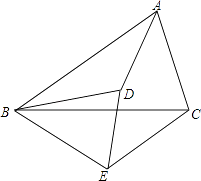 18. 如图,是等边三角形,D、E在BC所在的直线上,且 . 求证: .
18. 如图,是等边三角形,D、E在BC所在的直线上,且 . 求证: . 19. 在△ABC中.∠C=90°,点D,E分别在BC边和AC边上,AD,BE相交于点F.
19. 在△ABC中.∠C=90°,点D,E分别在BC边和AC边上,AD,BE相交于点F. (1)、图1,若∠AEF=∠BDF,求证:;(2)、如图2.若D为BC的中点,AE=EF.求证:AC=BF;(3)、如图3.若AE=CD,BD=AC.求∠AFE的度数.20. 如图,四边形ABCD内接于⊙O,对角线AC,BD交于点E.
(1)、图1,若∠AEF=∠BDF,求证:;(2)、如图2.若D为BC的中点,AE=EF.求证:AC=BF;(3)、如图3.若AE=CD,BD=AC.求∠AFE的度数.20. 如图,四边形ABCD内接于⊙O,对角线AC,BD交于点E. (1)、求证:△AED∽△BEC;(2)、若BD平分∠ABC,求证:CD2=DE•DB;(3)、在(2)小题的条件下,若DE=4,BE=2,过圆心O点,作OF⊥CD于点F,OF=2,求该圆的半径长.21. 已知:如图,在中,平分交于D.
(1)、求证:△AED∽△BEC;(2)、若BD平分∠ABC,求证:CD2=DE•DB;(3)、在(2)小题的条件下,若DE=4,BE=2,过圆心O点,作OF⊥CD于点F,OF=2,求该圆的半径长.21. 已知:如图,在中,平分交于D. (1)、求证:;(2)、延长至点E,联结、 , 如果 , 求证: .22. 如图,已知中, , , 点D、E在边上,.
(1)、求证:;(2)、延长至点E,联结、 , 如果 , 求证: .22. 如图,已知中, , , 点D、E在边上,.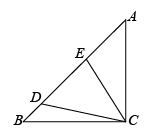 (1)、求证:;(2)、当 , 时,求的长.
(1)、求证:;(2)、当 , 时,求的长.五、相似三角形实际应用
-
23. 数学课外活动小组的同学们,带着皮尺去测量某河道因挖沙形成的“圆锥形坑”的深度(如图),点为沙坑底面所在圆的圆心,为其顶点,甲同学直立于沙坑坑沿的圆周所在的平面上,当他位于时,其视线恰好经过沙坑坑沿圆周上一点看到坑底(甲同学的视线起点与点 , 点三点共线),为了求得圆锥形坑的深度(圆锥的高),该同学列出了如下表达式,其中错误的是( )
 A、 B、 C、 D、24. 雨过天晴,小李急忙跑到室外呼吸新鲜空气,广场上E处有一处积水,如图,若小李站在D处距积水2米,他正好从水面上看到距他约10米的前方一棵树的顶端A的影子.已知点D、E、B在同一直线上,AB⊥BD,CD⊥BD,小李的眼睛到地面的距离CD为1.6米,求树AB的高.(∠CED=∠AEB,积水水面大小忽略不计)
A、 B、 C、 D、24. 雨过天晴,小李急忙跑到室外呼吸新鲜空气,广场上E处有一处积水,如图,若小李站在D处距积水2米,他正好从水面上看到距他约10米的前方一棵树的顶端A的影子.已知点D、E、B在同一直线上,AB⊥BD,CD⊥BD,小李的眼睛到地面的距离CD为1.6米,求树AB的高.(∠CED=∠AEB,积水水面大小忽略不计) 25. 如图1所示的是古代一种可以远程攻击的投石车,图2是投石车投石过程中某时刻的示意图,GP是杠杆,弹袋挂在点G,重锤挂在点P,点A为支点,点D是水平底板BC上的一点,AD=AC=3米,CD=3.6米.
25. 如图1所示的是古代一种可以远程攻击的投石车,图2是投石车投石过程中某时刻的示意图,GP是杠杆,弹袋挂在点G,重锤挂在点P,点A为支点,点D是水平底板BC上的一点,AD=AC=3米,CD=3.6米.
 (1)、投石车准备时,点G恰好与点B重合,此时AG和AC垂直,则AG=米.(2)、投石车投石瞬间,AP的延长线交线段DC于点E,若 ,则点G的上升高度为米.26. 矩形ABCD中,点P在对角线BD上(点P不与点B重合),连接AP,过点P作PE⊥AP交直线BC于点E.
(1)、投石车准备时,点G恰好与点B重合,此时AG和AC垂直,则AG=米.(2)、投石车投石瞬间,AP的延长线交线段DC于点E,若 ,则点G的上升高度为米.26. 矩形ABCD中,点P在对角线BD上(点P不与点B重合),连接AP,过点P作PE⊥AP交直线BC于点E. (1)、如图1,当AB=BC时,猜想线段PA和PE的数量关系:;(2)、如图2,当AB≠BC时.求证:(3)、若AB=8,BC=10,以AP,PE为边作矩形APEF,连接BF,当PE= 时,直接写出线段BF的长.27. 如图,在 中, ,正方形 的顶点 分别在边 、 上, 在边 上.
(1)、如图1,当AB=BC时,猜想线段PA和PE的数量关系:;(2)、如图2,当AB≠BC时.求证:(3)、若AB=8,BC=10,以AP,PE为边作矩形APEF,连接BF,当PE= 时,直接写出线段BF的长.27. 如图,在 中, ,正方形 的顶点 分别在边 、 上, 在边 上.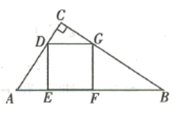 (1)、点 到 的距离为.(2)、求 的长.
(1)、点 到 的距离为.(2)、求 的长.