江西省吉安市2023届高三上学期1月期末质量检测数学（理）试题

试卷更新日期：2023-03-15 类型：期末考试

进入出卷网下载

一、单选题

1. 设集合 $A = {1 ， 3 ， 5 ， 7}$ ， $B = {x | | x - 2 | < 3}$ ，则（）

A、 $5 \in A \cap B$ B、 $5 \subseteq A \cup B$ C、 $A ⊆ B$ D、 ${7} \subseteq A \cup B$

查看试题解析
2. 已知 $z (1 - 2 i) = \bar{z} + 2$ ，则 $z =$ （）

A、 $1 + i$ B、 $1 - i$ C、 $- 1 + i$ D、 $- 1 - i$

查看试题解析
3. 在 $△ A B C$ 中， $\vec{A D} = λ \vec{D B}$ ， $E$ 为 $C D$ 的中点， $\vec{A E} = - \frac{5}{6} \vec{C A} + \frac{1}{3} \vec{C B}$ ，则 $λ =$ （）

A、2 B、1 C、 $\frac{1}{2}$ D、 $\frac{1}{3}$

查看试题解析
4. 某城市有一个面积为 $1 k m^{2}$ 的矩形广场，该广场为黄金矩形（它的宽与长的比为 $\frac{\sqrt{5} - 1}{2}$ ），现在在中央设计一个矩形草坪，四周是等宽的步行道，能否设计恰当的步行道的宽度使矩形草坪为黄金矩形？则下列选项正确的是（）

A、步行道的宽度 $10 m$ B、步行道的宽度 $20 m$ C、步行道的宽度 $30 m$ D、草坪不可能为黄金矩形

查看试题解析
5. 若 $x$ ， $y$ 满足约束条件 ${\begin{array}{l} x + y - 1 \geq 0 \\ x - y + 1 \geq 0 \\ 2 x - y - 2 \leq 0 \end{array}$ ，则 $z = {(x - 4)}^{2} + {(y - 1)}^{2}$ 的取值范围是（）

A、 $[10 ， 25]$ B、 $[5 ， 16]$ C、 $[\sqrt{10} ， 4]$ D、 $[\sqrt{5} ， 4]$

查看试题解析
6. 一个几何体的三视图如图所示，其中正视图和俯视图是直角边长分别为2和4的两个全等的直角三角形.则这个几何体的外接球的体积为（）

A、 $4 \sqrt{3} π$ B、 $8 \sqrt{6} π$ C、 $\frac{16}{3} \sqrt{2} π$ D、 $32 \sqrt{3} π$

查看试题解析
7. 已知点 $A (- 1 ， - 2)$ ， $B (0 ， a)$ ，若直线 $A B$ 关于 $y = a$ 的对称直线 $l$ 与圆 $C$ ： ${(x - 3)}^{2} + y^{2} = 18$ 交于 $M$ ， $N$ 两点，则 $| M N |$ 的最小值为（）

A、 $2 \sqrt{2}$ B、 $3 \sqrt{2}$ C、 $2 \sqrt{10}$ D、 $4 \sqrt{2}$

查看试题解析
8. 中国共产党第二十次全国代表大会于2022年10月16日在北京召开，10月17日各代表团分组讨论党的二十大报告．某媒体5名记者到甲、乙、丙3个小组进行宣传报道，每名记者只去1个小组，每个小组最多两名记者，若记者 $A$ 不去甲组，则不同的安排方法共有（）

A、15种 B、30种 C、60种 D、90种

查看试题解析
9. 记 $△ A B C$ 的内角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，已知 $2 b s i n B = (2 c + a) s i n C + (2 a + c) \cdot s i n A$ .则 $s i n A + s i n C$ 的最大值为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、1 D、2

查看试题解析
10. 已知实数 $x$ ， $y$ 满足 $x > 0$ ， $y > 0$ ，且 $x + \frac{y}{2} + \frac{1}{x} + \frac{2}{y} = 5$ ，则 $2 x + y$ 的最大值为（）

A、10 B、8 C、4 D、2

查看试题解析
11. 已知函数 $f (x)$ 及其导函数 $f^{'} (x)$ 的定义域均为R都为连续函数，记 $g (x) = f^{'} (x)$ ，若 $f (1 - x)$ ， $g (x)$ 均为奇函数，设 $A (x_{1} ， f (x_{1}))$ ， $B (x_{2} ， f (x_{2}))$ 为 $f (x)$ 图象上的不同两点. $C (x_{3} ， g (x_{3}))$ ， $D (x_{4} ， g (x_{4}))$ 为 $g (x)$ 图象上的不同两点，其中 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， $x_{4} \in (3 ， 7)$ ，且 $g (x)$ 在 $(5 ， 7)$ 上单调，若 $x_{1} + x_{2} = 10$ ， $g (x_{3}) = g (x_{4})$ ，则 $f (x_{1}) + f (x_{2}) + x_{3} + x_{4} =$ （）

A、0 B、5 C、10 D、20

查看试题解析
12. 椭圆 $C$ 的两个焦点为 $F_{1}$ ， $F_{2}$ ，以 $C$ 的短轴为直径的圆记为 $O$ ，过 $F_{1}$ 作圆 $O$ 的切线与 $C$ 交于 $M$ ， $N$ 两点，且 $c o s ∠ F_{1} N F_{2} = - \frac{3}{5}$ ，则 $C$ 的离心率为（）

A、 $\frac{\sqrt{5}}{3}$ B、 $\frac{2}{3}$ C、 $\frac{4}{5}$ D、 $\frac{\sqrt{65}}{9}$

查看试题解析

二、填空题

13. 某校第一次模拟考试的数学成绩 $X$ 近似地服从正态分布 $N (90 ， σ^{2})$ ，若 $P (X < 100) = 0.92$ ，则 $P (80 < X < 100) =$ .

查看试题解析
14. 记函数 $f (x) = c o s (ω x + \frac{π}{3})$ （ $ω > 0$ ）的最小正周期为 $T$ ，且 $y = f (x)$ 的图象关于 $x = \frac{π}{6}$ 对称，当 $ω$ 取最小值时， $f (\frac{T}{2}) =$ .

查看试题解析
15. 过抛物线 $C$ ： $y = 2 x^{2}$ 准线上的点 $P$ 作 $C$ 的两条切线，切点分别为 $A$ ， $B$ ，则 $k_{P A} \cdot k_{P B} =$ .

查看试题解析
16. 已知函数 $f (x) = | e^{x} - 1 |$ ， $x_{1} \leq 0 \leq x_{2} \leq 2$ ，函数 $f (x)$ 的图象在点 $A (x_{1} ， f (x_{1}))$ 和点 $B (x_{2} ， f (x_{2}))$ 处的两条切线互相垂直，且分別交 $y$ 轴于 $M$ ， $N$ 两点，则 $| M N |$ 的取值范围是.

查看试题解析

三、解答题

17. 设等差数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ， $a_{2} = 1$ ，数列 $b_{n}$ 为等比数列，其中 $b_{1} = a_{2}$ ， $b_{2} = a_{3}$ ， $b_{3} = a_{6}$ .

(1)、求 ${a_{n}}$ ， ${b_{n}}$ 的通项公式；

(2)、若 $b_{3} \neq a_{3}$ ，求 ${\frac{S_{n}}{n} + b_{n}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
18. 如图，在四棱锥 $P - A B C D$ 中， $A B ∥ C D$ ， $A D = C D = B C = P A = P C = \frac{1}{2} A B$ ， $B C ⊥ P A$ .

(1)、证明：平面 $P B C ⊥$ 平面 $P A C$ ；

(2)、若 $P B = 2 \sqrt{2}$ ，求点 $B$ 到平面 $P A D$ 的距离.

查看试题解析
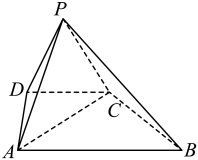19. 为了调查抖音平台某直播间带货服务的满意程度，现随机调查了年龄在20岁至70岁的100人，他们年龄的频数分布和“满意”的人数如下表：
年龄/岁
$[20 ， 30)$
$[30 ， 40)$
$[40 ， 50)$
$[50 ， 60)$
$[60 ， 70]$
频数
15
25
30
20
10
满意
13
20
27
16
4

(1)、根据上述统计数据填下面的 $2 \times 2$ 列联表，并判断是否有95%的把握认为年龄低于50岁的人和年龄不低于50岁的人对服务态度有差异；

年龄低于50岁的人数
年龄不低于50岁的人数
合计
满意
不满意
合计

(2)、若以频率估计概率，以100人的样本数据来估计全国玩抖音的市民（假设年龄均在20岁至70岁）的总体数据，若从在全国范围内任选5人，记 $X$ 表示抽到“满意”的人数，求 $X$ 的分布列与数学期望.
附： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ .
$P (K^{2} \geq k_{0})$
0.10
0.05
0.01
0.001
$k_{0}$
2.706
3.841
6.635
10.828

查看试题解析
20. 已知双曲线 $C$ ： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ （ $a > 0$ ， $b > 0$ ）与双曲线 $\frac{x^{2}}{2} - y^{2} = 1$ 的渐近线相同，点 $A (2 \sqrt{2} ， 1)$ 在 $C$ 上， $F_{2}$ 为 $C$ 的右焦点．

(1)、求 $C$ 的方程；

(2)、已知 $M$ 是直线 $l$ ： $x = t$ 上的任意一点，是否存在这样的直线 $l$ ，使得过点 $M$ 的直线与 $C$ 相切于点 $N$ ，且以 $M N$ 为直径的圆过点 $F_{2}$ ？若存在，求出直线 $l$ 的方程，若不存在，说明理由．

查看试题解析
21. 已知函数 $f (x) = 3 a l n x - (a - 3) x$ ， $a \in R$ .

(1)、当 $a = 1$ 时，求曲线 $g (x) = f (x) - 3 l n x - s i n x$ 在 $x = \frac{π}{2}$ 处的切线方程；

(2)、设 $x_{1}$ ， $x_{2}$ 是 $h (x) = f (x) - (3 a - 2) l n x - 3 x$ 的两个不同零点，证明： $a (x_{1} + x_{2}) > 4$ .

查看试题解析
22. 数学上有很多美丽的曲线令人赏心悦目，例如，极坐标方程 $ρ = a (1 + c o s θ)$ （ $a > 0$ ）表示的曲线为心形线，它对称优美，形状接近心目中的爱心图形.以极点 $O$ 为原点，极轴为 $x$ 轴的正半轴建立直角坐标系，直线 $l$ 的参数方程为 ${\begin{array}{l} x = \frac{1}{2} t ， \\ y = \frac{\sqrt{3}}{2} t \end{array}$ （ $t$ 为参数）.

(1)、求直线 $l$ 的极坐标方程和心形线的直角坐标方程；

(2)、已知点 $P$ 的极坐标为 $(2 ， 0)$ ，若 $P$ 为心形线上的点，直线 $l$ 与心形线交于 $A$ ， $B$ 两点（异于 $O$ 点），求 $△ A B P$ 的面积.

查看试题解析
23. 已知 $a$ ， $b$ 均为正数，且 $a^{2} + 2 b^{2} = 6$ ，证明：

(1)、 $a + 2 b \leq 3 \sqrt{2}$ ；

(2)、 $\frac{1}{a} + \frac{2}{b} \geq \frac{3}{2} \sqrt{2}$ ．

查看试题解析

年龄/岁	$[20 ， 30)$	$[30 ， 40)$	$[40 ， 50)$	$[50 ， 60)$	$[60 ， 70]$
频数	15	25	30	20	10
满意	13	20	27	16	4

	年龄低于50岁的人数	年龄不低于50岁的人数	合计
满意
不满意
合计

$P (K^{2} \geq k_{0})$	0.10	0.05	0.01	0.001
$k_{0}$	2.706	3.841	6.635	10.828