湖北省十堰市2022-2023学年高一上学期数学期末试卷

试卷更新日期：2023-03-15 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x ∣ x \geq - 1} ， B = {x ∣ - 1 \leq 10 - x \leq 12}$ ，则 $A \cup B =$ （）

A、 $[- 2 ， 11]$ B、 $[- 2 ， + \infty)$ C、 $[- 1 ， + \infty)$ D、 $[- 1 ， 11]$

查看试题解析
2. 关于命题 $p ：$ “ $\exists x \in N ， 6 x^{2} - 7 x + 2 \leq 0$ ”，下列判断正确的是（）

A、该命题是全称量词命题，且为假命题 B、该命题是存在量词命题，且为真命题 C、 $\neg p ： \forall x \in N ， 6 x^{2} - 7 x + 2 > 0$ D、 $\neg p ： \forall x \notin N ， 6 x^{2} - 7 x + 2 > 0$

查看试题解析
3. 已知角 $α$ 的顶点与坐标原点 $O$ 重合，始边与 $x$ 轴的非负半轴重合．若角 $α$ 终边上一点 $P$ 的坐标为 $(- c o s \frac{π}{3} ， s i n \frac{π}{6})$ ，则 $t a n α =$ （）

A、 $- \frac{\sqrt{2}}{2}$ B、1 C、 $\frac{\sqrt{2}}{2}$ D、 $- 1$

查看试题解析
4. 已知幂函数的图象经过点 $P (2 ， \frac{1}{4})$ ，则该幂函数的大致图象是（）

A、 B、 C、 D、

查看试题解析
5. 若定义在 $R$ 上的函数 $f (x)$ 满足 $f (x) = {\begin{array}{l} 2023 ， x 为有理数， \\ 0 ， x 为无理数， \end{array}$ 则“ $x$ 为无理数”是“ $f (f (x)) =$ 2023”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
6. 已知第一象限内的点 $P (a ， b)$ 在一次函数 $y = - 8 x + 5$ 的图象上，则 $\frac{2}{a} + \frac{1}{b}$ 的最小值为（）

A、25 B、5 C、4 D、 $\frac{5}{2}$

查看试题解析
7. 黑洞原指非常奇怪的天体，它体积小､密度大､吸引力强，任何物体到了它那里都别想再出来，数字中也有类似的“黑洞”.任意取一个数字串，长度不限，依次写出该数字串中偶数的个数､奇数的个数以及总的数字个数，把这三个数从左到右写成一个新的数字串.重复以上工作，最后会得到一个反复出现的数字串，我们称它为“数字黑洞”，如果把这个数字串设为 $a$ ，则 $s i n (\frac{2 a}{3} π + \frac{π}{3}) =$ （）

A、 $\frac{\sqrt{3}}{2}$ B、 $- \frac{\sqrt{3}}{2}$ C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
8. 函数 $f (x) = \frac{1}{2^{x}} - l o g_{2} x + 1$ 的零点所在区间为（）

A、 $(0 ， 1)$ B、 $(1 ， 2)$ C、 $(2 ， 3)$ D、 $(3 ， 4)$

查看试题解析

二、多选题

9. 设 $a = 1 6^{0.3}$ ， $b = 9^{0.6}$ ， $c = l o g_{\sqrt{2}} \sqrt{3}$ ，则（）

A、 $a > c$ B、 $b > c$ C、 $a > b$ D、 $b > a$

查看试题解析
10. 已知定义在 $R$ 上的函数 $f (x)$ 在 $(- \infty ， 2]$ 上单调递增，且 $f (x + 2)$ 为偶函数，则（）

A、 $f (x)$ 的对称中心为 $(2 ， 0)$ B、 $f (x)$ 的对称轴为直线 $x = 2$ C、 $f (- 1) > f (4)$ D、不等式 $f (x + 3) > f (4 x)$ 的解集为 $(- \infty ， \frac{1}{5}) ∪ (1 ， + \infty)$

查看试题解析
11. 某城市有一个面积为1 $k m^{2}$ 的矩形广场，该广场为黄金矩形（它的宽与长的比为 $\frac{\sqrt{5} - 1}{2}$ ），在中央设计一个矩形草坪，四周是等宽的步行道，能否设计恰当的步行道宽度使矩形草坪为黄金矩形？下列选项不正确的是（）

A、步行道的宽度为 $\frac{\sqrt{5} - 1}{2}$ m B、步行道的宽度为 $\frac{\sqrt{5} + 1}{2}$ m C、步行道的宽度为5m D、草坪不可能为黄金矩形

查看试题解析
12. 高斯是德国的天才数学家，享有“数学王子”的美誉，以“高斯”命名的概念、定理、公式很多，如高斯函数 $y = [x]$ ，其中不超过实数x的最大整数称为x的整数部分，记作 $[x]$ ．如 $[2022] = 2022$ ， $[1.7] = 1$ ， $[- 1.5] = - 2$ ，记函数 $f (x) = x - [x]$ ，则（）

A、 $f (- 2.9) = 0.9$ B、 $f (x)$ 的值域为 $[0 ， 1)$ C、 $f (x)$ 在 $[0 ， 5]$ 上有5个零点 D、 $\forall a \in R$ ，方程 $f (x) + x = a$ 有两个实根

查看试题解析

三、填空题

13. 写出一个与 $130 °$ 终边相同的角：.

查看试题解析
14. 已知关于 $x$ 的一元二次不等式 $a x^{2} + b x + c < 0$ 的解集为 $(- \frac{1}{2} ， - \frac{1}{3})$ ，则关于 $x$ 的不等式 $b x^{2} - c x - a < 0$ 的解集为．

查看试题解析
15. 《乐府诗集》辑有晋诗一组，属清商曲辞吴声歌曲，标题为《子夜四时歌七十五首》.其中《夏歌二十首》的第五首曰：叠扇放床上，企想远风来.轻袖佛华妆，窈窕登高台.诗里的叠扇，就是折扇.一般情况下，折扇可看作是从一个圆面中剪下的扇形制作而成.如图，设扇形的面积为 $S_{1}$ ，其圆心角为 $θ$ ，圆面中剩余部分的面积为 $S_{2}$ ，当 $S_{1}$ 与 $S_{2}$ 的比值为 $\frac{\sqrt{5} - 1}{2}$ 时，扇面为“美观扇面”.若扇面为“美观扇面”，扇形的半径 $R =$ 10，则此时的扇形面积为.

查看试题解析
16. 若存在实数 $a ， b \in [1 ， 9]$ ，使得函数 $f (x) = | x + \frac{9}{x} - 10 | (x > 0)$ 在区间 $[a ， b]$ 上单调，且 $f (x)$ 在区间 $[a ， b]$ 上的取值范围为 $[m a ， m b]$ ，则 $m$ 的取值范围为.

查看试题解析

四、解答题

17. 计算：

(1)、 $5^{l o g_{5} 3} - l o g_{3} 11 \cdot l o g_{11} 27 + l o g_{8} 2 + l o g_{4} 8$ ；

(2)、若 $3^{m} - 3^{- m} = 2 \sqrt{3}$ ，求 $9^{m} + 9^{- m}$ 的值.

查看试题解析
18. 设全集为 $U = R$ ，集合 $A = {x ∣ x^{2} - 2 x - 15 \leq 0} ， B = {x ∣ x \leq - 5$ 或 $x \geq 3}$ .

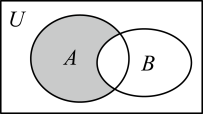(1)、求图中阴影部分表示的集合；

(2)、已知集合 $C = {x ∣ 10 - a < x < 2 a + 1}$ ，若 $(∁_{U} B) ∩ C = \emptyset$ ，求 $a$ 的取值范围.

查看试题解析
19. 已知角 $α$ 满足 $c o s α + 7 s i n α = 0$ .

(1)、若 $- \frac{π}{2} < α < 0$ ，求 $s i n α ， c o s α$ 的值；

(2)、若角 $β$ 的终边与角 $α$ 的终边关于 $x$ 轴对称，求 $\frac{s i n β - 3 c o s β}{2 s i n β + c o s β}$ 的值.

查看试题解析
20. 已知函数 $f (x) = l o g_{2} (\sqrt{x - 1} - a + 1)$ 的定义域为 $[1 ， + \infty)$ .

(1)、求 $y = 7 + a - \frac{4}{1 - a}$ 的最大值；

(2)、若 $a > 0$ ，求 $y = \frac{1}{2} a (3 - 2 a)$ 的最大值.

查看试题解析
21. 某地在曲线C的右上角区域规划一个科技新城，该地外围有两条相互垂直的直线形回道，为交通便利，计划修建一条连接两条国道和曲线C的直线形公路．记两条相互垂直的国道分别为 $l_{1}$ ， $l_{2}$ ，计划修建的公路为 $l$ ．如图所示， $A ， B$ 为C的两个端点，测得点A到 $l_{1}$ ， $l_{2}$ 的距离分别为5千米和20千米，点B到 $l_{1}$ ， $l_{2}$ 的距离分别为25千米和4千米．以 $l_{2}$ ， $l_{1}$ 所在的直线分别为x轴、y轴，建立平面直角坐标系 $x O y$ ．假设曲线C符合函数 $y = \frac{m}{x + n}$ （其中m，n为常数）模型．

(1)、求m，n的值．

(2)、设公路 $l$ 与曲线C只有一个公共点P，点P的横坐标为 $t$ ．
①请写出公路 $l$ 长度的函数解析式 $f (t)$ ，并写出其定义域．
②当 $t$ 为何值时，公路 $l$ 的长度最短？求出最短长度．

查看试题解析
22. 已知 $f (x) = \frac{4 x - a}{x^{2} + b}$ 是定义在 $R$ 上的奇函数，其中 $a ， b \in R$ ，且 $f (2) = 1$ .

(1)、求 $a ， b$ 的值；

(2)、判断 $f (x)$ 在 $[2 ， + \infty)$ 上的单调性，并用单调性的定义证明；

(3)、设 $g (x) = m x^{2} - 2 x + 2 - m$ ，若对任意的 $x_{1} \in [2 ， 4]$ ，总存在 $x_{2} \in [0 ， 1]$ ，使得 $f (x_{1}) = g (x_{2})$ 成立，求非负实数 $m$ 的取值范围.

查看试题解析