河南省信阳市2022-2023学年高二上学期数学期末教学质量检测试卷
试卷更新日期:2023-03-15 类型:期末考试
一、单选题
-
1. 直线的倾斜角为( )A、 B、 C、 D、2. 已知数列为等比数列,若 , , 则( )A、-4 B、2 C、4 D、3. 焦点坐标为的抛物线的标准方程为( )A、 B、 C、 D、4. 直线l的方向向量为 , 平面与的法向量分别为 , , 则下列选项正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则5. 蚊香具有悠久的历史,我国蚊香的发明与古人端午节的习俗有关.如图,为某校数学社团用数学软件制作的“蚊香”.画法如下:在水平直线上取长度为1的线段AB,作一个等边三角形ABC,然后以点B为圆心,AB为半径逆时针画圆弧交线段CB的延长线于点D(第一段圆弧),再以点C为圆心,CD为半径逆时针画圆弧交线段AC的延长线于点E,再以点A为圆心,AE为半径逆时针画圆弧…….以此类推,当得到的“蚊香”恰好有9段圆弧时,“蚊香”的长度为( )

 A、 B、 C、 D、6. 方程(m,n为常数)不能表示的曲线是( )A、直线 B、椭圆 C、双曲线 D、抛物线7. 直线与圆交于A,B两点,则( )A、2 B、 C、4 D、8. 已知正三棱柱的侧棱长为3,底面边长为2,则直线与侧面所成角的正弦值等于( )A、 B、 C、 D、9. 过点作直线l与双曲线交于点A,B,若P恰为AB的中点,则直线l的条数为( )A、0 B、1 C、2 D、不能确定10. 已知 , 是椭圆C的两个焦点,P为C上一点, , 若C的离心率为 , 则( )A、 B、 C、 D、11. 直线与曲线恰有2个公共点,则实数a的取值范围为( )A、 B、 C、 D、12. 如图,过抛物线的焦点为F的直线交抛物线于A,B两点,交其准线l于点C,若 , 且 , 则( )
A、 B、 C、 D、6. 方程(m,n为常数)不能表示的曲线是( )A、直线 B、椭圆 C、双曲线 D、抛物线7. 直线与圆交于A,B两点,则( )A、2 B、 C、4 D、8. 已知正三棱柱的侧棱长为3,底面边长为2,则直线与侧面所成角的正弦值等于( )A、 B、 C、 D、9. 过点作直线l与双曲线交于点A,B,若P恰为AB的中点,则直线l的条数为( )A、0 B、1 C、2 D、不能确定10. 已知 , 是椭圆C的两个焦点,P为C上一点, , 若C的离心率为 , 则( )A、 B、 C、 D、11. 直线与曲线恰有2个公共点,则实数a的取值范围为( )A、 B、 C、 D、12. 如图,过抛物线的焦点为F的直线交抛物线于A,B两点,交其准线l于点C,若 , 且 , 则( )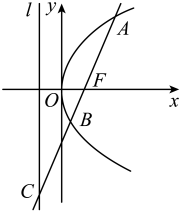 A、 B、 C、18 D、25
A、 B、 C、18 D、25二、填空题
-
13. 若向量与向量共线,则.14. 双曲线的渐近线方程是.15. 引江济淮是一项大型跨流域调水工程,2022年底试通航.如图是某段新开河渠的示意图.在二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB.已知 , , , , 则该二面角的大小为.
 16. “雪花曲线”是瑞典数学家科赫在1904年研究的一种分形曲线.如图是“雪花曲线”的一种形成过程:从一个正三角形开始,把每条边分成三等份,然后以各边的中间一段为底边分别向外作正三角形,再去掉底边,重复进行这一过程.
16. “雪花曲线”是瑞典数学家科赫在1904年研究的一种分形曲线.如图是“雪花曲线”的一种形成过程:从一个正三角形开始,把每条边分成三等份,然后以各边的中间一段为底边分别向外作正三角形,再去掉底边,重复进行这一过程.
如图,若第1个图中三角形的边长为1,则第3个图形的周长为;第n个图形的周长为.
三、解答题
-
17. 设等差数列的前n项和为 , 若 , .(1)、求的通项公式;(2)、求的最小值.18. 已知抛物线C:的焦点为F,点在C上, , 圆M:.(1)、求C与M的标准方程;(2)、过C上的点P作圆M的切线l,当l的倾斜角为时,求点P的坐标.19. 如图,四棱锥中,为等边三角形, , , , E为CD的中点,平面平面ABCD.
 (1)、求点E到平面PBC的距离;(2)、求平面PBC与平面PBE的夹角.
(1)、求点E到平面PBC的距离;(2)、求平面PBC与平面PBE的夹角.