河北省邯郸市魏县2022-2023学年高二上学期数学期末考试试卷
试卷更新日期:2023-03-15 类型:期末考试
一、单选题
-
1. 如图所示,在正方体中,点F是棱上的一个动点(不包括顶点),平面交棱于点E,则下列命题中正确的是( )
 A、存在点F,使得为直角 B、对于任意点F,都有直线∥平面 C、对于任意点F,都有平面平面 D、当点F由向A移动过程中,三棱锥的体积逐渐变大2. 已知与是直线为常数)上两个不同的点,则关于和的方程组的解的情况是( )A、无论如何,总是无解 B、无论如何,总有唯一解 C、存在 , 使之恰有两解 D、存在 , 使之有无穷多解3. 在平面直角坐标系中,已知点满足 , 记为点到直线的距离.当变化时,的最大值为( )A、1 B、2 C、3 D、44. 已知点在直线:上,过点的两条直线与圆:分别相切于两点,则圆心到直线的距离的最大值为( )A、 B、 C、 D、15. 已知为椭圆上不同的三点,直线 , 直线交于点 , 直线交于点 , 若 , 则( )A、0 B、 C、 D、6. 已知、为双曲线的左、右焦点,为双曲线的渐近线上一点,满足 , (为坐标原点),则该双曲线的离心率是( )A、 B、 C、 D、7. 点在直线上,若存在过的直线交抛物线于两点,且 , 则称点为“M点”,那么下列结论中正确的是( )A、直线上的所有点都是“点” B、直线上仅有有限个点是“M点” C、直线上的所有点都不是“M点” D、直线上有无穷多个点(但不是所有的点)是“点”8. 正整数数列中,由1开始依次按如下规则,将某些整数染成红色.先染1;再染3个偶数2,4,6;再染6后面最邻近的5个连续奇数7,9,11,13,15;再染15后面最邻近的7个连续偶数16,18,20,22,24,26,28;再染此后最邻近的9个连续奇数29,31,…,45;按此规则一直染下去,得到一红色子数列:1,2,4,6,7,9,11,13,15,16,……,则在这个红色子数列中,由1开始的第2021个数是( )A、3991 B、3993 C、3994 D、3997
A、存在点F,使得为直角 B、对于任意点F,都有直线∥平面 C、对于任意点F,都有平面平面 D、当点F由向A移动过程中,三棱锥的体积逐渐变大2. 已知与是直线为常数)上两个不同的点,则关于和的方程组的解的情况是( )A、无论如何,总是无解 B、无论如何,总有唯一解 C、存在 , 使之恰有两解 D、存在 , 使之有无穷多解3. 在平面直角坐标系中,已知点满足 , 记为点到直线的距离.当变化时,的最大值为( )A、1 B、2 C、3 D、44. 已知点在直线:上,过点的两条直线与圆:分别相切于两点,则圆心到直线的距离的最大值为( )A、 B、 C、 D、15. 已知为椭圆上不同的三点,直线 , 直线交于点 , 直线交于点 , 若 , 则( )A、0 B、 C、 D、6. 已知、为双曲线的左、右焦点,为双曲线的渐近线上一点,满足 , (为坐标原点),则该双曲线的离心率是( )A、 B、 C、 D、7. 点在直线上,若存在过的直线交抛物线于两点,且 , 则称点为“M点”,那么下列结论中正确的是( )A、直线上的所有点都是“点” B、直线上仅有有限个点是“M点” C、直线上的所有点都不是“M点” D、直线上有无穷多个点(但不是所有的点)是“点”8. 正整数数列中,由1开始依次按如下规则,将某些整数染成红色.先染1;再染3个偶数2,4,6;再染6后面最邻近的5个连续奇数7,9,11,13,15;再染15后面最邻近的7个连续偶数16,18,20,22,24,26,28;再染此后最邻近的9个连续奇数29,31,…,45;按此规则一直染下去,得到一红色子数列:1,2,4,6,7,9,11,13,15,16,……,则在这个红色子数列中,由1开始的第2021个数是( )A、3991 B、3993 C、3994 D、3997二、多选题
-
9. 下列结论正确的是( )A、 , B、若 ,则 C、若 ,则 D、若 , , ,则10. 圆和圆的交点为 , 则有( )A、公共弦所在直线方程为 B、公共弦的长为 C、线段中垂线方程为 D、为圆上一动点,则到直线距离的最大值为11. 已知双曲线右焦点为 , 过且垂直于x轴的直线与双曲线交于A,B两点,点 , 若为锐角三角形,则下列说法正确的是( )A、双曲线过点 B、直线与双曲线有两个公共点 C、双曲线的一条渐近线的斜率小于 D、双曲线的离心率取值范围为12. 若函数的图象上存在两个不同的点P,Q,使得在这两点处的切线重合,则称函数为“切线重合函数”,下列函数中是“切线重合函数”的是( )A、 B、 C、 D、
三、填空题
-
13. 阅读材料:空间直角坐标系中,过点且一个法向量为的平面的方程为 , 阅读上面材料,解决下面问题:已知平面的方程为 , 直线是两平面与的交线,则直线与平面所成角的正弦值为 .14. 已知为正方体表面上的一动点,且满足 , 则动点运动轨迹的周长为.15. 设是曲线上的点, , , 则的最大值等于 .16. 函数 , 定义数列如下: , 是过两点、的直线与x轴交点的横坐标,数列的通项公式为.
四、解答题
-
17. 如图,在多面体中,底面为正方形,平面 , 平面 , , .
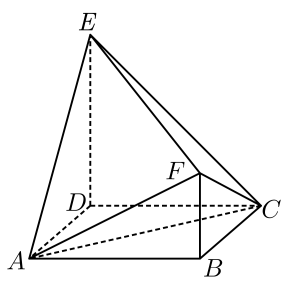 (1)、求证:平面;(2)、若 , 求与平面所成角的正弦值;(3)、若平面 , 求平面与平面夹角的余弦值.18. 已知在平面直角坐标系中,平面内动点P满足 .(1)、求点P的轨迹方程;(2)、点P轨迹记为曲线 , 若C,D是曲线与轴的交点,E为直线上的动点,直线CE,DE与曲线的另一个交点分别为M,N,直线MN与x轴交点为Q,求的最小值.19. 已知双曲线:的左、右焦点分别为、 , 直线过右焦点且与双曲线交于、两点.(1)、若双曲线的离心率为 , 虚轴长为 , 求双曲线的焦点坐标;(2)、设 , , 若的斜率存在,且 , 求的斜率;(3)、设的斜率为 , 且 , 求双曲线的离心率.20. 设为正实数,若各项均为正数的数列满足: , 都有 . 则称数列为数列.(1)、判断以下两个数列是否为数列:
(1)、求证:平面;(2)、若 , 求与平面所成角的正弦值;(3)、若平面 , 求平面与平面夹角的余弦值.18. 已知在平面直角坐标系中,平面内动点P满足 .(1)、求点P的轨迹方程;(2)、点P轨迹记为曲线 , 若C,D是曲线与轴的交点,E为直线上的动点,直线CE,DE与曲线的另一个交点分别为M,N,直线MN与x轴交点为Q,求的最小值.19. 已知双曲线:的左、右焦点分别为、 , 直线过右焦点且与双曲线交于、两点.(1)、若双曲线的离心率为 , 虚轴长为 , 求双曲线的焦点坐标;(2)、设 , , 若的斜率存在,且 , 求的斜率;(3)、设的斜率为 , 且 , 求双曲线的离心率.20. 设为正实数,若各项均为正数的数列满足: , 都有 . 则称数列为数列.(1)、判断以下两个数列是否为数列:数列:3,5,8,13,21;
数列: , , 5,10.
(2)、若数列满足且 , 是否存在正实数 , 使得数列是数列?若存在,求的取值范围;若不存在,说明理由.(3)、若各项均为整数的数列是数列,且的前项和为150,求的最小值及取得最小值时的所有可能取值.