河北省邯郸市2023届高三上学期数学期末试卷
试卷更新日期:2023-03-15 类型:期末考试
一、单选题
-
1. 已知集合 , , 若 , 则( )A、 B、 C、 D、2. 已知复数 , 则的虚部为( )A、 B、 C、 D、3. 已知向量的夹角为 , 且 , , 则( )A、 B、 C、 D、14. 已知幂函数满足 , 则的值为( )A、2 B、 C、 D、5. 已知圆柱的底面半径为2,母线长为8,过圆柱底面圆周上一点作与圆柱底面所成角为的平面,把这个圆柱分成两个几何体,则两几何体的体积之比为( )A、 B、 C、 D、6. 甲、乙两个家庭出去游玩,准备分别从北京、上海、重庆和天津4个地点中随机选择一个,记事件A:甲和乙选择的地点不同,事件B:甲和乙恰有一个选择北京,则( )A、 B、 C、 D、7. 三角形是生活中随处可见的简单图形,其中有非常有趣的特殊点及特殊线.大数学家欧拉在1765年发现,给定一个三角形,则其外心、重心、垂心落在同一条直线上,后人为了纪念欧拉,称这条直线为欧拉线.在平面直角坐标系xOy中,的顶点 , , 则“的欧拉线方程为”是“点C的坐标为”的( )A、必要不充分条件 B、充分不必要条件 C、充要条件 D、既不充分也不必要条件8. 已知 , , 且 , 则的最小值为( )A、10 B、9 C、 D、
二、多选题
-
9. 对两组数据进行统计后得到的散点图如图,关于其线性相关系数的结论正确的是( )
 A、 B、 C、 D、10. 在等差数列中, , 公差 , 则使其前n项和取得最小值的正整数n是( )A、4 B、5 C、6 D、711. 已知双曲线的上、下焦点分别为 , 点P在双曲线上且位于x轴上方,则下列结论正确的是( )A、线段的最小值为1 B、点P到两渐近线的距离的乘积为 C、若为直角三角形,则的面积为5 D、的内切圆圆心在直线上12. 如图,正方体的棱长为1,P是线段上的动点,则下列结论正确的是( )
A、 B、 C、 D、10. 在等差数列中, , 公差 , 则使其前n项和取得最小值的正整数n是( )A、4 B、5 C、6 D、711. 已知双曲线的上、下焦点分别为 , 点P在双曲线上且位于x轴上方,则下列结论正确的是( )A、线段的最小值为1 B、点P到两渐近线的距离的乘积为 C、若为直角三角形,则的面积为5 D、的内切圆圆心在直线上12. 如图,正方体的棱长为1,P是线段上的动点,则下列结论正确的是( )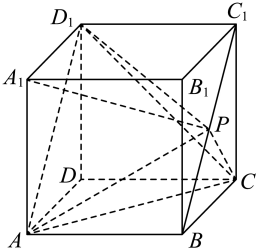 A、四面体的体积为定值 B、的最小值为 C、平面 D、当直线与AC所成的角最大时,四面体的外接球的体积为
A、四面体的体积为定值 B、的最小值为 C、平面 D、当直线与AC所成的角最大时,四面体的外接球的体积为三、填空题
-
13. 已知函数为奇函数,则实数.14. 已知 , 则.15. 近年来,加强青少年体育锻炼,重视体质健康已经在社会形成高度共识.2021年10月,《中华人民共和国体育法》在颁布20多年后迎来首次大修.教育部发布的2022年工作要点中提出,实施学校体育和体教融合改革发展行动计划.为了考察某校各班参加两项以上体育项目锻炼小组的人数,在全校随机抽取五个班级,把每个班级参加两项以上体育项目锻炼小组的人数作为样本数据.已知样本平均数为7,样本的标准差为2,若样本数据各不相同,则样本数据的第80百分位数是.16. 已知抛物线的焦点为F,若在抛物线C上,且满足 , 则的最小值为.
四、解答题
-
17. 在中,角A,B,C的对边分别是a,b,c,且满足.(1)、求A;(2)、若 , 求的取值范围.18. 设为数列的前n项和,已知 , .(1)、求数列的通项公式;(2)、若 , 记数列的前n项和为 , 证明:.19. 如图,在多面体中,为等边三角形,.
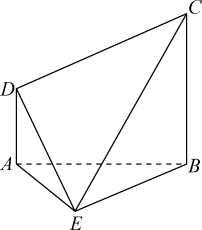 (1)、求证:平面平面;(2)、求直线与平面所成角的正弦值.20. 2022年卡塔尔世界杯是第二十二届世界杯足球赛,是历史上首次在卡塔尔和中东国家境内举行,也是第二次在亚洲举行的世界杯足球赛.11月22日,卡塔尔世界杯小组赛C组第1轮比赛中,梅西领衔的阿根廷队不敌沙特阿拉伯队.梅西在开场阶段打入一粒点球,但沙特在下半场开局后连入两球反超比分,这也是亚洲球队在本届世界杯上获得的首场胜利!为提升球队的射门技术,某足球队进行一次足球定点射门测试,规定每人最多踢3次,每次射门的结果相互独立.在A处射进一球得3分,在B处射进一球得2分,否则得0分.将队员得分逐次累加并用X表示,如果X的值不低于3分就判定为通过测试,立即停止射门,否则应继续射门,直到踢完三次为止.现有两种射门方案,方案1:先在A处踢一球,以后都在B处踢;方案2:都在B处踢球.已知甲队员在A处射门的命中率为 , 在B处射门的命中率为.(1)、若甲队员选择方案1,求他测试结束后所得总分X的分布列和数学期望;(2)、你认为甲队员选择哪种方案通过测试的可能性更大?说明理由.
(1)、求证:平面平面;(2)、求直线与平面所成角的正弦值.20. 2022年卡塔尔世界杯是第二十二届世界杯足球赛,是历史上首次在卡塔尔和中东国家境内举行,也是第二次在亚洲举行的世界杯足球赛.11月22日,卡塔尔世界杯小组赛C组第1轮比赛中,梅西领衔的阿根廷队不敌沙特阿拉伯队.梅西在开场阶段打入一粒点球,但沙特在下半场开局后连入两球反超比分,这也是亚洲球队在本届世界杯上获得的首场胜利!为提升球队的射门技术,某足球队进行一次足球定点射门测试,规定每人最多踢3次,每次射门的结果相互独立.在A处射进一球得3分,在B处射进一球得2分,否则得0分.将队员得分逐次累加并用X表示,如果X的值不低于3分就判定为通过测试,立即停止射门,否则应继续射门,直到踢完三次为止.现有两种射门方案,方案1:先在A处踢一球,以后都在B处踢;方案2:都在B处踢球.已知甲队员在A处射门的命中率为 , 在B处射门的命中率为.(1)、若甲队员选择方案1,求他测试结束后所得总分X的分布列和数学期望;(2)、你认为甲队员选择哪种方案通过测试的可能性更大?说明理由.