（人教版）2022-2023学年八年级数学下册18.1 平行四边形同步测试

试卷更新日期：2023-03-15 类型：同步测试

进入出卷网下载

一、单选题

1. 在平行四边形ABCD中，如果 $∠ A = 35 °$ ，那么 $∠ C$ 的度数是（）

A、 $145 °$ B、 $65 °$ C、 $55 °$ D、 $35 °$

查看试题解析
2. 如图，平行四边形ABCD的对角线AC与BD相交于点O，AB⊥AC．若AC＝6，BD＝10，则AB的长是（）

A、3 B、4 C、5 D、6

查看试题解析
3. 如图，四边形ABCD是平行四边形，点B在线段BC的延长的，若∠DCE=130°，则∠A=（）

A、40° B、50° C、130° D、都不对

查看试题解析
4. 如图，平行四边形ABCD的顶点A，B，C的坐标分别是（0， 2），（-1，-1）（2， -1），则顶点D的坐标是（）

A、（-3， 2） B、（3， -2） C、（3， 2） D、（2， 2）

查看试题解析
5. 如图，在▱ABCD中，AD＝5，AB＝3，AE平分∠BAD交BC边于点E，则线段BE，EC的长度分别为（）

A、2和3 B、3和2 C、4和1 D、1和4

查看试题解析
6. 如图，在△ABC中，D、E分别是AB、AC边上的中点，若DE＝4，则BC等于（）

A、2 B、4 C、8 D、12

查看试题解析
7. 如图四边形ABCD的对角线AC，BD交于点O，则不能判断四边形ABCD是平行四边形的是（）

A、AB∥CD，∠DAC=∠BCA B、AB=CD，∠ABO=∠CDO C、AC=2AO，BD=2BO D、AO=BO，CO=DO

查看试题解析
8. 如图，在Rt△ABC中，∠ACB＝90°，点D是斜边AB的中点，DE平分∠ADC，BC＝4，则DE的长是（）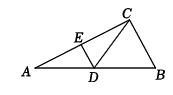

A、1 B、 $\sqrt{3}$ C、2 D、4

查看试题解析
9. 如图，在证明三角形的中位线定理时，小兰首先将原图形上面的三角形部分剪开，并旋转180°拼到下方．类似地，现有如图所示的四边形ABCD， $A D ∥ B C$ ，若 $A D = 3$ ， $B C = 7$ ， E、F分别是AB和DC的中点，则 $E F =$ （）

A、4 B、4.5 C、5 D、6

查看试题解析
10. 如图，已知△ABC是边长为3的等边三角形，点D是边BC上的一点，且BD＝1，以AD为边作等边△ADE，过点E作EF∥BC，交AC于点F，连接BF，则下列结论中①△ABD≌△BCF；②四边形BDEF是平行四边形；③S_四边形_BDEF $= \frac{\sqrt{3}}{2}$ ；④S_△_AEF $= \sqrt{3}$ ．其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 在平行四边形ABCD中，有两个内角的度数比为1：5，则平行四边形ABCD中较小内角的度数为．

查看试题解析
12. 如图，已知四边形 $A B C D$ 是平行四边形，对角线 $A C$ ， $B D$ 相交于点 $O$ ，添加一个条件，使平行四边形 $A B C D$ 是矩形（填一个即可）．

查看试题解析
13. 如图，在平行四边形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点O，在 $D C$ 的延长线上取点E，使 $C E = \frac{1}{2} C D$ ，连接 $O E$ 交 $B C$ 于点F，若 $B C = 12$ ，则 $C F =$ ．

查看试题解析
14. 如图， $△ A B C$ 是边长为1的等边三角形，取 $B C$ 边中点 $E$ ，作 $E D ∥ A B$ ， $E F ∥ A C$ ， $E D$ ， $E F$ 分别交 $A C$ ， $A B$ 于点 $D$ ， $F$ ，得到四边形 $E D A F$ ，它的面积记作 $S_{1}$ ；取 $B E$ 中点 $E_{1}$ ，作 $E_{1} D_{1} ∥ F B$ ， $E_{1} F_{1} ∥ E F$ ， $E_{1} D_{1}$ ， $E_{1} F_{1}$ 分别交 $E F$ ， $B F$ 于点 $D_{1}$ ， $F_{1}$ ，得到四边形 $E_{1} D_{1} F F_{1}$ ，它的面积记作 $S_{2}$ ……照此规律作下去，则 $S_{n} =$ ．

查看试题解析
15. 如图，平行四边形ABCD中，AC，BD相交于点O，E是AB的中点，若OE＝6，则AD＝．

查看试题解析

三、解答题

16. 如图，在 $▱ A B C D$ 中，点 $E$ 、 $F$ 在对角线 $A C$ 上，且 $A E = C F$ ，连接 $B F$ 、 $D E$ ．求证： $B F = D E$ ， $B F ∥ D E$ ．

查看试题解析
17. 如图，四边形ABCD是平行四边形，点E在BC上，点F在AD上，BE＝DF．求证：AE＝CF．

查看试题解析
18. 如图，在 $△ A B C$ 中，已知 $A B = 6$ ， $A C = 10$ ， $A D$ 平分 $∠ B A C$ ， $B D ⊥ A D$ 于点 $D$ ， $E$ 为 $B C$ 中点．求 $D E$ 的长．

查看试题解析

四、综合题

19. 如图，平行四边形ABCD中，AE平分 $∠ B A D$ 交BC于E，DF平分 $∠ A D C$ 交BC于F．

(1)、求证： $B F = E C$ ；

(2)、若E为BC的三等分点（靠近C点）， $A E = 2 \sqrt{3}$ ， $D F = 2$ ，求直线AB与CD之间的距离．

查看试题解析
20. 如图，在 $▱ A B C D$ 中， $A B = B D$ ，点 $E$ 在射线 $B D$ 上（不与 $B$ ， $D$ 重合）， $C F ∥ A E$ 交直线 $B D$ 于点 $F$ ．

(1)、如图1，当点 $E$ 在线段 $B D$ 上时，请直接写出 $B E$ ， $B F$ ， $C D$ 之间的数量关系；

(2)、如图2，当点 $E$ 在线段 $B D$ 的延长线上时，请写出 $B E$ ， $B F$ ， $C D$ 之间的数量关系，并加以证明．

查看试题解析
21. 如图，在 $△ A B C$ 中，D、E分别为AB、AC的中点，过点C作 $C F / / B D$ 交DE的延长线于点F．

(1)、求证：四边形BCFD为平行四边形；

(2)、若 $B C = 6$ ，求EF的长．

查看试题解析
22. 在四边形 $A B C D$ 中， $A C$ 、 $B D$ 交于点 $O$ ， $A D ∥ B C$ ， $B O = D O$ ．

(1)、证明：四边形 $A B C D$ 是平行四边形；

(2)、过点 $O$ 作 $O E ⊥ B D$ 交 $B C$ 于点 $E$ ，连接 $D E$ ．若 $∠ C D E = ∠ C B D = 15 °$ ，求 $∠ A B C$ 的度数．

查看试题解析
23. 已知：如图，在四边形ABCD中， $A B ∥ C D$ ，对角线AC、BD相交于点O，且O是AC的中点．

(1)、求证： $△ A O B$ ≌ $△ C O D$ ；

(2)、求证：四边形ABCD是平行四边形．

查看试题解析

（人教版）2022-2023学年八年级数学下册18.1 平行四边形 同步测试

一、单选题

二、填空题

三、解答题

四、综合题

（人教版）2022-2023学年八年级数学下册18.1 平行四边形同步测试