四川省达州市渠县2022-2023学年八年级下学期第一次月考数学测试题

试卷更新日期：2023-03-15 类型：月考试卷

进入出卷网下载

一、单选题（每小题3分，共30分）

1. 若a＜b，则下列结论不一定成立的是（）

A、 $a - 1 < b - 1$ B、 $2 a < 2 b$ C、 $- \frac{a}{3} > - \frac{b}{3}$ D、 $a^{2} < b^{2}$

查看试题解析
2. 到三角形三个顶点的距离相等的点是（）

A、三条中线的交点 B、三条高的交点 C、三条角平分线的交点 D、三条边的垂直平分线的交点

查看试题解析
3. 不等式 $3 (1 - x) > 2 - 4 x$ 的解在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
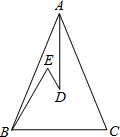
4. 如图，△ABC中，AC=BC，点D，E，F分别在边AC，AB，BC上，且满足AD=BE，AE=BF，∠DEF=40°，则∠C的度数是（）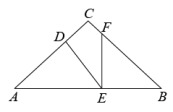

A、90° B、100° C、120° D、140°

查看试题解析
5. 关于x的方程5－a(1－x)＝8x－(3－a)x的解是负数，则a的取值范围是( )

A、a＜－4 B、a＞5 C、a＞－5 D、a＜－5

查看试题解析
6. 如图，AD是等边 $△ A B C$ 的中线， $A E = A D$ ，则 $∠ E D C$ 的度数为（）

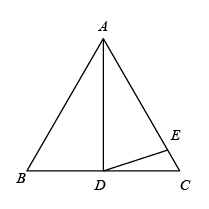A、30° B、20° C、25° D、15°

查看试题解析
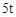7. 现用甲、乙两种运输车将搞旱物资运往灾区，甲种运输车载重，乙种运输车载重，安排车辆不超过10辆，则甲种运输车至少应安排（）

A、4辆 B、5辆 C、6辆 D、7辆

查看试题解析
8. 若不等式 $\frac{2 x + 5}{3} - 1 \leq 2 - x$ 的解集中x的每一个值，都能使关于x的不等式 $3 (x - 1) + 5 > 5 x + 2 (m + x)$ 成立，则m的取值范围是（）

A、 $m > - \frac{3}{5}$ B、 $m < - \frac{1}{5}$ C、 $m < - \frac{3}{5}$ D、 $m > - \frac{1}{5}$

查看试题解析
9.
如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为（　　）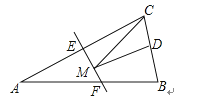

A、6 B、8 C、10 D、12

查看试题解析
10. 如图，过边长为1的等边三角形ABC的边AB上一点P，作 $P E ⊥ A C$ 于点E，Q为BC延长线上一点，当 $A P = C Q$ 时，PQ交AC于点D，则DE的长为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、不能确定

查看试题解析

二、填空题（每小题3分，共18分）

11. 用“>”或“<”填空：若，则a b.

查看试题解析
12. 已知等腰三角形一腰上的高与另一腰所在直线的夹角是 $40 °$ ，则底角的度数是.

查看试题解析
13. 如图，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ， AB=AC，分别过点B，C作经过点A的直线的垂线段BD，CE，若BD=5厘米，CE=8厘米，则DE的长为．

查看试题解析
14. 若关于x的不等式组 ${\begin{matrix} 2 x - 3 > 5 \\ x - m < 1 \end{matrix}$ 有3个整数解，则m的取值范围是 .

查看试题解析
15. 如图，直线 $y_{1} = a x + b$ 与直线 $y_{2} = m x + n$ 的交点是 $(- 1 ， 3)$ ，则不等式 $a x + b > m x + n$ 的解集是．

查看试题解析
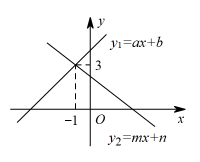16. 如图，在 $△ A B C$ 中，点D是BC边上一点，连接AD，把 $△ A B D$ 沿着AD翻折，得到 $△ A B^{'} D$ ， $B^{'} D$ 与AC交于点E，连接 $B B^{'}$ 交AD于点F，若 $D B^{'} = 3 D E$ ， $A B = 2 \sqrt{13}$ ， $A F = 6$ ， $△ A B^{'} E$ 的面积为12，则点B到 $D B^{'}$ 的距离为.

查看试题解析

三、解答题（共72分）

17. 解下列不等式，并把它的解集在数轴上表示出来．

(1)、 $\frac{5 x - 1}{3}$ ＜x+1，

(2)、3x-1≥2（x-1）

(3)、x-1≥ $\frac{x - 2}{2}$ +3．

查看试题解析
18. 解不等式组 ${\begin{array}{l} 1 - 2 (x - 1) ⩽ 5 \\ \frac{3 x - 2}{2} < x + \frac{1}{2} \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析
19. 如图，在△ABC中， $A B = A C$ ， D、E是△ABC内的两点，AD平分∠BAC， $∠ E B C = ∠ E = 60 °$ ．若 $B E = 6 c m$ ， $D E = 2 c m$ ，求BC的长．

查看试题解析
20. 已知关于x、y的方程组 ${\begin{array}{l} x - y = a + 3 \\ 2 x + y = 5 a \end{array}$ 的解满足x＞y＞0，化简|a|+|3-a|．

查看试题解析
21. 已知关于x的不等式 $\frac{2 m - m x}{2} > \frac{1}{2} x - 1$ ．

(1)、当m=1时，求该不等式的解集；

(2)、m取何值时，该不等式有解，并求出解集．

查看试题解析
22. 如图1， $△ A B C$ 中， $A B = A C$ ，点D在AB上，且.

(1)、求 $∠ A$ 的大小；

(2)、如图2， $D E ⊥ A C$ 于E， $D F ⊥ B C$ 于F，连接EF交CD于点H，求证：CD垂直平分线段EF.

查看试题解析
23. 小杰到学校食堂买饭，看到A、B两窗口前面排队的人一样多（设为a人，a > 8），就站到A窗口队伍的后面. 过了2分钟，他发现A窗口每分钟有4人买了饭离开队伍，B窗口每分钟有6人买了饭离开队伍，且B窗口队伍后面每分钟增加5人.

(1)、此时，若小杰继续在A窗口排队，则他到达窗口所花的时间是多少（用含a的代数式表示）？

(2)、此时，若小杰迅速从A窗口队伍转移到B窗口队伍后面重新排队，且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少，求a的取值范围（不考虑其他因素）.

查看试题解析
24. 如图，已知， AC平分 $∠ M A N$ ，点B、D分别在AN、AM上.

(1)、如图①，若，请你探索线段AD，AB，AC之间的数量关系，并给出证明；

(2)、如图②，若，则（1）中的结论是否仍然成立？若成立，给出证明；若不成立，请说明理由.

查看试题解析
25. 在△ABC中，AB≠AC，∠ABC与∠ACB的平分线交于O点，MN经过点O，与AB，AC相交于点M，N，且MN∥BC．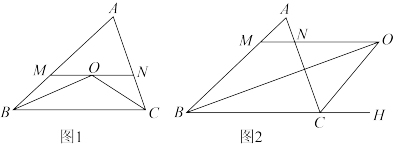

(1)、如图1，直接写出图中所有的等腰三角形；猜想：MN与BM，CN之间有怎样的数量关系，并说明理由．

(2)、如图2，△ABC中，∠ABC的平分线BO与三角形外角平分线CO交于点O，过O点作OM∥BC交AB于点M，交AC于点N．图中有等腰三角形吗？如果有，分别指出它们．写出MN与BM，CN之间的数量关系，并说明理由．

查看试题解析