四川省达州市大竹县2022-2023学年八年级下学期第一次月考数学测试题

试卷更新日期：2023-03-15 类型：月考试卷

进入出卷网下载

一、单选题（每小题3分，共30分）

1. 若a＞b，则下列不等式成立的是（）

A、a﹣3＜b﹣3 B、a＞b﹣1 C、 $\frac{a}{4} < \frac{b}{4}$ D、﹣2a＞﹣2b

查看试题解析
2. 等腰三角形周长为17cm，其中一边长为5cm，则该等腰三角形的腰长为（）

A、6cm B、7cm C、5cm或6cm D、5cm

查看试题解析
3. 在4，3，2，1，0，- $\frac{3}{2}$ ， $- \frac{10}{3}$ 中，能使不等式3x-2＞2x成立的数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 在下列解不等式 $\frac{2 + x}{3} > \frac{2 x - 1}{5}$ 的过程中，错误的一步是（）

A、去分母得 $5 (2 + x) > 3 (2 x - 1)$ B、去括号得 $10 + 5 x > 6 x - 3$ C、移项得 $5 x - 6 x > - 3 - 10$ D、系数化为 $1$ 得 $x > 13$

查看试题解析
5. 如图，DE、FG分别是△ABC的AB、AC边上的垂直平分线，且∠BAC＝100°，那么∠DAF的度数为（）

A、10° B、20° C、30° D、40°

查看试题解析
6. 不等式 $3 (x - 2) \leq x + 4$ 的非负整数解有个（）

A、4 B、5 C、6 D、无数个

查看试题解析
7. 如图，在△ABC中，边AB， AC的垂直平分线交于点P，连结BP，CP，若∠A= 50°，则∠BPC= ( ）.

A、50° B、100° C、130° D、150°

查看试题解析
8. 一次函数y＝kx+b（其中k＜0）的图象与x轴交于点A（-3，0），则关于x的不等式-kx+b＞0的解集为（）

A、x＞3 B、x＞-3 C、x＜3 D、x＜-3

查看试题解析
9. 如图，Rt△ABC中，∠ACB＝90°，∠BAC＝30°，∠ACB的平分线与∠ABC的外角平分线交于E点，连接AE，∠AEB的度数是（）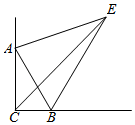

A、30° B、35° C、45° D、35°

查看试题解析
10. 若数m使关于x的不等式组 ${\begin{array}{l} \frac{3 + x}{2} - 1 \leq 3 \\ m - 2 x \leq - 2 \end{array}$ 有解且至多有3个整数解，且使关于y的分式方程 $\frac{3 y}{2 y - 4} = \frac{m - 2}{y - 2} + \frac{1}{2}$ 的解满足-3≤y≤4，则满足条件的所有整数m的个数是（　　）

A、6 B、5 C、4 D、3

查看试题解析

二、填空题（每小题3分，共18分）

11. 如图，在△ABC中，∠ACB＝90°，AD平分∠CAB，交边BC于点D，过点D作DE⊥AB，垂足为E．若∠CAD＝20°，则∠EDB的度数是．

查看试题解析
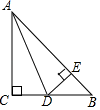12. 运行程序如图所示，规定：从“输入一个值x”到“结果是否＞94”为一次程序操作，如果程序操作进行了三次才停止，那么x的取值范围是．

查看试题解析
13. 在△ABC中，AB=5，BC=a，AC=b，如果a，b满足（a+5）(a-5)-b²=0，那么△ABC的形状是．

查看试题解析
14. 若不等式 $\frac{x + 5}{2} > - x - \frac{7}{2}$ 的解都能使不等式 $(m - 6) x < 2 m + 1$ 成立，则实数 $m$ 的取值范围是．

查看试题解析
15. 如图，已知：∠BAC的平分线与BC的垂直平分线相交于点D，DE⊥AB，DF⊥AC，垂足分别为E、F，AB＝6，AC＝3，则BE＝.

查看试题解析
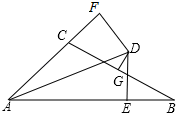16. 邮政部门规定：信函重100克以内（包括100克）每20克贴邮票0.8元，不足20克重以20克计算；超过100克，先贴邮票4元，超过100克部分每100克加贴邮票2元，不足100克重以100克计算．八（9）班有11位同学参加项目化学习知识竞赛，若每份答卷重12克，每个信封重4克，将这11份答卷分装在两个信封中寄出，所贴邮票的总金额最少是元．

查看试题解析

三、解答题．

17. 解不等式：

(1)、2x－7＞3（x－1）

(2)、 $\frac{x + 2}{4}$ - $\frac{2 x - 3}{6}$ ≥1

查看试题解析
18.
解不等式组 ${\begin{array}{l} 2 (x - 1) \geq x - 3 \\ \frac{3 x + 4}{5} > x \end{array}$ ，并在数轴上表示解集．

查看试题解析
19. 直角三角形的三边的长分别为a，b，c，其中c为斜边长，若 $\frac{a + b + c}{a + c} = \frac{4}{3}$ ，直角三角形的面积为 $\frac{3}{2}$ ，求它的各边长．

查看试题解析
20. 如图，已知线段a和∠EAF，点B在射线AE上．在∠EAF中画出△ABC，使点C在射线AF上，且BC＝a．

(1)、依题意将图补充完整；

(2)、如果∠A＝45°，AB＝4 $\sqrt{2}$ ， BC＝5，求△ABC的面积．

查看试题解析
21. 如图，在直角三角形ABC中，∠BCA＝90°，∠A＝60°，CD是角平分线，在CB上截取CE＝CA．

(1)、求证：DE＝BE；

(2)、若AC＝1，AD $= \sqrt{3} -$ 1，试求△ABC的面积．

查看试题解析
22. 某网店销售甲、乙两种防雾霾口罩，已知甲种口罩每袋的售价比乙种口罩多5元，小丽从该网店网购2袋甲种口罩和3袋乙种口罩共花费110元．

(1)、该网店甲、乙两种口罩每袋的售价各多少元？

(2)、根据消费者需求，网店决定用不超过10000元购进甲、乙两种口罩共500袋，且甲种口罩的数量大于乙种口罩的 $\frac{4}{5}$ ，已知甲种口罩每袋的进价为22.4元，乙种口罩每袋的进价为18元，请你帮助网店计算有几种进货方案？若使网店获利最大，应该购进甲、乙两种口罩各多少袋，最大获利多少元？

查看试题解析
23. 已知，如图，△ABC中，∠C＝90°，AB＝10，AC＝8，BD为∠ABC的角平分线交AC于D，过点D作DE垂直AB于点E，

(1)、求BC的长；

(2)、求AE的长；

(3)、求BD的长

查看试题解析
24. 如图，△ABC是以BC为斜边的等腰直角三角形，D为BC的中点，点E、F、G分别为线段AD、AB、BC上的一点．△EFG以E为直角顶点的等腰直角三角形，AB＝8．连结CE．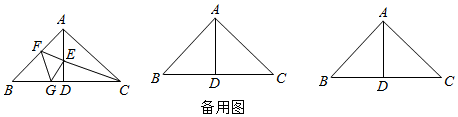

(1)、当G与点D重合时，求AE的长．

(2)、当DE＝2时，求△AEF的面积．

(3)、①比较△BGF与△CGE的面积大小关系，并说明理由．
②当△BGF的面积为6时，求BG的长．

查看试题解析
25. 数学兴趣小组根据学习函数的经验，对函数y＝ $\frac{x}{| x - 1 |}$ 的图象与性质进行了探究下面是他们的探究过程，请补充完整，并解决相关问题：

(1)、函数y＝ $\frac{x}{| x - 1 |}$ 的自变量x的取值范围是；

(2)、下表是y与x的几组对应值，则表中m的值为；

x

…

-3

-2

-1

0

$\frac{1}{2}$

$\frac{3}{4}$

$\frac{4}{5}$

$\frac{4}{3}$

$\frac{3}{2}$

2

4

5

…

y

…

- $\frac{3}{4}$

- $\frac{2}{3}$

m

0

1

3

4

4

3

2

$\frac{4}{3}$

$\frac{5}{4}$

…

(3)、根据上表数据，在如图所示的平面直角坐标系中描点画出函数y＝ $\frac{x}{| x - 1 |}$ 的图象，并写出这个函数的一条性质：；

(4)、画出函数y＝|x|的图象，结合函数图象，直接写出|x|≥ $\frac{x}{| x - 1 |}$ 时，x的取值范围．

查看试题解析

x	…	-3	-2	-1	0	$\frac{1}{2}$	$\frac{3}{4}$	$\frac{4}{5}$	$\frac{4}{3}$	$\frac{3}{2}$	2	4	5	…
y	…	- $\frac{3}{4}$	- $\frac{2}{3}$	m	0	1	3	4	4	3	2	$\frac{4}{3}$	$\frac{5}{4}$	…