(人教版)2022-2023学年七年级数学下册9.3 一元一次不等式组 同步测试
试卷更新日期:2023-03-15 类型:同步测试
一、单选题
-
1. 不等式组的解集在数轴上表示为( )A、
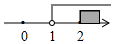 B、
B、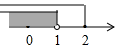 C、
C、 D、
D、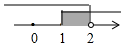 2. 不等式组的整数解有4个,则a的取值可能是( )A、1 B、2 C、-2 D、-33. 橘子是我们常见的一种水果,取5个大小均等的橘子放在同一简易天平秤,如图,则估计一个橘子的重量大约是( )
2. 不等式组的整数解有4个,则a的取值可能是( )A、1 B、2 C、-2 D、-33. 橘子是我们常见的一种水果,取5个大小均等的橘子放在同一简易天平秤,如图,则估计一个橘子的重量大约是( ) A、20 B、30 C、40 D、454. 运行程序如图所示,规定:从“输入一个值x”到“结果是否95”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是( )
A、20 B、30 C、40 D、454. 运行程序如图所示,规定:从“输入一个值x”到“结果是否95”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是( ) A、 B、 C、 D、5. 若关于的一元一次不等式组的解集是 , 且为非正整数,则满足条件的的取值有( )个.A、1 B、2 C、3 D、46. 把一些书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人就分不到3本,共有( )名同学.A、5 B、6 C、7 D、87. 若关于x的不等式组的解集为﹣3<x<2,则a+b的值为( )A、﹣5 B、5 C、6 D、﹣68. 把一些图书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人至少有一本,但不到3本.那么这些图书有( ).A、26本 B、25本 C、24本 D、23本9. 不等式组的解集在数轴上表示为( )A、
A、 B、 C、 D、5. 若关于的一元一次不等式组的解集是 , 且为非正整数,则满足条件的的取值有( )个.A、1 B、2 C、3 D、46. 把一些书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人就分不到3本,共有( )名同学.A、5 B、6 C、7 D、87. 若关于x的不等式组的解集为﹣3<x<2,则a+b的值为( )A、﹣5 B、5 C、6 D、﹣68. 把一些图书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人至少有一本,但不到3本.那么这些图书有( ).A、26本 B、25本 C、24本 D、23本9. 不等式组的解集在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 10. 若数a既使得关于x、y的二元一次方程组有正整数解,又使得关于x的不等式组的解集为x≥15,那么所有满足条件的a的值之和为( )A、﹣15 B、﹣30 C、﹣10 D、0
10. 若数a既使得关于x、y的二元一次方程组有正整数解,又使得关于x的不等式组的解集为x≥15,那么所有满足条件的a的值之和为( )A、﹣15 B、﹣30 C、﹣10 D、0二、填空题
-
11. 运行程序如图所示,规定:从“输入一个值x”到“结果是否>5”为一次程序操作,如果程序操作进行了两次才停止,那么x的取值范围是 .
 12. 已知不等式组的解集是 , 则关于的方程的解为.13. 已知关于x,y的方程组的解满足 , , 则m的取值范围为 .14. 已知关于 , 的方程组的解为整数,且关于的不等式组有且仅有3个整数解,则所有满足条件的整数a的和为.15. 已知不等式组的解集为 , 则m的取值范围是 .
12. 已知不等式组的解集是 , 则关于的方程的解为.13. 已知关于x,y的方程组的解满足 , , 则m的取值范围为 .14. 已知关于 , 的方程组的解为整数,且关于的不等式组有且仅有3个整数解,则所有满足条件的整数a的和为.15. 已知不等式组的解集为 , 则m的取值范围是 .三、解答题
-
16. 解不等式组: , 并将其解集在数轴上表示出来.
 17. 解不等式组 , 在数轴上表示出解集,并写出该不等式组的非负整数解.
17. 解不等式组 , 在数轴上表示出解集,并写出该不等式组的非负整数解. 18. 求不等式组
18. 求不等式组的整数解.
四、综合题
-
19. 某工厂有甲种原料66千克.乙种原料66.4千克,现计划用这两种原料生产A、B两种型号的产品共90件、已知每件A型号下需要甲种原料0.5千克,乙种原料0.8千克;每件B型号产品需要甲种原料1.2千克,乙种原料0.6千克.(1)、该工厂有哪几种生产方案?(2)、在这批产品全部售出的条件下,若1件A型号产品获利30元,1件B型号产品获利20元,(1)中哪种方案获利最大?最大利润是多少?(3)、在(2)的条件下,工厂决定将所获利润的25%全部用于再次购进甲、乙两种(两种原料都有)原料,且购进每种原料的数量均为正整数.若甲种原料每千克35元,乙种原料每千克55元.请直接写出购买甲、乙两种原料各多少千克20. 已知:关于、的方程组:(1)、求这个方程组的解:(用含有字母的代数式表示)(2)、若这个方程组的解满足为非负数,为负数,求字母的取值范围21. 南京火车货运站现有甲种货物1530吨,乙种货物1150吨,某公司将安排一列火车将这批货物运往上海,这列火车可挂、两种不同型号货厢50节(1)、已知甲种货物35吨和乙种货物15吨可装满一节型货厢,甲种货物25吨和乙种货物35吨可装满一节型货厢,运输这批货物有几种安排货厢方案?(2)、若一节型货厢的运费是0.5万元,一节型货厢的运费是0.8万元,如何安排运输方案,才能使得运费最少?并求出最少运费.22. 已知关于x,y的方程组(1)、当时,求m的值;(2)、若x为非负数,y为负数,求m的取值范围.23. 某景区的门票每张8元,一次性使用,考虑到人们的不同需求,也为了吸引更多的游客,该景区除保留原来的售票方法外,还推出了一种“购买个人年票”(个人年票从购买日起,可供持票者使用一年)的售票方法,年票分A,B,C三类:A类年票每张100元,持票者进入景区时,无需再购买门票;B类年票每张50元,持票者进入该景区时,需再购买门票,每次2元;C类年票每张20元,持票者进入该景区时,需再购买门票,每次3元.(1)、如果只能选择一种购买门票的方式,并且计划在一年中花费80元在该景区的门票上,通过计算,找出可进入该景区次数最多的方式.(2)、一年中进入该景区不少于多少次时,购买A类年票比较合算?