陕西省宝鸡市陈仓区2022-2023学年九年级上学期期末质量检测数学试题
试卷更新日期:2023-03-15 类型:期末考试
一、单选题
-
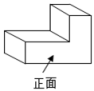
1. 方程的解是( )A、 , B、 , C、 , D、 ,2. 如图所示的几何体,其俯视图是( )
 A、
A、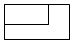 B、
B、 C、
C、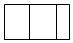 D、
D、 3. 矩形具有而菱形不一定具有的性质是( )A、对角线互相垂直 B、对角线相等 C、对角线互相平分 D、邻边相等4. 某养鸭场有若干只鸭,某天捉到30只全部做上标记,又过了一段时间,捉到50只,其中有2只有标记,那么估计该养鸭场有鸭子( )A、500只 B、650只 C、750只 D、900只5. 如图,AB∥CD∥EF,若= , BD=9,则DF的长为( )
3. 矩形具有而菱形不一定具有的性质是( )A、对角线互相垂直 B、对角线相等 C、对角线互相平分 D、邻边相等4. 某养鸭场有若干只鸭,某天捉到30只全部做上标记,又过了一段时间,捉到50只,其中有2只有标记,那么估计该养鸭场有鸭子( )A、500只 B、650只 C、750只 D、900只5. 如图,AB∥CD∥EF,若= , BD=9,则DF的长为( )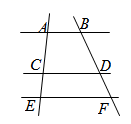 A、2 B、4 C、6 D、86. 一元二次方程的根的情况是( )A、只有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根7. 如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为( )
A、2 B、4 C、6 D、86. 一元二次方程的根的情况是( )A、只有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根7. 如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为( ) A、24 cm2 B、20 cm2 C、16 cm2 D、12 cm28. 我国快递业务逐年增加,2019年至2021年我国快递业务收入由7500亿元增加到9000亿元.设我国2019年至2021年快递业务收入的年平均增长率为x , 则可列方程为( )A、 B、 C、 D、9. 如图,以点O为位似中心,将△ABC缩小后得△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )
A、24 cm2 B、20 cm2 C、16 cm2 D、12 cm28. 我国快递业务逐年增加,2019年至2021年我国快递业务收入由7500亿元增加到9000亿元.设我国2019年至2021年快递业务收入的年平均增长率为x , 则可列方程为( )A、 B、 C、 D、9. 如图,以点O为位似中心,将△ABC缩小后得△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )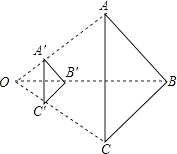 A、1:3 B、3:1 C、9:1 D、1:910.
A、1:3 B、3:1 C、9:1 D、1:910.如图,在Rt△ABC中∠C=90°,放置边长分别为4、6、x的三个正方形,则x的值为( )
 A、24 B、12 C、10 D、8
A、24 B、12 C、10 D、8二、填空题
-
11. 若 ,则 的值为.12. “双减”政策后,各校积极探索“课内提质增效,课后丰富多彩”的有效策略,某校的课后服务活动设置了四大板块课程: . 体育活动;劳动技能;经典阅读;科普活动.若小明和小亮两人随机选择一个板块课程,则两人所选的板块课程恰好相同的概率是 .13. 如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为°.
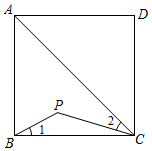 14. 反比例函数的图象经过点 , 图象上有两个点的坐标为 , 则与的大小关系为.15. 如图,在矩形中, , , , 将沿翻折,使点A落在点处,作射线 , 交的延长线于点F,则的长为.
14. 反比例函数的图象经过点 , 图象上有两个点的坐标为 , 则与的大小关系为.15. 如图,在矩形中, , , , 将沿翻折,使点A落在点处,作射线 , 交的延长线于点F,则的长为.
三、解答题
-
16. 解方程:17. 已知关于x的一元二次方程的两个实数根分别为 , , 求的值.18. 如图,已知矩形ABCD , 请用尺规作图法,在对角线AC上求作一点P , 使.(保留作图痕迹,不写做法).
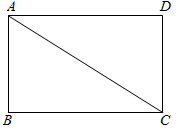 19. 如图,在菱形中,分别延长、到E、F,使得 , 连接、.求证:.
19. 如图,在菱形中,分别延长、到E、F,使得 , 连接、.求证:.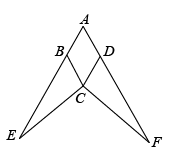 20. 已知关于x的一元二次方程:x2-(m-3)x-m=0.(1)、证明:无论m为何值,原方程有两个不相等的实数根;(2)、当方程有一根为1时,求m的值及方程的另一根.21. 甲乙两人报名参加疫情防控志愿者活动,他们将被随机分配到A、B、C、D四个小区协助医务人员做核酸检测工作.(1)、甲被派到C小区的概率是;(2)、请用画树状图或列表的方法求甲被派到B小区,同时乙被派到D小区的概率.22. 如图,郑明同学站在A处,测得他在路灯OC下影子AP的长与他的身高相等,都为1.5m,他向路灯方向走1m到B处时发现影子刚好落在A点.
20. 已知关于x的一元二次方程:x2-(m-3)x-m=0.(1)、证明:无论m为何值,原方程有两个不相等的实数根;(2)、当方程有一根为1时,求m的值及方程的另一根.21. 甲乙两人报名参加疫情防控志愿者活动,他们将被随机分配到A、B、C、D四个小区协助医务人员做核酸检测工作.(1)、甲被派到C小区的概率是;(2)、请用画树状图或列表的方法求甲被派到B小区,同时乙被派到D小区的概率.22. 如图,郑明同学站在A处,测得他在路灯OC下影子AP的长与他的身高相等,都为1.5m,他向路灯方向走1m到B处时发现影子刚好落在A点. (1)、请在图中画出形成影子的光线,并确定光源O的位置;(2)、求路灯OC的高.23. 如图,一次函数与反比例函数的图象相交于 , B两点,分别连接 , .
(1)、请在图中画出形成影子的光线,并确定光源O的位置;(2)、求路灯OC的高.23. 如图,一次函数与反比例函数的图象相交于 , B两点,分别连接 , .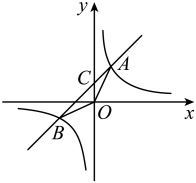 (1)、求这个反比例函数的表达式(2)、求的面积.24. 如图,点O是菱形ABCD对角线的交点,过点C作CE∥OD , 过点D作DE∥AC , CE与DE相交于点E.
(1)、求这个反比例函数的表达式(2)、求的面积.24. 如图,点O是菱形ABCD对角线的交点,过点C作CE∥OD , 过点D作DE∥AC , CE与DE相交于点E.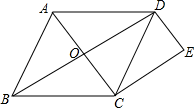 (1)、求证:四边形OCED是矩形.(2)、若AB=4,∠ABC=60°,求矩形OCED的面积.25. 某商场将原来每件进价80元的某种商品按每件100元出售,一天可出售100件,后来经过市场调查,发现这种商品单价每降低2元,其销量可增加20件.(1)、求商场经营该商品原来一天可获利多少元?
(1)、求证:四边形OCED是矩形.(2)、若AB=4,∠ABC=60°,求矩形OCED的面积.25. 某商场将原来每件进价80元的某种商品按每件100元出售,一天可出售100件,后来经过市场调查,发现这种商品单价每降低2元,其销量可增加20件.(1)、求商场经营该商品原来一天可获利多少元?
(2)、若商场经营该商品一天要获得利润2160元,则每件商品应降价多少元?
26. (1)、如图1,在四边形ABCD中,点P为AB上一点, , 若 , , 则;(2)、如图2,四边形ABCD中, , , , 点E在线段BC上且 , 连接DE,作 , 交AB于点F,则四边形ADEF的面积是多少?(3)、如图3,四边形ABCD中, , 点C到AB的距离为10, , 且 . 当四边形ABCD的面积是61时,求CD的长度是多少?
(1)、如图1,在四边形ABCD中,点P为AB上一点, , 若 , , 则;(2)、如图2,四边形ABCD中, , , , 点E在线段BC上且 , 连接DE,作 , 交AB于点F,则四边形ADEF的面积是多少?(3)、如图3,四边形ABCD中, , 点C到AB的距离为10, , 且 . 当四边形ABCD的面积是61时,求CD的长度是多少?