浙江省宁波市慈溪市2022-2023学年九年级上学期期末数学试卷
试卷更新日期:2023-03-15 类型:期末考试
一、单选题
-
1. 美丽的冬奥雪花呈现出浪漫空灵的气质.如图,雪花图案是一个中心对称图形,也可以看成自身的一部分围绕它的中心依次旋转一定角度得到的,这个角的度数可以是( )
 A、 B、 C、 D、2. 抛物线的对称轴是( )A、直线 B、直线 C、直线 D、直线3. 下列诗句所描述的事件属于不可能事件的是( )A、黄河入海流 B、大漠孤烟直 C、汗滴禾下土 D、手可摘星辰4. 已知的半径为3,点P到圆心O的距离为d,若点P在圆外,则d的取值范围为( )A、 B、 C、 D、5. 如图,正六边形内接于 , 正六边形的周长是12,则的半径是( )
A、 B、 C、 D、2. 抛物线的对称轴是( )A、直线 B、直线 C、直线 D、直线3. 下列诗句所描述的事件属于不可能事件的是( )A、黄河入海流 B、大漠孤烟直 C、汗滴禾下土 D、手可摘星辰4. 已知的半径为3,点P到圆心O的距离为d,若点P在圆外,则d的取值范围为( )A、 B、 C、 D、5. 如图,正六边形内接于 , 正六边形的周长是12,则的半径是( ) A、1 B、 C、2 D、6. 如图,已知直线 , 直线 , 分别交直线a,b,c于A,B,C和D,E,F, , , , 则的长为( )
A、1 B、 C、2 D、6. 如图,已知直线 , 直线 , 分别交直线a,b,c于A,B,C和D,E,F, , , , 则的长为( ) A、15 B、12 C、10 D、87. 如图,由边长为1的小正方形组成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C和点D,则tan∠ADC=( )
A、15 B、12 C、10 D、87. 如图,由边长为1的小正方形组成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C和点D,则tan∠ADC=( )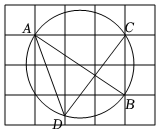 A、 B、 C、1 D、8. “圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长六寸,问径几何?”用现代的数学语言表述是:“为的直径,弦 , 垂足为E,寸,寸,求直径的长?”依题意得的长为( )
A、 B、 C、1 D、8. “圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长六寸,问径几何?”用现代的数学语言表述是:“为的直径,弦 , 垂足为E,寸,寸,求直径的长?”依题意得的长为( ) A、4寸 B、5寸 C、8寸 D、10寸9. 二次函数图象经过点 , , 且 , 则m的取值范围是( )A、 B、或 C、 D、或10. 一个大矩形按如图方式分割成五个小矩形后仍是中心对称图形,且矩形矩形.设矩形与矩形的面积分别为m和n,则这个大矩形的面积一定可以表示为( )
A、4寸 B、5寸 C、8寸 D、10寸9. 二次函数图象经过点 , , 且 , 则m的取值范围是( )A、 B、或 C、 D、或10. 一个大矩形按如图方式分割成五个小矩形后仍是中心对称图形,且矩形矩形.设矩形与矩形的面积分别为m和n,则这个大矩形的面积一定可以表示为( )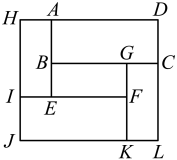 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若 , 则.12. 写出一个二次函数,满足图象开口向下,顶点在y轴上,且与x轴有两个交点:.13. 已知四边形内接于 , 若 , 则的度数为.14. 某批青稞种子在相同条件下发芽试验结果如下表:
每次试验粒数
50
100
300
400
600
1000
发芽频数
47
96
284
380
571
948
估计这批青稞发芽的概率是.(结果保留到0.01)
15. 如图,正方形的边长为6,点F为的中点,点E在上,且 , 在边上找一点P,使以E,D,P为顶点的三角形与相似,则的长为. 16. 如图,内接于 , , , 连接并延长至点E,使.
16. 如图,内接于 , , , 连接并延长至点E,使. (1)、 的半径为.(2)、若 , 则的长为.
(1)、 的半径为.(2)、若 , 则的长为.三、解答题
-
17.(1)、计算:;(2)、已知二次函数的图像过点和 , 求 , 的值.18. 宁波方特东方欲晓是一座以红色文化为主题的大型主题公园,公园精心策划了多个历史主题区域,其中最有特色的三个游玩项目如下表所示.
《圆明园》
《致远 致远》
《䳸击长空》
小慈和小溪两名同学去景区游玩,他们各自在这3个项目中任选一个进行游玩,每个项目被选择的可能性相同.
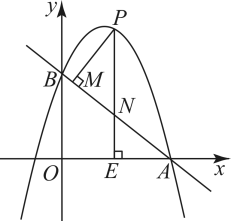
(1)、求小慈选择《致远 致远》的概率是多少?(2)、用画树状图或列表的方法,求小慈和小溪选择不同项目的概率.19. 如图是由边长为1的小正方形构成的的网格,△ABC的顶点A,B,C均在格点上. (1)、将绕C点按顺时针方向旋转 , 得到 , 请在图1中作出.(2)、在图2中,仅用无刻度直尺(不使用直角)在线段上找一点M,使得.(3)、在图3中,在三角形内寻找一格点N,使得.(请涂上黑点,注上字母)20. 如图,是的中线, , 过点作 , 垂足为点.
(1)、将绕C点按顺时针方向旋转 , 得到 , 请在图1中作出.(2)、在图2中,仅用无刻度直尺(不使用直角)在线段上找一点M,使得.(3)、在图3中,在三角形内寻找一格点N,使得.(请涂上黑点,注上字母)20. 如图,是的中线, , 过点作 , 垂足为点. (1)、求证:.(2)、若 , , 求的长.21. 如图,在中, , 以为直径的交于点 , 交的延长线于点.
(1)、求证:.(2)、若 , , 求的长.21. 如图,在中, , 以为直径的交于点 , 交的延长线于点.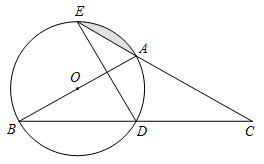 (1)、求证:点为线段的中点.(2)、若 , , 求的半径及阴影部分的面积.22. 如图1,一种手机支架可抽象成如图2的几何图形,水平底座长 , 伸缩臂长度可调节 , 并且可绕点A上下转动,转动角变动范围是 , 手机支撑片可绕点B上下转动, , 转动角变动范围是.小明使用该支架进行线上学习,当 , 且点C离底座的高度不小于7cm时,他才感觉舒适.
(1)、求证:点为线段的中点.(2)、若 , , 求的半径及阴影部分的面积.22. 如图1,一种手机支架可抽象成如图2的几何图形,水平底座长 , 伸缩臂长度可调节 , 并且可绕点A上下转动,转动角变动范围是 , 手机支撑片可绕点B上下转动, , 转动角变动范围是.小明使用该支架进行线上学习,当 , 且点C离底座的高度不小于7cm时,他才感觉舒适. (1)、如图3,当 , , 时,求托片底部点C离底座的高度,并判断是否符合小明使用的舒适要求.(参考数据 , , )(2)、如图2,当 , 的情况下,至少要伸缩到多少cm时才能恰好满足小明使用的舒适要求?(精确到1cm.参考数据)
(1)、如图3,当 , , 时,求托片底部点C离底座的高度,并判断是否符合小明使用的舒适要求.(参考数据 , , )(2)、如图2,当 , 的情况下,至少要伸缩到多少cm时才能恰好满足小明使用的舒适要求?(精确到1cm.参考数据)