备战2023年中考数学细点逐一突破真题训练第12章全等三角形
试卷更新日期:2023-03-15 类型:二轮复习
一、平移型
-
1. 如图,点B,F,C,E在一条直线上,BF=CE, , ∠A=∠D.求证:AC=DF.
 2. 如图,点E、C在线段BF上,AC∥DF,∠A=∠D,AB=DE,证明:BE=CF.
2. 如图,点E、C在线段BF上,AC∥DF,∠A=∠D,AB=DE,证明:BE=CF. 3. 已知:如图,点E、F在CD上,且 , , .
3. 已知:如图,点E、F在CD上,且 , , .求证:≌ .
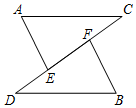 4. 如图, , 相交于点O,且 , .
4. 如图, , 相交于点O,且 , . (1)、求证:;(2)、若在直线上截取 , 求证: .
(1)、求证:;(2)、若在直线上截取 , 求证: .二、轴对称型
-
5. 如图,在△ABC中, , 点D、E在BC上,.求证:.
 6. 如图, , 则、两点间的距离为 m.
6. 如图, , 则、两点间的距离为 m.
三、旋转型
-
7. 如图,将△ABC绕点A逆时针旋转得到 ,点C的对应点为点 , 的延长线交BC于点D , 连接AD . 则下列说法错误的是( )
 A、 B、 C、 D、AD平分8. 已知:如图, , , 三点在同一直线上,和为等腰直角三角形, .
A、 B、 C、 D、AD平分8. 已知:如图, , , 三点在同一直线上,和为等腰直角三角形, . (1)、求证: , ;(2)、已知 , , 求的长.9. 如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接MC.
(1)、求证: , ;(2)、已知 , , 求的长.9. 如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接MC.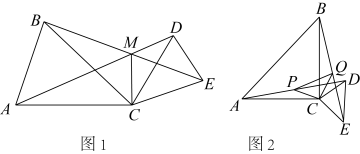 (1)、求证:BE=AD;(2)、用含α的式子表示∠AMB的度数(直接写出结果);(3)、当时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.10.
(1)、求证:BE=AD;(2)、用含α的式子表示∠AMB的度数(直接写出结果);(3)、当时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.10. (1)、如图1,与均是顶角为的等腰三角形,、分别是底边,求证:;(2)、如图2,和均为等边三角形,点A、D、E在同一直线上,连接 .
(1)、如图1,与均是顶角为的等腰三角形,、分别是底边,求证:;(2)、如图2,和均为等边三角形,点A、D、E在同一直线上,连接 .填空:的度数为;线段与之间的数量关系是 .
(3)、拓展探究如图3,和均为等腰直角三角形, , 点A、D、E在同一直线上,为中边上的高,连接 . 请判断的度数及线段、、之间的数量关系,并说明理由.
11. 如图,在边长为4的正方形内作 , 交于点 , 交于点 , 连接 , 将绕点顺时针旋转得到 .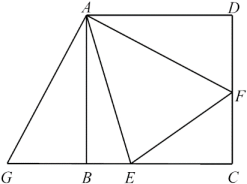 (1)、求证:;(2)、若 , 求的长.12. 在等腰中, , 点D在上,延长至点E,使 , 连接 .
(1)、求证:;(2)、若 , 求的长.12. 在等腰中, , 点D在上,延长至点E,使 , 连接 . (1)、若 ,
(1)、若 ,①如图1,求证:;
②如图2,将绕点C按顺时针方向旋转一定的角度,使点A,D,E三点在一条直线上,判定的形状,并说明理由.
(2)、若 , 如图3,(1)中①的结论是否成立?若不成立,请给出 , 之间的数量关系;若成立,请给出证明.四、一线三等角型
-
13. 如图,A、C、D三点共线,△ABC和△CDE落在AD的同侧,AC=CE,∠B=∠BCE=∠CDE.求证:AB=CD.
 14. 菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
14. 菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.(1)如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图2,若∠EAF=60°,求证:△AEF是等边三角形.
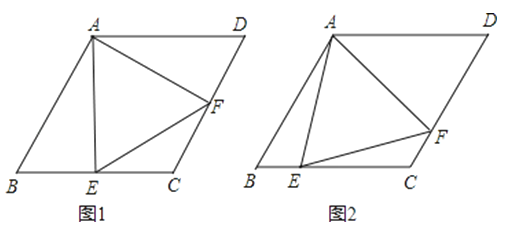 15. 如图,于点 , 点在直线上,.
15. 如图,于点 , 点在直线上,. (1)、如图1,若点在线段上,判断与的数量关系和位置关系,并说明理由;(2)、如图2,若点在线段的延长线上,其他条件不变,试判断(1)中结论是否成立,并说明理由.
(1)、如图1,若点在线段上,判断与的数量关系和位置关系,并说明理由;(2)、如图2,若点在线段的延长线上,其他条件不变,试判断(1)中结论是否成立,并说明理由.五、其他类型(半角模型,截长补短,倍长中线等)
-
16. 如图,在中,D为上一点,E为中点,连接DE并延长至点F,使得 , 连接 .
 (1)、求证:;(2)、若 , 连接平分平分 , 求的度数.17. 如图,是等边三角形,是等腰三角形,且 , , 以D为顶点作一个60°角,角的两边分别交 , 边于M,N两点,连接 , 延长至E,使 , 连接 .
(1)、求证:;(2)、若 , 连接平分平分 , 求的度数.17. 如图,是等边三角形,是等腰三角形,且 , , 以D为顶点作一个60°角,角的两边分别交 , 边于M,N两点,连接 , 延长至E,使 , 连接 . (1)、请在横线上写出角的度数,补充的证明过程.
(1)、请在横线上写出角的度数,补充的证明过程.证明:∵是等边三角形,∴ .
∵ , , ∴ .
∴ , .
∵ , ∴ .
即 ;
(2)、求证: .18. 如图,正方形ABCD中,点P,Q分别为CD,AD边上的点,且DQ=CP,连接BQ,AP.求证:BQ⊥AP. 19. 已知为等边三角形,是上的一点,是上的一点,且 , 直线相交于点 .
19. 已知为等边三角形,是上的一点,是上的一点,且 , 直线相交于点 . (1)、若是的中点,是的中点,如图①所示,求的度数(2)、若不是的中点,不是的中点,如图②所示,求的度数.
(1)、若是的中点,是的中点,如图①所示,求的度数(2)、若不是的中点,不是的中点,如图②所示,求的度数.六、全等三角形综合(拓展)
-
20. 是等边三角形,点D是上一点,点E在的延长线上,且 .
 (1)、如图1,当点D是的中点时,求证:;(2)、如图2,当点D是上任意一点时,取的中点F,连接 . 求的度数21. 如图,在中, , , 分别以 , 为边向外作正和正 , 连接 , , 当的边变化过程中,取最长时,则的长为.
(1)、如图1,当点D是的中点时,求证:;(2)、如图2,当点D是上任意一点时,取的中点F,连接 . 求的度数21. 如图,在中, , , 分别以 , 为边向外作正和正 , 连接 , , 当的边变化过程中,取最长时,则的长为. 22. 如图,△ABC中AC=BC,∠ACB=90° ,点D是BC上的动点(不与点B,C重合),过点C作CF⊥AD于E,交AB于点F,连接DF.
22. 如图,△ABC中AC=BC,∠ACB=90° ,点D是BC上的动点(不与点B,C重合),过点C作CF⊥AD于E,交AB于点F,连接DF. (1)、若∠CAD=30°,CD=8,求AE的长;(2)、求证:∠CAD=∠BCF;(3)、若点D是BC中点,求证:AD=CF+FD.23. 如图1,△ABC和△DCE都是等边三角形.
(1)、若∠CAD=30°,CD=8,求AE的长;(2)、求证:∠CAD=∠BCF;(3)、若点D是BC中点,求证:AD=CF+FD.23. 如图1,△ABC和△DCE都是等边三角形.探究发现
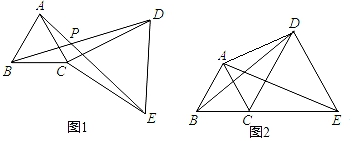 (1)、△BCD与△ACE是否全等?若全等,加以证明;若不全等,请说明理由.
(1)、△BCD与△ACE是否全等?若全等,加以证明;若不全等,请说明理由.拓展运用
(2)、若B、C、E三点不在一条直线上,∠ADC=30°,AD=3,CD=2,求BD的长.(3)、若B、C、E三点在一条直线上(如图2),且△ABC和△DCE的边长分别为1和2,求△ACD的面积及AD的长.24. 如图,中, , , 点为边上一点. (1)、如图1,若 , .
(1)、如图1,若 , .①求证:;
②若 , 求的值.
(2)、如图2,点为线段上一点,且 , , , 求的长.25. 在四边形中. (1)、如图1, , , , 分别是 , 上的点,且 , 探究图中 , , 之间的数量关系.
(1)、如图1, , , , 分别是 , 上的点,且 , 探究图中 , , 之间的数量关系.小林同学探究此问题的方法是:延长到点 , 使.连接 , 先对比与的关系,再对比与的关系,可得出、、之间的数量关系,他的结论是;
(2)、如图2,在四边形中, , , 、分别是 , 上的点,且 , 则上述结论是否仍然成立,请说明理由.(3)、如图3,在四边形中, , , 若点在的延长线上,点在的延长线上,若 , 请写出与的数量关系,并给出证明过程.