备战2023年中考数学细点逐一突破真题训练第11章三角形
试卷更新日期:2023-03-15 类型:二轮复习
一、三角形三边关系
-
1. 用一根小木棒与两根长分别为的小木棒组成三角形,则这根小木棒的长度可以为( )A、 B、 C、 D、2. 等腰三角形的两边长分别是 和 ,则它的周长是( )A、 B、 C、 或 D、以上都不对3. 若三角形两边长分别是3,6,则第三边 的取值范围是( )A、 B、 C、 D、无法确定4. 现有下列长度的五根木棒:3,5,8,10,13,从中任取三根,可以组成三角形的概率为 .5. 如图,是的中线,交的延长于点 , , , 则的取值可能是( )
 A、3 B、6 C、8 D、12
A、3 B、6 C、8 D、12二、三角形内角和及内外角关系
-
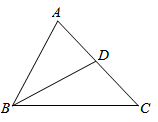
6. 如图,在中,平分 , , .求 , 的度数.
 7. 如图,在ABC中,AD是ABC的高,AE、BF是ABC角平分线,AE与BF相交于点O,∠BOA=125°,求∠DAC的度数.
7. 如图,在ABC中,AD是ABC的高,AE、BF是ABC角平分线,AE与BF相交于点O,∠BOA=125°,求∠DAC的度数. 8. 如图,在中,是的角平分线,是边上的高,相交于点O,如果 , 求的度数.
8. 如图,在中,是的角平分线,是边上的高,相交于点O,如果 , 求的度数.
三、三角形有关的重要线段
-
9. 下列四个图中,正确画出△ABC中BC边上的高是( )A、
 B、
B、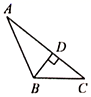 C、
C、 D、
D、 10. 如图,射线OC是∠AOB的平分线,P是射线OC上一点,PD⊥OA于点D,DP=6,若E是射线OB上一点,OE=4,则△OPE的面积是 .
10. 如图,射线OC是∠AOB的平分线,P是射线OC上一点,PD⊥OA于点D,DP=6,若E是射线OB上一点,OE=4,则△OPE的面积是 . 11. 利用直角三角板,作的高线,下列作法正确的是( )A、
11. 利用直角三角板,作的高线,下列作法正确的是( )A、 B、
B、 C、
C、 D、
D、 12. 如图,的面积为12,点D,E,F分别为的中点,则阴影部分的面积为( )
12. 如图,的面积为12,点D,E,F分别为的中点,则阴影部分的面积为( ) A、2 B、3 C、4 D、613. 如图,AD是△ABC的中线,E是AD上一点,BE交AC于F.若BE=AC,BF=9,CF=6,则AF的长度为 .
A、2 B、3 C、4 D、613. 如图,AD是△ABC的中线,E是AD上一点,BE交AC于F.若BE=AC,BF=9,CF=6,则AF的长度为 .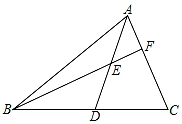 14. 如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,①△ABE的面积=△BCE的面积;②∠FAG=∠FCB;③AF=AG;④BH=CH.以上说法正确的是 .
14. 如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,①△ABE的面积=△BCE的面积;②∠FAG=∠FCB;③AF=AG;④BH=CH.以上说法正确的是 .
四、等腰三角形有关证明及计算
-
15. 等腰三角形一腰的中垂线与另一腰所在直线夹角为40°,该等腰三角形的底角的度数是.16. 下列说法不正确的是( )A、等腰三角形的对称轴是底边的垂直平分线 B、等腰直角三角形底边上的高线等于底边的一半 C、直角三角形中有一个角是30°,则这个角所对的直角边是斜边的一半 D、等边三角形有一条对称轴17. 如图,等边三角形ABC中,D、E分别为AB、BC边上的两个动点,且总使BD=CE,AE与CD交于点F,AG⊥CD于点G,则以下结论:(1)△ACE≌△CBD;(2)∠AFG=60°;(3)AF=2FG;(4)AC=2CE.其中正确的结论有( )个
 A、4 B、3 C、2 D、118. 如图,在△ABC中,AB=AC,AD⊥BC,∠BAD=28°,且AD=AE,求∠EDC的度数.
A、4 B、3 C、2 D、118. 如图,在△ABC中,AB=AC,AD⊥BC,∠BAD=28°,且AD=AE,求∠EDC的度数.
五、直角三角形有关证明及计算
-
19. 已知,如图,为等边三角形,相交于点.
 (1)、求证:;(2)、求的度数;(3)、若于 , 求的长.20. 如图,在△ABC中,AB=10,将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1 , 则阴影部分的面积为 .
(1)、求证:;(2)、求的度数;(3)、若于 , 求的长.20. 如图,在△ABC中,AB=10,将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1 , 则阴影部分的面积为 .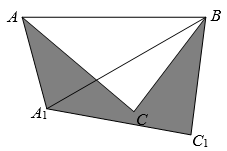 21. 如图,Rt△ACB中,∠ACB=90°,∠A=60°,CD、CE分别是△ABC的高和中线,下列说法错误的是( )
21. 如图,Rt△ACB中,∠ACB=90°,∠A=60°,CD、CE分别是△ABC的高和中线,下列说法错误的是( ) A、AD =AB B、S△CEB = S△ACE C、AC、BC的垂直平分线都经过E D、图中只有一个等腰三角形22. 如图,在△ABC中,∠CAB=30°,∠ACB=90°,AC=3,D为AB的中点,E为线段AC上任意一点(不与端点重合),当E点在线段AC上运动时,则DE+CE的最小值为.
A、AD =AB B、S△CEB = S△ACE C、AC、BC的垂直平分线都经过E D、图中只有一个等腰三角形22. 如图,在△ABC中,∠CAB=30°,∠ACB=90°,AC=3,D为AB的中点,E为线段AC上任意一点(不与端点重合),当E点在线段AC上运动时,则DE+CE的最小值为.
六、三角形的四心(内心、外心、重心、旁心)
-
23. 三角形的外心是三角形的( )A、三条中线的交点 B、三条角平分线的交点 C、三边垂直平分线的交点 D、三条高所在直线的交点24. 如图,△ABC的三边AB,BC,CA的长度分别为3,7,8,则△ABC的内切圆Ⅰ的半径为.
 25. 如图,在中, , 点是的内心,则度.
25. 如图,在中, , 点是的内心,则度.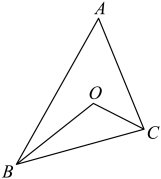 26. 如图,为的重心,过点作交于点 , 交于点 , 若 , 则四边形的面积为( )
26. 如图,为的重心,过点作交于点 , 交于点 , 若 , 则四边形的面积为( ) A、 B、1.5 C、2 D、327. 如图所示的网格由边长均为1的小正方形组成,点A、B、C、D、E、F在小正方形的顶点上,则外接圆的圆心是点 , 弧的长是.
A、 B、1.5 C、2 D、327. 如图所示的网格由边长均为1的小正方形组成,点A、B、C、D、E、F在小正方形的顶点上,则外接圆的圆心是点 , 弧的长是.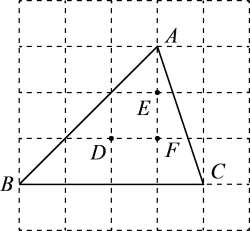 28. 在 中, , , ,点P是 所在平面内一点,则 取得最小值时,下列结论正确的是( )A、点P是 三边垂直平分线的交点 B、点P是 三条内角平分线的交点 C、点P是 三条高的交点 D、点P是 三条中线的交点29. 如图,在中,已知.
28. 在 中, , , ,点P是 所在平面内一点,则 取得最小值时,下列结论正确的是( )A、点P是 三边垂直平分线的交点 B、点P是 三条内角平分线的交点 C、点P是 三条高的交点 D、点P是 三条中线的交点29. 如图,在中,已知.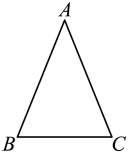 (1)、尺规作图;画的外接圆(保留作图痕迹,不写画法),(2)、连接若 , 求扇形的面积.
(1)、尺规作图;画的外接圆(保留作图痕迹,不写画法),(2)、连接若 , 求扇形的面积.七、三角形尺规作图题
-
30. 如图在的网格中,的顶点都在格点上.仅用无刻度的直尺在给定的网格中分别按下列要求画图.(请保留画图痕迹,画图过程用虚线表示,画图结果用实线表示)
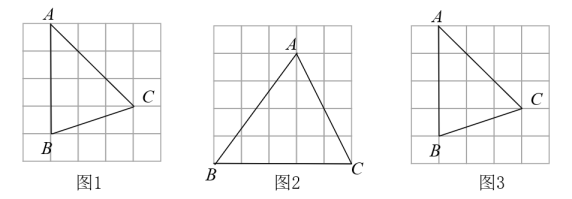 (1)、在图1中,画出的中线和重心G;(2)、在图2中,画线段 , 点E在上,使得;(3)、在图3中,画出的外心点O.
(1)、在图1中,画出的中线和重心G;(2)、在图2中,画线段 , 点E在上,使得;(3)、在图3中,画出的外心点O.