浙江省温州市瓯海区2023年中考第一次模拟考试数学试题
试卷更新日期:2023-03-15 类型:中考模拟
一、单选题
-
1. 计算的结果是( )A、-8 B、-4 C、-3 D、82. 某物体如图所示,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 不透明袋子中装有10个球,其中有6个红球和4个白球,它们除颜色外其余都相同.从袋子中随机摸出1个球,是红球的概率为( )A、 B、 C、 D、4. 某校参加课外兴趣小组的学生人数统计图如图所示.若信息技术小组有40人,则学科拓展小组有( )
3. 不透明袋子中装有10个球,其中有6个红球和4个白球,它们除颜色外其余都相同.从袋子中随机摸出1个球,是红球的概率为( )A、 B、 C、 D、4. 某校参加课外兴趣小组的学生人数统计图如图所示.若信息技术小组有40人,则学科拓展小组有( ) A、25人 B、40人 C、50人 D、60人5. 计算的结果是( )A、 B、 C、 D、6. 如图, , 分别切于B,C两点,若 , 则的度数为( )
A、25人 B、40人 C、50人 D、60人5. 计算的结果是( )A、 B、 C、 D、6. 如图, , 分别切于B,C两点,若 , 则的度数为( ) A、32° B、52° C、64° D、72°7. 甲、乙两位同学放学后走路回家,他们走过的路程(千米)与所用的时间(分)之间的函数关系如图所示.根据图中信息,下列说法正确的是( )
A、32° B、52° C、64° D、72°7. 甲、乙两位同学放学后走路回家,他们走过的路程(千米)与所用的时间(分)之间的函数关系如图所示.根据图中信息,下列说法正确的是( ) A、前10分钟,甲比乙的速度快 B、甲的平均速度为0.06千米/分钟 C、经过30分钟,甲比乙走过的路程少 D、经过20分钟,甲、乙都走了1.6千米8. 如图,一把梯子斜靠在墙上,端点A离地面的高度长为时,.当梯子底端点B沿水平方向向左移动到点 , 端点A沿墙竖直向上移动到点 , 设 , 则的长可以表示为( )
A、前10分钟,甲比乙的速度快 B、甲的平均速度为0.06千米/分钟 C、经过30分钟,甲比乙走过的路程少 D、经过20分钟,甲、乙都走了1.6千米8. 如图,一把梯子斜靠在墙上,端点A离地面的高度长为时,.当梯子底端点B沿水平方向向左移动到点 , 端点A沿墙竖直向上移动到点 , 设 , 则的长可以表示为( )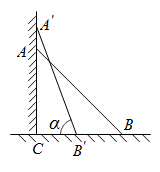 A、 B、 C、 D、9. 已知点 , 在反比例函数的图象上,其中 , 下列选项正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则10. 欧几里得《几何原本》中给出一种证明勾股定理的方法:“直角三角形斜边上正方形的面积等于两直角边上两个正方形的面积之和”.如图,中, , 四边形、四边形和四边形都是正方形,过点作的平行线交于点 , 连接 , , .若四边形的面积是四边形的面积的5倍,设与交于点 , 则的值是( )
A、 B、 C、 D、9. 已知点 , 在反比例函数的图象上,其中 , 下列选项正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则10. 欧几里得《几何原本》中给出一种证明勾股定理的方法:“直角三角形斜边上正方形的面积等于两直角边上两个正方形的面积之和”.如图,中, , 四边形、四边形和四边形都是正方形,过点作的平行线交于点 , 连接 , , .若四边形的面积是四边形的面积的5倍,设与交于点 , 则的值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式: .12. 关于的方程有两个相等的实数根,则的值是.13. 已知圆弧的度数为 , 弧长为 , 则圆的半径是.14. 一元一次不等式组的解是.15. 某超市销售一种饮料,每瓶进价为9元.经市场调查表明,当售价在10元到14元之间(含10元,14元)浮动时,日均销售量(瓶)与每瓶销售价(元)之间满足函数关系式.当销售价格定为每瓶元时,所得日均毛利润最大(每瓶毛利润=每瓶售价-每瓶进价).16. 甲、乙两幢完全一样的房子如图1,小聪与弟弟住在甲幢,为测量对面的乙幢屋顶斜坡M,N之间的距离,制定如下方案:两幢房子截面图如图2, , 小聪在离屋檐A处3m的点G处水平放置平面镜(平面镜的大小忽略不计),弟弟在离点G水平距离3m的点H处恰好在镜子中看到乙幢屋顶N,此时测得弟弟眼睛与镜面的竖直距离.下楼后,弟弟直立站在处,测得地面点F与E,M,N在一条直线上, , , , 则甲、乙两幢间距m,乙幢屋顶斜坡M,N之间的距离为m.

三、解答题
-
17.(1)、计算:;(2)、化简:.18. 如图,点A,D,B,E在同一条直线上, , , .
 (1)、求证:.(2)、设BC与DF交于点 , 若 , , 求的度数.19. 某商贸公司16名销售员上月完成的销售额情况如下:
(1)、求证:.(2)、设BC与DF交于点 , 若 , , 求的度数.19. 某商贸公司16名销售员上月完成的销售额情况如下:销售额(万元)
12
13
14
16
销售员人数
1
6
4
1
4
(1)、求这16名销售员上月销售额的平均数、中位数和众数.(2)、为使多数工人能顺利完成任务,现要从平均数、中位数和众数中选一个作为每月定额任务指标,你认为选哪一个统计量比较合适?请全面分析,并说明理由.20. 如图,在8×8的正方形网格中,已知的顶点都在格点上,请在所给网格中按要求画出图形. (1)、在图1中,将绕着点C顺时针方向旋转得到(点A,B的对应点分别为 , ),并画出.(2)、在图2中,以点C为位似中心,作的位似图形,并使边长放大到原来的2倍,请画出的位似图形.21. 已知二次函数的图象经过点 , .(1)、求该二次函数的表达式和图象顶点的坐标.(2)、若 , 是该二次函数图象上不同的两点.当时, , 求点Р到直线的距离.22. 在中,是钝角,交的延长线于点D,E,F分别为、的中点,.连接 , , 设与交于点O.
(1)、在图1中,将绕着点C顺时针方向旋转得到(点A,B的对应点分别为 , ),并画出.(2)、在图2中,以点C为位似中心,作的位似图形,并使边长放大到原来的2倍,请画出的位似图形.21. 已知二次函数的图象经过点 , .(1)、求该二次函数的表达式和图象顶点的坐标.(2)、若 , 是该二次函数图象上不同的两点.当时, , 求点Р到直线的距离.22. 在中,是钝角,交的延长线于点D,E,F分别为、的中点,.连接 , , 设与交于点O. (1)、求证:.(2)、若 , 时,求的长.23.
(1)、求证:.(2)、若 , 时,求的长.23.如何分配工作,使公司支付的总工资最少
素材1
某包装公司承接到21600个旅行包的订单,策划部准备将其任务分配给甲、乙两个车间去完成.由于他们的设备与人数不同,甲车间每天生产的总数是乙车间每天生产总数的2倍,甲车间单独完成这项工作所需的时间比乙车间单独完成少18天.

素材2
经调查,甲车间每人每天生产60个旅行包,乙车间每人每天生产40个旅行包.为提高工作效率,人事部到甲、乙两车间抽走相等数量的工人.策划部为了使抽走后甲、乙两车间每天生产的总数之和保持不变,余下的所有工人每天生产个数需要提高.因此,甲车间每天工资提高到3400元,乙车间每天工资提高到1560元.
问题解决
任务1
确定工作效率
求甲、乙车间原来每天分别生产多少个旅行包?
任务2
探究抽走人数
甲、乙每个车间被抽走了多少人?
任务3
拟定设计方案
甲、乙两车间抽走相等数量的工人后,按每人每天生产个数提高20%计算,如何安排甲、乙两车间工作的天数,使公司在完成该任务时支付的总工资最少?最少需要多少元?
24. 如图1,在正方形中,P是边上的动点,E在的外接圆上,且位于正方形的内部, , 连结. (1)、求证:是等腰直角三角形.(2)、如图2,连结 , 过点E作于点F,请探究线段与的数量关系,并说明理由.(3)、当Р是的中点时,.
(1)、求证:是等腰直角三角形.(2)、如图2,连结 , 过点E作于点F,请探究线段与的数量关系,并说明理由.(3)、当Р是的中点时,.①求的长.
②若点Q是外接圆的动点,且位于正方形的外部,连结.当与的一个内角相等时,求所有满足条件的的长.