四川省成都市锦江区2023年九年级一诊数学试题
试卷更新日期:2023-03-15 类型:中考模拟
一、单选题
-
1. 如图,是一个由长方体截去一部分后得到的几何体,其主视图是( )
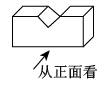 A、
A、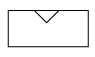 B、
B、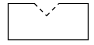 C、
C、 D、
D、 2. 下列函数中,y是x的反比例函数的是( )A、 B、 C、 D、3. 若关于x的一元二次方程x2﹣2x+m=0有一个解为x=﹣1,则另一个解为( )
2. 下列函数中,y是x的反比例函数的是( )A、 B、 C、 D、3. 若关于x的一元二次方程x2﹣2x+m=0有一个解为x=﹣1,则另一个解为( )
A、1 B、﹣3 C、3 D、44. 如图所示的两个四边形相似,则下列结论不正确的是( ) A、 B、 C、 D、5. 如图,已知在平面直角坐标系中,四边形是菱形,其中点B的坐标是 , 点D的坐标是 , 点A在x轴上,则点C的坐标是( )
A、 B、 C、 D、5. 如图,已知在平面直角坐标系中,四边形是菱形,其中点B的坐标是 , 点D的坐标是 , 点A在x轴上,则点C的坐标是( )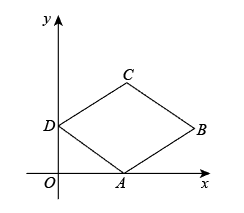 A、 B、 C、 D、6. 一个不透明的箱子里共装有m个球,其中红球5个,这些球除颜色不同外其余都相同.每次搅拌均匀后,任意摸出一个球记下颜色后再放回,大量重复试验发现,摸到红球的频率稳定在0.2附近,则可以估算出m的值为( )A、1 B、5 C、20 D、257. 如图,在方格纸上,以点O为位似中心,把线段缩小到原来的 , 则点A的对应点为( )
A、 B、 C、 D、6. 一个不透明的箱子里共装有m个球,其中红球5个,这些球除颜色不同外其余都相同.每次搅拌均匀后,任意摸出一个球记下颜色后再放回,大量重复试验发现,摸到红球的频率稳定在0.2附近,则可以估算出m的值为( )A、1 B、5 C、20 D、257. 如图,在方格纸上,以点O为位似中心,把线段缩小到原来的 , 则点A的对应点为( )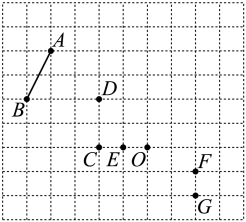 A、点D或点G B、点E或点F C、点D或点F D、点E或点G8. 如图,在矩形中, , , 对角线 , 相交于点O,点E,F分别是 , 的中点,连接 , 则的周长为( )
A、点D或点G B、点E或点F C、点D或点F D、点E或点G8. 如图,在矩形中, , , 对角线 , 相交于点O,点E,F分别是 , 的中点,连接 , 则的周长为( ) A、6 B、7 C、8 D、9
A、6 B、7 C、8 D、9二、填空题
-
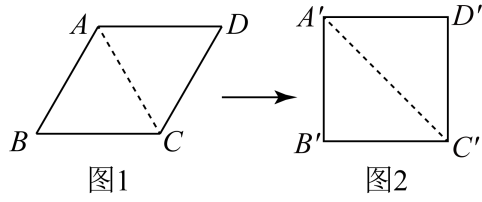
9. 若 则= .10. 关于x的一元二次方程有两个不相等的实数根,则a的取值范围是.11. 已知点 , 都在反比例函数的图象上,且 , 则和的大小关系为.12. 小颖将能够活动的菱形学具活动成为图1所示形状,并测得 , .接着,她又将这个学其活动成为图2所示正方形,此时的长为.
 13. 如图,在中, , 按以下步骤作图,①以点C为圆心,以适当的长为半径作弧,交于点D,交于点E,连接;②以点B为圆心,以长为半径作弧,交于点F;③以点F为圆心,以的长为半径作弧,在内与前一条弧相交于点G;④连接并延长交AC于点H,若H恰好为的中点,则的长为.
13. 如图,在中, , 按以下步骤作图,①以点C为圆心,以适当的长为半径作弧,交于点D,交于点E,连接;②以点B为圆心,以长为半径作弧,交于点F;③以点F为圆心,以的长为半径作弧,在内与前一条弧相交于点G;④连接并延长交AC于点H,若H恰好为的中点,则的长为. 14. 已知一元二次方程的两个根为 , 则的值为.15. 如图,矩形的对角线 , 相交于点O,过点O作 , 交于点E,若 , 则的大小为.
14. 已知一元二次方程的两个根为 , 则的值为.15. 如图,矩形的对角线 , 相交于点O,过点O作 , 交于点E,若 , 则的大小为.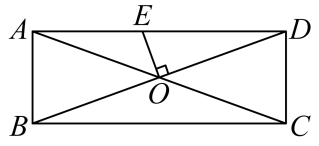 16. 如图,在平面直角坐标系中,的顶点A在函数的图象上,顶点B在x轴正半轴上,边 , 分别交的函数 , 的图象于点M,N.连接 , 若轴,则的面积为.
16. 如图,在平面直角坐标系中,的顶点A在函数的图象上,顶点B在x轴正半轴上,边 , 分别交的函数 , 的图象于点M,N.连接 , 若轴,则的面积为.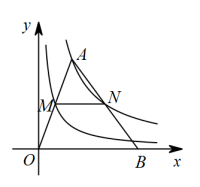
17. 如图,在矩形中, , , 点P是DC上一点,且 , 点E,F分别是上的动点,连接 , 始终满足.连接 , 记四边形的面积为 , 记的面积为 , 记的面积为 , 记的面积为 , 则.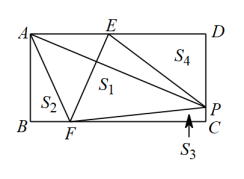 18. 如图,在平面直角坐标系中,正方形的顶点A,C的坐标分别为 , .已知线段的端点M,N的坐标分别为 , , 平移线段 , 使得平移后的线段的两个端点均落在正方形的边上,此时正方形被该线段分为两部分,其中三角形部分的面积为;已知线段的端点坐标分别为 , , 且 , , .平移线段 , 使得平移后的线段的两个端点均落在正方形的边上,且线段将正方形的面积分为两部分,取的中点H,连接 , 则的长为.
18. 如图,在平面直角坐标系中,正方形的顶点A,C的坐标分别为 , .已知线段的端点M,N的坐标分别为 , , 平移线段 , 使得平移后的线段的两个端点均落在正方形的边上,此时正方形被该线段分为两部分,其中三角形部分的面积为;已知线段的端点坐标分别为 , , 且 , , .平移线段 , 使得平移后的线段的两个端点均落在正方形的边上,且线段将正方形的面积分为两部分,取的中点H,连接 , 则的长为.
三、解答题
-
19.(1)、计算:;(2)、解方程:.20. 中国共产党第二十次全国代表大会于10月16日至22日在北京举行,这是一次具有里程碑意义的大会,必将对中国和世界产生深远影响.某校积极组织学生学习二十大相关会议精神,并组织了二十大知识问答赛,将比赛结果分为A,B,C,D四个等级,根据如下不完整的统计图解答下列问题:
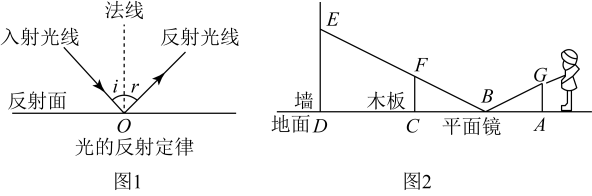
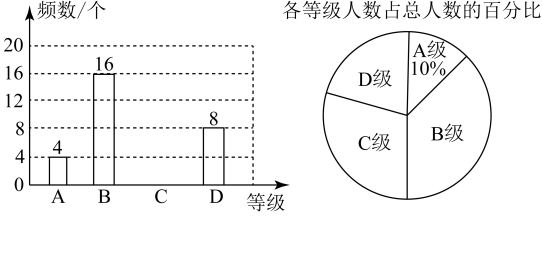 (1)、求该校参加知识问答赛的学生人数;(2)、求扇形统计图中C级所对应的圆心角的度数;(3)、现准备从结果为A级的4人(两男两女)中随机抽取两名同学参加二十大宣讲,请用列表或画树状图的方法,求恰好抽到一名男生和一名女生参加宣讲活动的概率.21. 【学科融合】如图1,在反射现象中,反射光线,入射光线和法线都在同一个平面内:反射光线和入射光线分别位于法线两例;入反射角r等于入射角i.这就是光的反射定律.
(1)、求该校参加知识问答赛的学生人数;(2)、求扇形统计图中C级所对应的圆心角的度数;(3)、现准备从结果为A级的4人(两男两女)中随机抽取两名同学参加二十大宣讲,请用列表或画树状图的方法,求恰好抽到一名男生和一名女生参加宣讲活动的概率.21. 【学科融合】如图1,在反射现象中,反射光线,入射光线和法线都在同一个平面内:反射光线和入射光线分别位于法线两例;入反射角r等于入射角i.这就是光的反射定律.【问题解决】如图2,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙,木板和平面镜,手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处,点E到地面的高度 , 点F到地面的高度 , 灯泡到木板的水平距离 , 木板到墙的水平距离为.图中A,B,C,D在同一条直线上.
 (1)、求的长;(2)、求灯泡到地面的高度.22. 如图1,的各内角的平分线分别相交于点E,F,G,H.
(1)、求的长;(2)、求灯泡到地面的高度.22. 如图1,的各内角的平分线分别相交于点E,F,G,H.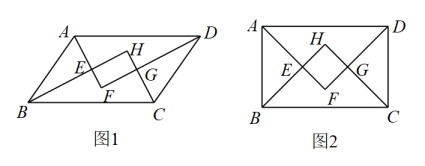 (1)、求证:四边形为矩形;(2)、如图2,当为矩形时,
(1)、求证:四边形为矩形;(2)、如图2,当为矩形时,①求证:四边形EFGH为正方形;
②若 , 四边形的面积为8,求AB的长.
23. 如图1,已知反比例函数的图象与一次函数的图象相交于A(2,a),B两点.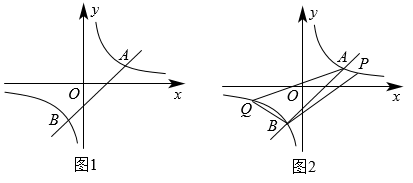 (1)、求反比例函数的表达式及A,B两点的坐标;(2)、M是x轴上一点,N是y轴上一点,若以A,B,M,N为顶点的四边形是以为边的平行四边形,求点M的坐标;(3)、如图2,反比例函数的图象上有P,Q两点,点P的横坐标为 , 点Q的横坐标与点P的横坐标互为相反数,连接 , , , .若的面积是的面积的3倍,求m的值.24. 电影《长津湖》是一部讲述抗美援朝题材影片,该片以朝鲜长津湖战役为背景,讲述一个志愿军连队在极寒严酷环境下坚守阵地奋勇杀敌、为战役胜利作出重要贡献的故事,2021年8月首映,深受人们的喜爱.2022年清明节来临之际某电影院开展“清明祭英烈共铸中华魂”系列活动,对团体购买该电影票实行优惠,决定在原定零售票价基础上每张降价元,这样按原定票价需花费元购买的门票张数,现在只花费了元.
(1)、求反比例函数的表达式及A,B两点的坐标;(2)、M是x轴上一点,N是y轴上一点,若以A,B,M,N为顶点的四边形是以为边的平行四边形,求点M的坐标;(3)、如图2,反比例函数的图象上有P,Q两点,点P的横坐标为 , 点Q的横坐标与点P的横坐标互为相反数,连接 , , , .若的面积是的面积的3倍,求m的值.24. 电影《长津湖》是一部讲述抗美援朝题材影片,该片以朝鲜长津湖战役为背景,讲述一个志愿军连队在极寒严酷环境下坚守阵地奋勇杀敌、为战役胜利作出重要贡献的故事,2021年8月首映,深受人们的喜爱.2022年清明节来临之际某电影院开展“清明祭英烈共铸中华魂”系列活动,对团体购买该电影票实行优惠,决定在原定零售票价基础上每张降价元,这样按原定票价需花费元购买的门票张数,现在只花费了元. (1)、求每张零售电影票的原定价;(2)、为了弘扬爱国主义精神,该影院决定对网上购票的个人也采取优惠,原定零售票价经过连续两次降价后票价为每张32.4元,求原定零售票价平均每次的下降率.25. 已知在平面直角坐标系中,点 , 在反比例函数的图象上.
(1)、求每张零售电影票的原定价;(2)、为了弘扬爱国主义精神,该影院决定对网上购票的个人也采取优惠,原定零售票价经过连续两次降价后票价为每张32.4元,求原定零售票价平均每次的下降率.25. 已知在平面直角坐标系中,点 , 在反比例函数的图象上.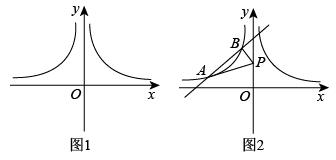 (1)、求k的值;(2)、将反比例函数的图象中x轴下方部分沿x轴翻折,其余部分保持不变,得到新的函数图象如图1所示,新函数记为函数F.
(1)、求k的值;(2)、将反比例函数的图象中x轴下方部分沿x轴翻折,其余部分保持不变,得到新的函数图象如图1所示,新函数记为函数F.①如图2,直线与函数F的图象交于A,B两点,点A横坐标为 , 点B横坐标为 , 且 , .点P在y轴上,连接AP,BP.当最小时,求点P的坐标;
②已知一次函数)的图象与函数F的图象有三个不同的交点,直接写出n的取值范围.
26. 【问题背景】如图1,在矩形中,点M,N分别在边 , 上,且 , 连接 , 点P在上,连接并延长至点Q,使 , 连接.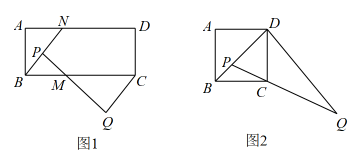 (1)、【尝试初探】求证:;(2)、【深入探究】若 , , 点P为中点,连接 , , 求证:;(3)、【拓展延伸】如图2,在正方形中,点P为对角线上一点,连接并延长至点Q,使 , 连接 , 若 , 求的值(用含n的代数式表示)
(1)、【尝试初探】求证:;(2)、【深入探究】若 , , 点P为中点,连接 , , 求证:;(3)、【拓展延伸】如图2,在正方形中,点P为对角线上一点,连接并延长至点Q,使 , 连接 , 若 , 求的值(用含n的代数式表示)