浙江省宁波市2023年初中学业水平模拟考试数学试题

试卷更新日期：2023-03-15 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，属于负数的是（）

A、8 B、5.6 C、 $- \frac{2}{3}$ D、 $\frac{1}{2}$

查看试题解析
2. $- [a - (b + c)]$ 去括号后应为（）

A、 $- a - b + c$ B、 $- a + b - c$ C、 $- a - b - c$ D、 $- a + b + c$

查看试题解析
3. 第四届世界茉莉花大会、2022年中国（横州）茉莉花文化节于9月19日、20日在南宁市和横州市两地举行，茉莉花产业成了横州市一张靓丽的名片，目前横州市茉莉花种植面积约125000亩.数据125000用科学记数法可表示为（）

A、 $0.125 \times 1 0^{6}$ B、 $1.25 \times 1 0^{5}$ C、 $12.5 \times 1 0^{4}$ D、 $125 \times 1 0^{3}$

查看试题解析
4. 如图所示的手提水果篮，其俯视图是（）

A、 B、 C、 D、

查看试题解析
5. 为庆祝2022年11月29日神舟十五号载人飞船发射成功，学校开展航天知识竞赛活动.经过几轮筛选，九（1）班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛，经过统计，四名同学成绩的平均数（单位：分）及方差（单位：分²）如表所示：

甲
乙
丙
丁
平均数
97
96
98
98
方差
1.6
0.3
0.3
1.8
如果要选一名成绩好且状态稳定的同学参赛，那么应该选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 分式 $\frac{1}{x - 3}$ 有意义，则 $x$ 的取值范围是（）

A、 $x > 3$ B、 $x < 3$ C、 $x \neq 3$ D、 $x \neq - 3$

查看试题解析
7. 如图， $E F$ 是 $△ A B C$ 的中位线， $B D$ 平分 $∠ A B C$ 交 $E F$ 于点D，若 $A E = 3$ ， $D F = 1$ ，则边 $B C$ 的长为（）

A、7 B、8 C、9 D、10

查看试题解析
8. 某活动小组购买了4个篮球和5个足球，一共花费435元，其中篮球的单价比足球的单价多3元，求篮球的单价和足球的单价.设篮球的单价为 $x$ 元，足球的单价为 $y$ 元，依题意可列方程组为（）

A、 ${\begin{array}{l} x - y = 3 \\ 4 y + 3 y = 435 \end{array}$ B、 ${\begin{array}{l} y - x = 3 \\ 4 x + 5 y = 435 \end{array}$ C、 ${\begin{array}{l} x = 3 - y \\ 4 x + 5 y = 435 \end{array}$ D、 ${\begin{array}{l} x - y = 3 \\ 4 x + 5 y = 435 \end{array}$

查看试题解析
9. 如图，一次函数 $y = a x + b$ 与反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象交于点 $A (1 ， 2)$ ， $B (m ， - 1)$ .则关于x的不等式 $a x + b > \frac{k}{x}$ 的解集是（）

A、 $x < - 2$ 或 $0 < x < 1$ B、 $x < - 1$ 或 $0 < x < 2$ C、 $- 2 < x < 0$ 或 $x > 1$ D、 $- 1 < x < 0$ 或 $x > 2$

查看试题解析
10. 如图是一个由A、B、C三种相似的直角三角形纸片拼成的矩形，A、B、C的纸片的面积分别为S₁、S₂、S₃ ，（S₁与S₂ ， S₂与S₃的相似比相同），相邻纸片之间互不重叠也无缝隙，若S₁＞S₂＞S₃ ，则这个矩形的面积一定可以表示为（）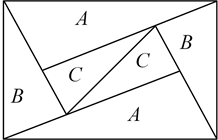

A、4S₁ B、6S₂ C、4S₂+3S₃ D、3S₁+4S₃

查看试题解析

二、填空题

11. $π - 4$ 的绝对值是．

查看试题解析
12. 因式分解： $x^{2} + 3 x + 1 =$ .

查看试题解析
13. 国庆节期间，小红的妈妈经营的玩具店进了一纸箱除颜色外都相同的散装塑料球共 1000个，小红将纸箱里面的球搅匀后，从中随机摸出一个球记下其颜色，把它放回纸箱中；搅匀后再随机摸出一个球记下其颜色，把它放回纸箱中；…多次重复上述过程后，发现摸到红球的频率逐渐稳定在0.3，由此可以估计纸箱内红球的个数约是个．

查看试题解析
14. 如图 $A B 、 A C 、 B D$ 是圆O的切线，切点分别为P、C、D，若 $A B = 5$ ， $B D = 2$ ，则 $A C$ 的长是.

查看试题解析
15. 如图，菱形 $O A B C$ 的一边 $O A$ 在 $x$ 轴的负半轴上，O是坐标原点，A点坐标为 $(- 5 ， 0)$ ，对角线 $A C$ 和 $O B$ 相交于点D且 $A C \cdot O B = 40$ .若反比例函数 $y = \frac{k}{x} (x < 0)$ 的图象经过点D，并与 $B C$ 的延长线交于点E，则 $S_{△ O C E} =$ .

查看试题解析
16. 如图，在矩形纸片 $A B C D$ 中， $A B = 12$ ， $A D = 4$ ，按以下步骤操作：
第一步，在边 $A B$ 上取一点 $M$ ，且满足 $B M = 2 B C$ ，现折叠纸片，使点 $C$ 与点 $M$ 重合，点 $B$ 的对应点为点 $B^{'}$ ，则得到的第一条折痕 $E F$ 的长为.
第二步，继续折叠纸片，使得到的第二条折痕与 $E F$ 垂直，点 $D$ 的对应点为 $D^{'}$ ，则点 $B^{'}$ 和点 $D^{'}$ 之间的最小距离为.

查看试题解析

三、解答题

17. 计算：

(1)、 $- 2 + 3 - (- 5) + 7$ ；

(2)、 $- 1^{2021} + | - 7 | - \sqrt{9} + 5 \div \frac{1}{2} \times 2 - \sqrt[3]{8}$ .

查看试题解析
18. 作图题

(1)、填空：如果长方形的长为3，宽为2，那么对角线的长为.

(2)、如图，正方形网格中的每个小正方形边长都为1，每个小正方形的顶点叫格点，以格点为顶点（端点），分别按下列要求画图（不要求写画法和证明，但要标注顶点）.
①在图1中，画一个面积为4的菱形，且邻边不垂直.
②在图2中，画 $▱ A B C D$ ，使 $∠ A = 45 °$ ，且面积为6.

查看试题解析
19. 已知抛物线 $y = a x^{2} + b x + 5$ 经过点 $(1 ， 0)$ ， $(- 1 ， 12)$ .

(1)、求该二次函数的解析式；

(2)、用配方法将（1）中的解析式化为顶点式 $y = a {(x - h)}^{2} + k$ 的形式，并写出顶点坐标

查看试题解析
20. 某校举行“汉字听写”比赛，每位学生听写39个汉字，比赛结束后随机抽查部分学生的听写结果，以下是根据抽查结果绘制的统计图表的一部分，请根据统计图表的信息解决下列问题，
组别正确字数x人数
$A$
$0 ≤ x < 8$
10
$B$
$8 \leq x < 16$
15
$C$
$16 ≤ x < 24$
25
$D$
$24 ≤ x < 32$
$m$
$E$
$32 ≤ x < 40$
$n$

(1)、在统计表中， $m =$ ▲ ， $n =$ ▲ ，并补全直方图；

(2)、在扇形统计图中“ $C$ 组”所对应的圆心角的度数是；

(3)、若该校共有2000名学生，如果听写正确的个数不少于32个定为“优秀”，请你估算这所学校本次比赛听写“优秀”的学生人数.

查看试题解析
21. 我国南北朝数学家祖冲之研制了水碓磨-利用水力舂米的器械．《天工开物》中绘有一个水轮带动四个碓的画面，如图1．碓杆 $A B$ 的简意图如图2， $O M$ 是垂直水平地面的支柱， $A B = 8$ 米， $O A ： O B = 1 ： 3$ ．当点A位于最低点时， $∠ A O M = 6 0^{∘}$ ；当点A位于最高点 $A^{'}$ 时， $∠ A^{'} O M = 108 . 2^{∘}$ ．过点O作直线 $E F$ 垂直于 $O M$ ，分别过点B， $B^{'}$ 作 $B C ⊥ E F$ ， $B^{'} D ⊥ E F$ ，垂足分别为C，D．

(1)、求 $∠ B O D$ 和 $∠ B^{'} O D$ 的度数；

(2)、求点B从最高点到最低点 $B^{'}$ 之间的垂直距离（即求 $B C + B^{'} D$ 的长）．（参考数据： $s i n 18 . 2^{∘} \approx 0.31$ ， $c o s 18 . 2^{∘} \approx 0.95$ ， $t a n 18 . 2^{∘} \approx 0.33$ ）

查看试题解析
22. 小李、小王分别从甲地出发，骑自行车沿同一条路到乙地参加公益活动.如图，折线 $O A B$ 和线段 $C D$ 分别表示小李、小王离甲地的距离y（单位：千米）与时间x（单位：小时）之间的函数关系.根据图中提供的信息，解答下列问题：

(1)、求小王的骑车速度，点C的横坐标；

(2)、求线段 $A B$ 对应的函数表达式；

(3)、当小王到达乙地时，小李距乙地还有多远？

查看试题解析
23. 如图

(1)、【证明体验】如图1，正方形 $A B C D$ 中，E、F分别是边 $A B$ 和对角线 $A C$ 上的点， $∠ E D F = 45 °$ .
①求证： $△ D B E ∼ △ D C F$ ；
② $\frac{B E}{C F} =$ ▲ ；

(2)、【思考探究】如图2，矩形 $A B C D$ 中， $A B = 6$ ， $B C = 8$ ， E、F分别是边 $A B$ 和对角线 $A C$ 上的点， $t a n ∠ E D F = \frac{4}{3}$ ， $B E = 5$ ，求 $C F$ 的长；

(3)、【拓展延伸】如图3，菱形 $A B C D$ 中， $B C = 5$ ，对角线 $A C = 6$ ， $B H ⊥ A D$ 交 $D A$ 的延长线于点H，E、F分别是线段 $H B$ 和 $A C$ 上的点， $t a n ∠ E D F = \frac{3}{4}$ ， $H E = \frac{8}{5}$ ，求 $C F$ 的长.

查看试题解析
24. 如图 $1$ ，已知 $A B$ 为 $⊙ O$ 的直径，点 $C$ 为 $\overset{⌢}{A B}$ 的中点，点 $D$ 在 $\overset{⌢}{B C}$ 上，连接 $B D$ 、 $C D$ 、 $B C$ 、 $A D$ 、 $B C$ 与 $A D$ 相交于点 $E$ .

(1)、求证： $∠ C + ∠ C B D = ∠ C B A$ ；

(2)、如图2，过点C作 $C D$ 的垂线，分别与 $A D$ ， $A B$ ， $⊙ O$ 相交于点F、G、H，求证： $A F = B D$ ；

(3)、如图3，在（2）的条件下，连接 $B F$ ，若 $B F = B C$ ， $△ C E F$ 的面积等于3，求 $F G$ 的长.

查看试题解析

$A$	$0 ≤ x < 8$	10
$B$	$8 \leq x < 16$	15
$C$	$16 ≤ x < 24$	25
$D$	$24 ≤ x < 32$	$m$
$E$	$32 ≤ x < 40$	$n$

	甲	乙	丙	丁
平均数	97	96	98	98
方差	1.6	0.3	0.3	1.8