陕西省西安市莲湖区2023年中考数学第一次模拟考试数学试题
试卷更新日期:2023-03-15 类型:中考模拟
一、单选题
-
1. 如图,在数轴上,点、分别表示数、 , 且.若、两点间的距离为6,则点表示的数为( )
 A、-6 B、6 C、-3 D、32. 下列命题:①若 , 则;②同旁内角互补,两直线平行;③相等的角是对顶角;④无限小数是无理数.其中假命题的是( )A、①② B、②③ C、②③④ D、①③④3. 计算正确的是( )A、 B、 C、 D、4. 如图,平行四边形ABCD中,对角线AC、BD相交于点O,则下列结论中不正确的是( )
A、-6 B、6 C、-3 D、32. 下列命题:①若 , 则;②同旁内角互补,两直线平行;③相等的角是对顶角;④无限小数是无理数.其中假命题的是( )A、①② B、②③ C、②③④ D、①③④3. 计算正确的是( )A、 B、 C、 D、4. 如图,平行四边形ABCD中,对角线AC、BD相交于点O,则下列结论中不正确的是( ) A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当AC=BD时,它是矩形 D、当AC垂直平分BD时,它是正方形5. 在同一平面直角坐标系中,直线与相交于点 , 则关于x,y的方程组的解为( )A、 B、 C、 D、6. 如图,的顶点均在上,连接 , , 若 , 则的度数是( )
A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当AC=BD时,它是矩形 D、当AC垂直平分BD时,它是正方形5. 在同一平面直角坐标系中,直线与相交于点 , 则关于x,y的方程组的解为( )A、 B、 C、 D、6. 如图,的顶点均在上,连接 , , 若 , 则的度数是( )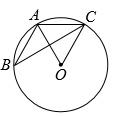 A、 B、 C、 D、7. 已知抛物线 , 下列说法正确的是( )A、抛物线的开口方向向下 B、抛物线的对称轴是直线 C、抛物线与轴交于点 D、抛物线与轴没有交点
A、 B、 C、 D、7. 已知抛物线 , 下列说法正确的是( )A、抛物线的开口方向向下 B、抛物线的对称轴是直线 C、抛物线与轴交于点 D、抛物线与轴没有交点二、填空题
-
8. 的大小顺序是(用“>”号连接).9. 若代数式:的值等于 , 则的值等于.10. 比较大小:1.(填“”“ ”或“”)11. 五角星是我们生活中常见的一种图形,如图,C,D为线段AB的黄金分割点,AB=2,则五边形CDEFG的周长为.
 12. 若关于x的一元二次方程有一个根是1,则m的值为 .13. 如图,在菱形中,对角线交于O,且对角线 , , 点E是边的中点,则.
12. 若关于x的一元二次方程有一个根是1,则m的值为 .13. 如图,在菱形中,对角线交于O,且对角线 , , 点E是边的中点,则.
三、解答题
-
14. 计算:15. 解不等式组16. 计算:(1)、(2)、17. 如图所示, , , , 是上两点,且.
 (1)、试说明;(2)、请你判断与的位置关系,并说明理由.18. 如图,在四边形ABCD中,AB∥CD,连接BD,点E在BD上,连接CE,若∠1=∠2,AB=ED,求证:DB=CD.
(1)、试说明;(2)、请你判断与的位置关系,并说明理由.18. 如图,在四边形ABCD中,AB∥CD,连接BD,点E在BD上,连接CE,若∠1=∠2,AB=ED,求证:DB=CD.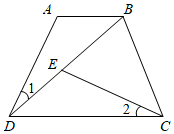 19. 如图,一次函数的图象和y轴交于点B,与正比例函数图象交于点P.
19. 如图,一次函数的图象和y轴交于点B,与正比例函数图象交于点P. (1)、求m和n的值;(2)、求的面积.20. 作为中国共产党建党百年的献礼,我校精心策划“庆祝中国共产党成立100周年”歌唱比赛,歌曲有:《没有共产党就没有新中国》,《歌唱祖国》,《少年中国说》(分别用字母 , , 依次表示这三首歌曲)比赛时,将 , , 这三个字母分别写在张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,九年一班班长先从中随机抽取一张卡片,放回后洗匀,再由九年二班班长从中随机抽取一张卡片,进行歌唱比赛.(1)、九年一班抽中歌曲《少年中国说》的概率是;(2)、试用画树状图或列表的方法表示所有可能的结果,并求出一班和二班抽中不同歌曲的概率.21. 为测量一棵大树的高度,设计的测量方案如图所示:标杆高度 , 人的眼睛A、标杆的顶端C和大树顶端M在一条直线上,标杆与大树的水平距离 , 人的眼睛与地面的高度 , 人与标杆的水平距离 , B、D、N三点共线, , 求大树的高度.
(1)、求m和n的值;(2)、求的面积.20. 作为中国共产党建党百年的献礼,我校精心策划“庆祝中国共产党成立100周年”歌唱比赛,歌曲有:《没有共产党就没有新中国》,《歌唱祖国》,《少年中国说》(分别用字母 , , 依次表示这三首歌曲)比赛时,将 , , 这三个字母分别写在张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,九年一班班长先从中随机抽取一张卡片,放回后洗匀,再由九年二班班长从中随机抽取一张卡片,进行歌唱比赛.(1)、九年一班抽中歌曲《少年中国说》的概率是;(2)、试用画树状图或列表的方法表示所有可能的结果,并求出一班和二班抽中不同歌曲的概率.21. 为测量一棵大树的高度,设计的测量方案如图所示:标杆高度 , 人的眼睛A、标杆的顶端C和大树顶端M在一条直线上,标杆与大树的水平距离 , 人的眼睛与地面的高度 , 人与标杆的水平距离 , B、D、N三点共线, , 求大树的高度.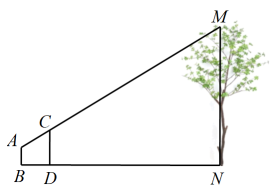 22. 如图1,小明家、食堂、图书馆在同一条直线上,小明从食堂吃完早餐,接着骑自行车去图书馆读书,然后以相同的速度原路返回家.如图2中反映了小明离家的距离与他所用时间之间的函数关系.
22. 如图1,小明家、食堂、图书馆在同一条直线上,小明从食堂吃完早餐,接着骑自行车去图书馆读书,然后以相同的速度原路返回家.如图2中反映了小明离家的距离与他所用时间之间的函数关系.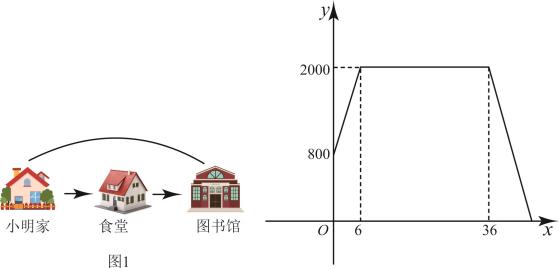 (1)、小明家与图书馆的距离为 , 小明骑自行车速度为;(2)、求小明从图书馆返回家的过程中,与的函数解析式;(3)、当小明离家的距离为时,求的值.23. 国家规定:中小学生每天在校体育活动时间不少于.为此,某市就“每天在校体育活动时间”的问题随机调查了辖区内部分初中学生,根据调查结果绘制成的统计图(部分)如图所示(组:;组:;组:;组:).请根据上述信息解答下列问题:
(1)、小明家与图书馆的距离为 , 小明骑自行车速度为;(2)、求小明从图书馆返回家的过程中,与的函数解析式;(3)、当小明离家的距离为时,求的值.23. 国家规定:中小学生每天在校体育活动时间不少于.为此,某市就“每天在校体育活动时间”的问题随机调查了辖区内部分初中学生,根据调查结果绘制成的统计图(部分)如图所示(组:;组:;组:;组:).请根据上述信息解答下列问题: (1)、本次调查的人数为 , 组对应扇形的圆心角度数为;(2)、请补全频数分布直方图:(3)、若该市约有80000名初中生,请估计其中达到国家珵定的体育活动时间的学生人数.24. 如图,是⊙的直径,是⊙的切线,、是⊙的弦,且 , 垂足为E,连接并延长,交于点P.
(1)、本次调查的人数为 , 组对应扇形的圆心角度数为;(2)、请补全频数分布直方图:(3)、若该市约有80000名初中生,请估计其中达到国家珵定的体育活动时间的学生人数.24. 如图,是⊙的直径,是⊙的切线,、是⊙的弦,且 , 垂足为E,连接并延长,交于点P.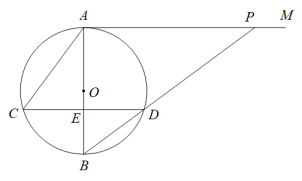 (1)、求证:;(2)、若⊙的半径 , 求线段的长.
(1)、求证:;(2)、若⊙的半径 , 求线段的长.

