陕西省西安市雁塔区2023年中考数学第一次模拟考试卷
试卷更新日期:2023-03-15 类型:中考模拟
一、单选题
-
1. 2.5的相反数是( )A、2.5 B、-2.5 C、 D、2. 如图, AB∥CD,射线交于点 , , 则的度数是( )
 A、50° B、60° C、70° D、80°3. 下列计算错误的是( )A、 B、 C、 D、4. 如图,四边形ABCD的对角线互相平分,要使它成为矩形,那么需要添加的条件是( )
A、50° B、60° C、70° D、80°3. 下列计算错误的是( )A、 B、 C、 D、4. 如图,四边形ABCD的对角线互相平分,要使它成为矩形,那么需要添加的条件是( ) A、AB=BC B、AC垂直BD C、∠A=∠C D、AC=BD5. 如图,在中,为斜边上的中线,过点D作 , 连接 , 若 , , 则的长为( )
A、AB=BC B、AC垂直BD C、∠A=∠C D、AC=BD5. 如图,在中,为斜边上的中线,过点D作 , 连接 , 若 , , 则的长为( )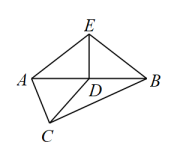 A、2 B、3 C、4 D、56. 如图,是在同一坐标系内作出的一次函数、的图象,设 , , 则方程组的解是( )
A、2 B、3 C、4 D、56. 如图,是在同一坐标系内作出的一次函数、的图象,设 , , 则方程组的解是( )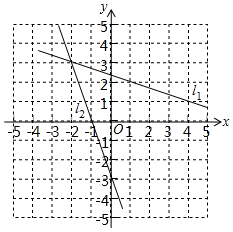 A、 B、 C、 D、7. 如图,的顶点均在上,连接 , , 若 , 则的度数是( )
A、 B、 C、 D、7. 如图,的顶点均在上,连接 , , 若 , 则的度数是( )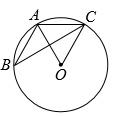 A、 B、 C、 D、8. 对于二次函数的图象,下列说法正确的是( )A、图象与y轴交点的坐标是 B、对称轴是直线 C、顶点坐标为 D、当时,y随x的增大而增大
A、 B、 C、 D、8. 对于二次函数的图象,下列说法正确的是( )A、图象与y轴交点的坐标是 B、对称轴是直线 C、顶点坐标为 D、当时,y随x的增大而增大二、填空题
-
9. 计算:.10. 比较大小.(填或)11. 如图,点P把线段的黄金分割点,且.如果 , 那么(结果保留一位小数).
 12. 如图1,在菱形ABCD中,∠BAD=60°,点E在AB的延长线上,在∠CBE的角平分线上取一点F(含端点B),连接AF并过点C作AF所在直线的垂线,垂足为G.设线段AF的长为x,CG的长为y,y关于x的函数图象及有关数据如图2所示,点Q为图象的端点,则时,BF=.
12. 如图1,在菱形ABCD中,∠BAD=60°,点E在AB的延长线上,在∠CBE的角平分线上取一点F(含端点B),连接AF并过点C作AF所在直线的垂线,垂足为G.设线段AF的长为x,CG的长为y,y关于x的函数图象及有关数据如图2所示,点Q为图象的端点,则时,BF=.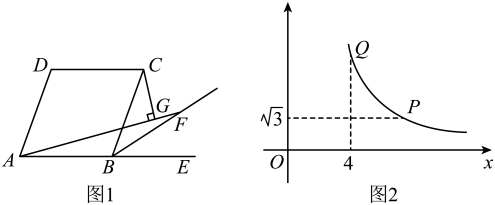 13. 如图,在菱形中,点、分别是、的中点,连接交对角线于点 , 连接若 , , 则的长为 .
13. 如图,在菱形中,点、分别是、的中点,连接交对角线于点 , 连接若 , , 则的长为 .
三、解答题
-
14. 计算(1)、(2)、15. 解不等式组并把解集在数轴上表示出来.16.(1)、化简:;(2)、先化简,再求值: , 其中x=2022.17. 如图,在中, , 将绕点B逆时针旋转到的延长线与相交于点F,连接 , 求证:.
 18. 已知, , , 求证: .
18. 已知, , , 求证: .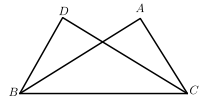 19. 如图所示,在平面直角坐标系中,已知、、;
19. 如图所示,在平面直角坐标系中,已知、、; (1)、若点与点关于轴对称,则点的坐标为;(2)、在平面直角坐标系中画出关于轴对称的图形;(3)、已知为y轴上一点,若的面积为2,直接写出点的坐标.20. 电影公司随机收集了电影的有关数据,经分类整理得到下表:
(1)、若点与点关于轴对称,则点的坐标为;(2)、在平面直角坐标系中画出关于轴对称的图形;(3)、已知为y轴上一点,若的面积为2,直接写出点的坐标.20. 电影公司随机收集了电影的有关数据,经分类整理得到下表:电影类型
第一类
第二类
第三类
第四类
第五类
第六类
电影部数
140
50
300
200
800
510
好评率
0.4
0.2
0.25
0.2
0.1
说明:好评率是指一类电影中获得好评的部数与该类电影的部数的比值.
(1)、已知第三类电影获得好评的有45部,则;(2)、如果电影公司从收集的电影中随机选取1部,求抽到的这部电影是第四类电影中的好评电影的概率;(3)、根据前期调查反馈:第一类电影上座率与好评率的关系约为:上座率=好评率×1.5+0.1,第二类电影上座率与好评率的关系约为:上座率=好评率×1.5+0.1.现有一部第一类的A电影和一部第二类的B电影将同时在某影院上映.A电影的票价为45元,B电影的票价为40元,该影院的最大放映厅的满座人数为1000人,公司要求排片经理将这两部电影安排在最大放映厅放映,且两部电影每天都要有排片.现有3个场次可供排片,仅从该放映厅的票房收入最高考虑,排片经理应如何分配A、B两部电影的场次,以使得当天的票房收入最高?21. 为测量一棵大树的高度,设计的测量方案如图所示:标杆高度 , 人的眼睛A、标杆的顶端C和大树顶端M在一条直线上,标杆与大树的水平距离 , 人的眼睛与地面的高度 , 人与标杆的水平距离 , B、D、N三点共线, , 求大树的高度.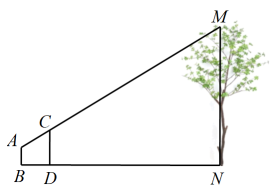 22. 明明在计算机中设计了一个有理数运算的程序:;当输入 , 的数据时,屏幕会根据运算程序显示出结果.(1)、求的值;(2)、芳芳在运用这个程序计算时,输入 , 的数据后屏幕显示“操作无法进行”,请你猜想芳芳输入数据时可能出现了什么情况,为什么?23. 某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生听写结果,图1,图2是根据抽查结果绘制的统计图的一部分.
22. 明明在计算机中设计了一个有理数运算的程序:;当输入 , 的数据时,屏幕会根据运算程序显示出结果.(1)、求的值;(2)、芳芳在运用这个程序计算时,输入 , 的数据后屏幕显示“操作无法进行”,请你猜想芳芳输入数据时可能出现了什么情况,为什么?23. 某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生听写结果,图1,图2是根据抽查结果绘制的统计图的一部分.组别
听写正确的个数x
人数
10
15
25

根据以上信息解决下列问题:
(1)、本次共随机抽查了多少名学生,并补全图2的条形统计图;(2)、求出图1中的度数;(3)、该校共有3000名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.24. 如图①,在中, , 是的中点,为内一点,连接并延长到 , 使得 , 连接.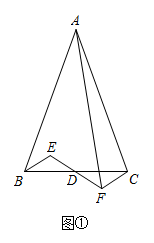 (1)、求证:;(2)、若 , 求证:;(3)、如图②,探索当与满足什么数量关系时, , 并说明理由.
(1)、求证:;(2)、若 , 求证:;(3)、如图②,探索当与满足什么数量关系时, , 并说明理由.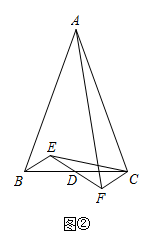 25. 漪汾桥是太原市首座对称双七拱吊桥,每个桥拱呈大小相等的抛物线型,桥拱如长虹出水,屹立于汾河之上,是太原市地标性建筑之一.如图2所示,单个桥拱在桥面上的跨度OA=60米,在水面的跨度BC=80米,桥面距水面的垂直距离OE=7米,以桥面所在水平线为x轴,OE所在直线为y轴建立平面直角坐标系.
25. 漪汾桥是太原市首座对称双七拱吊桥,每个桥拱呈大小相等的抛物线型,桥拱如长虹出水,屹立于汾河之上,是太原市地标性建筑之一.如图2所示,单个桥拱在桥面上的跨度OA=60米,在水面的跨度BC=80米,桥面距水面的垂直距离OE=7米,以桥面所在水平线为x轴,OE所在直线为y轴建立平面直角坐标系. (1)、求桥拱所在抛物线的函数关系表达式;(2)、求桥拱最高点到水面的距离是多少米?26. 如图,在中, , , , 点D是斜边上的动点,连接 , 垂直平分交射线于点F,交边于点E.
(1)、求桥拱所在抛物线的函数关系表达式;(2)、求桥拱最高点到水面的距离是多少米?26. 如图,在中, , , , 点D是斜边上的动点,连接 , 垂直平分交射线于点F,交边于点E. (1)、如图,当点D是斜边上的中点时,求的长;(2)、连接 , 如果和相似,求的长;(3)、当点F在边的延长线上,且时,求的长.
(1)、如图,当点D是斜边上的中点时,求的长;(2)、连接 , 如果和相似,求的长;(3)、当点F在边的延长线上,且时,求的长.