陕西省宝鸡市2023年中考数学第一次模拟考试卷
试卷更新日期:2023-03-15 类型:中考模拟
一、单选题
-
1. -2的相反数为( )A、0 B、-1 C、2 D、12. 如图,直线相交于点O, , 若 , 则的度数为( )
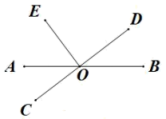 A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,平行四边形ABCD中,对角线AC、BD相交于点O,则下列结论中不正确的是( )
A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,平行四边形ABCD中,对角线AC、BD相交于点O,则下列结论中不正确的是( ) A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当AC=BD时,它是矩形 D、当AC垂直平分BD时,它是正方形5. 如图,∠AOB=90°,OA=25m,OB=5m,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球,如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是( ).
A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当AC=BD时,它是矩形 D、当AC垂直平分BD时,它是正方形5. 如图,∠AOB=90°,OA=25m,OB=5m,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球,如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是( ).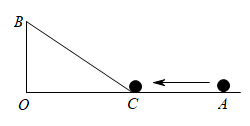 A、12米 B、13米 C、14米 D、15米6. 如果直线与交点坐标为 , 则解为的方程组是( )A、 B、 C、 D、7. 已知等腰中, , 则的度数为( )A、 B、 C、或 D、或或8. 已知二次函数y=x2−2x−3的自变量x1 , x2 , x3对应的函数值分别为y1 , y2 , y3.当−1<x1<0,1<x2<2,x3>3时,y1 , y2 , y3三者之间的大小关系是( )A、 B、 C、 D、
A、12米 B、13米 C、14米 D、15米6. 如果直线与交点坐标为 , 则解为的方程组是( )A、 B、 C、 D、7. 已知等腰中, , 则的度数为( )A、 B、 C、或 D、或或8. 已知二次函数y=x2−2x−3的自变量x1 , x2 , x3对应的函数值分别为y1 , y2 , y3.当−1<x1<0,1<x2<2,x3>3时,y1 , y2 , y3三者之间的大小关系是( )A、 B、 C、 D、二、填空题
-
9. 计算:=10. 比较大小:1.(填“”“ ”或“”)11. 在矩形内作正方形(如图所示),矩形的对角线交正方形的边于点P.如果点F恰好是边的黄金分割点 , 且 , 那么.
 12. 如图,过反比例函数的图象上一点A作轴于点B,连接 , 若 , 则k的值为.
12. 如图,过反比例函数的图象上一点A作轴于点B,连接 , 若 , 则k的值为. 13. 如图,在菱形中,点、分别是、的中点,连接交对角线于点 , 连接若 , , 则的长为 .
13. 如图,在菱形中,点、分别是、的中点,连接交对角线于点 , 连接若 , , 则的长为 .
三、解答题
-
14. 计算:15. 解不等式组16. 计算:(1)、(2)、17. 如图, , , , 在同一条直线上,于点 , 于点 , , , 求证:.
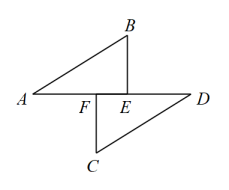 18. 已知:如图,在菱形中,E.F分别是边和上的点,且 , 求证:.
18. 已知:如图,在菱形中,E.F分别是边和上的点,且 , 求证:. 19. 如图,在平面直角坐标系中,已知的三个顶点坐标分别是.
19. 如图,在平面直角坐标系中,已知的三个顶点坐标分别是. (1)、画出关于y轴的对称图形(2)、画出关于x轴的对称图形(3)、的面积为.20. 有五个封装后外观完全相同的纸箱,且每个纸箱内各装有一个西瓜,其中,所装西瓜的重量分别为6kg,6kg,7kg,7kg,8kg.现将这五个纸箱随机摆放.(1)、若从这五个纸箱中随机选1个,则所选纸箱里西瓜的重量为6kg的概率是;(2)、若从这五个纸箱中随机选2个,请利用列表或画树状图的方法,求所选两个纸箱里西瓜的重量之和为15kg的概率.21. 小明和小华利用学过的知识测量操场旗杆的高度,测量时,小明让小华站在点B处,此时,小华影子的顶端E与旗杆的影子C顶端重合,且的长为2米;小明又让小华沿着射线的方向走15.2米到达旗杆的另一侧N处,此时,小华观测到旗杆顶端C的仰角为 , 已知小华的身高为1.8米,请你根据相关测量信息,计算旗杆的高度.
(1)、画出关于y轴的对称图形(2)、画出关于x轴的对称图形(3)、的面积为.20. 有五个封装后外观完全相同的纸箱,且每个纸箱内各装有一个西瓜,其中,所装西瓜的重量分别为6kg,6kg,7kg,7kg,8kg.现将这五个纸箱随机摆放.(1)、若从这五个纸箱中随机选1个,则所选纸箱里西瓜的重量为6kg的概率是;(2)、若从这五个纸箱中随机选2个,请利用列表或画树状图的方法,求所选两个纸箱里西瓜的重量之和为15kg的概率.21. 小明和小华利用学过的知识测量操场旗杆的高度,测量时,小明让小华站在点B处,此时,小华影子的顶端E与旗杆的影子C顶端重合,且的长为2米;小明又让小华沿着射线的方向走15.2米到达旗杆的另一侧N处,此时,小华观测到旗杆顶端C的仰角为 , 已知小华的身高为1.8米,请你根据相关测量信息,计算旗杆的高度. 22. 在学习代数式的值时,介绍了计算框图:用“
22. 在学习代数式的值时,介绍了计算框图:用“ ”表示数据输入、输出框;用“
”表示数据输入、输出框;用“  ”表示数据处理和运算框;用“
”表示数据处理和运算框;用“  ”表示数据判断框(根据条件决定执行两条路径中的某一条)
”表示数据判断框(根据条件决定执行两条路径中的某一条)  (1)、①如图1,当输入数 时,输出数 ;
(1)、①如图1,当输入数 时,输出数 ;②如图2,第一个带?号的运算框内,应填;第二个带?号运算框内,应填;
(2)、①如图3,当输入数 时,输出数 ;②如图4,当输出的值 ,则输入的值 ;
(3)、为鼓励节约用水,决定对用水实行“阶梯价”:当每月用水量不超过15吨时(含15吨),以2元/吨的价格收费;当每月用水量超过15吨时,超过部分以3元/吨的价格收费.请设计出一个“计算框图”,使得输入数为用水量 ,输出数为水费 .23. 2022年3月25日,教育部印发《义务教育课程方案和课程标准(2022年版)》,优化了课程设置,将劳动从综合实践活动课程中独立出来.某校为了解该校学生一周的课外劳动情况,随机抽取部分学生调查了他们一周的课外劳动时间,将数据进行整理并制成如下统计图.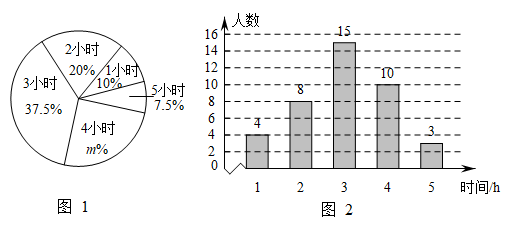
请根据图中提供的信息,解答下面的问题:
(1)、求图1中的m= , 本次调查数据的中位数是h,本次调查数据的众数是h;(2)、该校此次抽查的这些学生一周平均的课外劳动时间是多少?(3)、若该校共有2000名学生,请根据统计数据,估计该校学生一周的课外劳动时间不小于的人数.24. 在中, , , 是的角平分线. (1)、如图1,点E、F分别是线段、上的点,且 , 与的延长线交于点G,则与的数量关系是 , 位置关系是;(2)、如图2,点E、F分别在和的延长线上,且 , 的延长线交于点G.
(1)、如图1,点E、F分别是线段、上的点,且 , 与的延长线交于点G,则与的数量关系是 , 位置关系是;(2)、如图2,点E、F分别在和的延长线上,且 , 的延长线交于点G.①(1)中的结论还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
②连接 , 若 , , 求的长.
25. 对于向上抛的物体,如果空气阻力忽略不计,有下面的关系式:(是物体离起点的高度,是初速度,是重力系数,取 , 是抛出后经过的时间).杂技演员抛球表演时,以的初速度把球向上拋出.(1)、球抛出后经多少秒回到起点?(2)、几秒后球离起点的高度达到?(3)、球离起点的高度能达到吗?请说明理由.26. 在等边△ABC中,点D是直线BC上的一个点(不与点B、C重合),以AD为边在AD右侧作等边△ADE,连接CE. (1)、如图1,当点D在线段BC上时,求证:BD=CE;(2)、如图2,当点D在线段BC的反向延长线上时,若∠BAE=α,求∠DEC的度数;(用含α的代数式表示)(3)、如图3,当点D在线段BC的延长线上时,若BD⊥DE,且S△ABC=4,求△ACF的面积.
(1)、如图1,当点D在线段BC上时,求证:BD=CE;(2)、如图2,当点D在线段BC的反向延长线上时,若∠BAE=α,求∠DEC的度数;(用含α的代数式表示)(3)、如图3,当点D在线段BC的延长线上时,若BD⊥DE,且S△ABC=4,求△ACF的面积.