陕西省安康市2023年中考数学第一次模拟考试卷

试卷更新日期：2023-03-15 类型：中考模拟

进入出卷网下载

一、单选题

1. $- \frac{1}{3}$ 的倒数是（）

A、3 B、-3 C、 $\frac{1}{3}$ D、1

查看试题解析
2. 如图，直线 $A B 、 C D$ 相交于点O， $O E ⊥ C D$ ，若 $∠ A O E = 50 °$ ，则 $∠ B O D$ 的度数为（）

A、 $30 °$ B、 $40 °$ C、 $45 °$ D、 $50 °$

查看试题解析
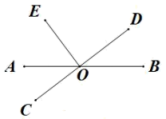3. 下列计算结果正确的是（）

A、 $x \cdot x^{2} = x^{3}$ B、 $3 x^{6} \div x^{2} = 3 x^{3}$ C、 $2 x^{2} \cdot 3 x^{3} = 6 x^{6}$ D、 ${(3 x^{3})}^{2} = 6 x^{6}$

查看试题解析
4. 如图，平行四边形ABCD中，对角线AC、BD相交于点O，则下列结论中不正确的是（　　）

A、当AB＝BC时，它是菱形 B、当AC⊥BD时，它是菱形 C、当AC＝BD时，它是矩形 D、当AC垂直平分BD时，它是正方形

查看试题解析
5. 如图，在 $R t △ A B C$ 中， $C D$ 为斜边 $A B$ 上的中线，过点D作 $D E ⊥ A B$ ，连接 $A E 、 B E$ ，若 $C D = 4$ ， $A E = 5$ ，则 $D E$ 的长为（）

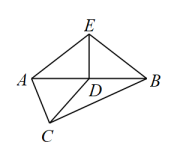A、2 B、3 C、4 D、5

查看试题解析
6. 在平面直角坐标系中，直线 $l_{1}$ ：y＝x+3与直线 $l_{2}$ ：y＝mx+n交于点A（-1，2），则关于x、y的方程组 ${\begin{array}{l} y = x + 3 \\ y = m x + n \end{array}$ 的解为（）

A、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = - 1 \end{array}$ C、 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ D、 ${\begin{array}{l} x = - 1 \\ y = - 2 \end{array}$

查看试题解析
7. 如图，已知在 $⊙ O$ 中， $∠ D O A ： ∠ A O B = 2 ： 1$ ，且 $∠ A C B = 25 °$ ，则 $∠ D$ 的度数为（）

A、 $40 °$ B、 $45 °$ C、 $50 °$ D、 $55 °$

查看试题解析
8. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，其顶点为 $(\frac{1}{2} ， 1)$ ，有下列结论：① $a c < 0$ ；②函数最大值为1；③ $b^{2} - 4 a c < 0$ ；④ $2 a + b = 0$ ，其中，正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

9. 计算 $2^{5} \div 0 . 5^{- 4} - {(2 π - 6.28)}^{0}$ 的结果是.

查看试题解析
10. 已知a、b、c在数轴上的位置如图所示，化简： $| 2 a | - | a + c | + | b - 1 | =$

查看试题解析
11. 五角星是我们生活中常见的一种图形，如图，C，D为线段AB的黄金分割点，AB=2，则五边形CDEFG的周长为.

查看试题解析
12. 如图，过反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象上一点A作 $A B ⊥ x$ 轴于点B，连接 $A O$ ，若 $S_{△ A O B} = 3$ ，则k的值为.

查看试题解析
13. 如图，在菱形ABCD中，AB＝6， $∠ A B C = 60 °$ ， AC与BD交于点O，点N在AC上且AN＝2，点M在BC上且BM＝ $\frac{2}{3}$ BC，P为对角线BD上一点，则PM-PN的最大值为.

查看试题解析

三、解答题

14. 计算：

(1)、 $\sqrt[3]{64} - \sqrt{81} + \sqrt[3]{125} + \sqrt{(- 3)^{2}} - \sqrt{4} - (\sqrt[3]{- 2})^{3}$

(2)、 $- 1^{2} + | \sqrt{5} - 3 | - \sqrt{16} + \sqrt[3]{8} + (- 2)^{2} - (- \sqrt{5})$

查看试题解析
15. 解不等式组： ${\begin{array}{l} x + 2 > - 1 \\ x - 5 ⩽ 3 (x - 1) \end{array}$

查看试题解析
16. 化简： $(1 - \frac{2}{x - 1}) \cdot \frac{x^{2} - x}{x^{2} - 6 x + 9}$

查看试题解析
17. 如图，在 $△ A B C$ 中， $∠ A B C = 60 °$ ，将 $△ A B C$ 绕点B逆时针旋转 $60 °$ 到 $△ D B E ， D E$ 的延长线与 $A C$ 相交于点F，连接 $D A 、 B F$ ，求证： $D A ∥ B C$ .

查看试题解析
18. 如图，在等腰直角 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ， $B N ⊥ C N$ 于 $N$ ， $A M ⊥ C N$ 于 $M$ ，且 $B N = 4$ ， $A M = 7$ ，求 $M N$ 的长.

查看试题解析
19. 如图，在平面直角坐标系中， $△ A B C$ 的顶点坐标分别为 $A (1 ， 2) ， B (3 ， 1) ， C (- 2 ， - 1)$ .在图中作出 $△ A B C$ 关于y轴对称的 $△ A_{1} B_{1} C_{1}$ ，并写出点B、C的对应点 $B_{1}$ 、 $C_{1}$ 的坐标.

查看试题解析
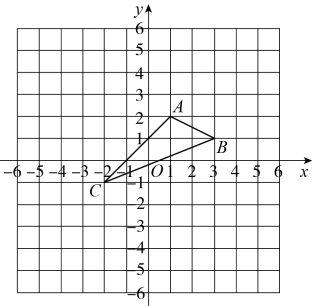20. 实现民族伟大复兴是近代中华民族最伟大的梦想，需要每位少年团结奋斗，同心共圆中国梦！在一个不透明的口袋里装有五个小球，分别标注汉字“共”、“圆”、“中”、“国”、“梦”，除汉字不同之外，小球没有任何区别，从中随机取出一个小球.

(1)、取出的小球上恰好标有“国”字的概率是多少？

(2)、取出的小球不放回，再从中任取一球.请用树状图或列表法，求取出的两个球上的汉字恰能组成“中国”或“圆梦”的概率.

查看试题解析
21. 某数学兴趣小组决定利用所学知识测量一古建筑的高度.如图2，古建筑的高度为 $A B$ ，在地面 $B C$ 上取E，G两点，分别竖立两根高为 $1.5 m$ 的标杆 $E F$ 和 $G H$ ，两标杆间隔 $E G$ 为 $26 m$ ，并且古建筑 $A B$ ，标杆 $E F$ 和 $G H$ 在同一竖直平面内.从标杆 $E F$ 后退 $2 m$ 到D处（即 $E D = 2 m$ ），从D处观察A点，A、F、D三点成一线；从标杆 $G H$ 后退 $4 m$ 到C处（即 $C G = 4 m$ ），从C处观察A点，A、H、C三点也成一线.已知B、E、D、G、C在同一直线上， $A B ⊥ B C$ ， $E F ⊥ B C$ ， $G H ⊥ B C$ ，请你根据以上测量数据，帮助兴趣小组求出该古建筑 $A B$ 的高度.

查看试题解析
22. 甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地，轿车比货车晚出发1.5小时，两车距离甲地的距离y（千米）与时间x（小时）之间的函数关系如图所示，请根据图象解答下列问题：

(1)、货车的速度为； $B C$ 段的函数表达式为.

(2)、轿车出发后，用了多长时间追上货车？

(3)、当货车行驶多长时间，两车相距15千米？

查看试题解析
23. 某校为了了解本校学生“上周内做家务劳动所用的时间”（简称“劳动时间”）情况，在本校随机调查了100名学生的“劳动时间”，并进行统计，绘制了如下统计表：
组别
“劳动时间”t/分钟
频数
组内学生的平均“劳动时间”/分钟
A
$t < 60$
8
50
B
$60 \leq t < 90$
16
75
C
$90 \leq t < 120$
40
105
D
$t \geq 120$
36
150
根据上述信息，解答下列问题：

(1)、这100名学生的“劳动时间”的中位数落在组；

(2)、求这100名学生的平均“劳动时间”；

(3)、若该校有1200名学生，请估计在该校学生中，“劳动时间”不少于90分钟的人数.

查看试题解析
24. 在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 90 °$ ， $A D$ 是 $△ A B C$ 的角平分线.

(1)、如图1，点E、F分别是线段 $C D$ 、 $A D$ 上的点，且 $D E = D F$ ， $A E$ 与 $B F$ 的延长线交于点G，则 $A E$ 与 $B F$ 的数量关系是，位置关系是；

(2)、如图2，点E、F分别在 $D C$ 和 $D A$ 的延长线上，且 $D E = D F$ ， $E A$ 的延长线交 $B F$ 于点G.
①（1）中的结论还成立吗？如果成立，请给出证明；如果不成立，请说明理由；
②连接 $D G$ ，若 $D G = 4 \sqrt{2}$ ， $D E = 6$ ，求 $E G$ 的长.

查看试题解析
25. 对于向上抛的物体，如果空气阻力忽略不计，有下面的关系式： $h = v_{0} t - \frac{1}{2} g t^{2}$ （ $h$ 是物体离起点的高度， $v_{0}$ 是初速度， $g$ 是重力系数，取 $10 m / s^{2}$ ， $t$ 是抛出后经过的时间）．杂技演员抛球表演时，以 $10 m / s$ 的初速度把球向上拋出．

(1)、球抛出后经多少秒回到起点？

(2)、几秒后球离起点的高度达到 $1.8 m$ ？

(3)、球离起点的高度能达到 $6 m$ 吗？请说明理由．

查看试题解析
26. 如果一个三角形的一个内角等于另一个内角的2倍，我们称这样的三角形为倍角三角形，并称这两个角的公共边为底边.

例如：若△ABC中，∠A＝2∠B，则△ABC为以边AB为底边的倍角三角形.

(1)、已知△ABC为倍角三角形，且 $∠ A B C ＝ 2 ∠ C$ .
①如图1，若BD为△ABC的角平分线，则图中相等的线段有，图中相似三角形有；
②如图2，若AC的中垂线交边BC于点E，连接AE，则图中等腰三角形有.

(2)、【问题解决】
如图3，现有一块梯形板材ABCD， $A D ∥ B C$ ， ∠A＝90°，AB＝48，BC＝132，AD＝68.工人师傅想用这块板材裁出一个△BCP型部件，使得点P在梯形ABCD的边上，且△BCP为以BC为底边的倍角三角形.工人师傅在这块板材上的作法如下：
①作BC的中垂线l交BC于点E；

②在BC上方的直线l上截取EF＝33，连接CF并延长，交AD于点P；

③连接BP，得△BCP.

1）请问，若按上述作法，裁得的△BCP型部件是否符合要求？请证明你的想法.

2）是否存在其它满足要求的△BCP？若存在，请画出图形并求出CP的长；若不存在，请说明理由.

查看试题解析

组别	“劳动时间”t/分钟	频数	组内学生的平均“劳动时间”/分钟
A	$t < 60$	8	50
B	$60 \leq t < 90$	16	75
C	$90 \leq t < 120$	40	105
D	$t \geq 120$	36	150