海南省定安县2023年中考数学第一次模拟试题
试卷更新日期:2023-03-15 类型:中考模拟
一、单选题
-
1. 下列各数中,3的相反数的倒数是( )A、3 B、-3 C、 D、2. 一种花粉颗粒直径约为0.0000078米,数字0.0000078用科学记数法表示为( )A、 B、 C、 D、3. 用3个大小相同的小正方体搭成的几何体,从三个方向看到的形状图如图所示,则这个几何体可能是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 将不等式的解集表示在数轴上,正确的是( )A、
4. 将不等式的解集表示在数轴上,正确的是( )A、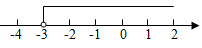 B、
B、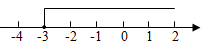 C、
C、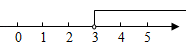 D、
D、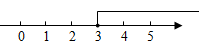 5. 对于一组数据﹣1、4、﹣1、2下列结论不正确的是( )A、平均数是1 B、众数是-1 C、中位数是0.5 D、方差是3.56. 下列分式方程中,解为的是( )A、 B、 C、 D、7. 若反比例函数的图象经过点 , 则该函数图象一定经过( )A、 B、 C、 D、8. 如图,在中,点D和E分别是边和的中点,连接 , 与交于点O,若的面积为1,则的面积为( )
5. 对于一组数据﹣1、4、﹣1、2下列结论不正确的是( )A、平均数是1 B、众数是-1 C、中位数是0.5 D、方差是3.56. 下列分式方程中,解为的是( )A、 B、 C、 D、7. 若反比例函数的图象经过点 , 则该函数图象一定经过( )A、 B、 C、 D、8. 如图,在中,点D和E分别是边和的中点,连接 , 与交于点O,若的面积为1,则的面积为( )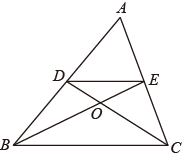 A、6 B、9 C、12 D、13.5
A、6 B、9 C、12 D、13.5二、填空题
-
9. , , 则.10. 正十边形的每一个内角的度数为.11. 下列图案均是由边长相同的小正方形按一定的规律构成:第1个图中有1个小正方形,第2个图中有3个小正方形,……,依此规律,则第5个图中有个小正方形,第n个图中有个小正方形(用含n的代数式表示).

三、解答题
-
12. 计算:(1)、;(2)、.13. 阅读理解:
为打造陶子河沿岸的风景带,有一段长为360米的河道整治任务由A、B两个工程队先后接力完成,A工程队每天整治24米,B工程队每天整治16米,共用20天.
(1)、根据题意,甲乙两个同学分别列出了尚不完整的方程组如下:甲: 乙:
根据甲、乙两名同学所列的方程组,请你分别指出未知数 , 表示的意义,并且补全甲、乙两名同学所列的方程组:
甲:表示 ▲ , 表示 ▲ ;
乙:表示 ▲ , 表示 ▲ ;
(2)、求出其中一个方程组的解,并回答A、B两工程队分别整治河道多少米?14. 为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):选择意向
文学鉴赏
国际象棋
音乐舞蹈
书法
其他
所占百分比
20%
10%
5%
根据统计图表的信息,解答下列问题:
 (1)、本次抽样调查的学生有人;(2)、统计表中的 , ;(3)、选择“国际象棋”的学生有人;(4)、若该校共有名学生,试估计全校选择“音乐舞蹈”社团的学生有人.15. 如图,是的直径,为⨀O上一点,平分交⨀O于点 , 过点作交的延长线于点.
(1)、本次抽样调查的学生有人;(2)、统计表中的 , ;(3)、选择“国际象棋”的学生有人;(4)、若该校共有名学生,试估计全校选择“音乐舞蹈”社团的学生有人.15. 如图,是的直径,为⨀O上一点,平分交⨀O于点 , 过点作交的延长线于点.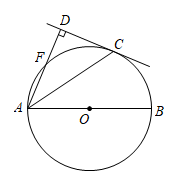 (1)、求证:是的切线.(2)、若 , , 求半径.
(1)、求证:是的切线.(2)、若 , , 求半径.

