海南省昌江黎族自治县2023年中考数学第一次模拟试题
试卷更新日期:2023-03-15 类型:中考模拟
一、单选题
-
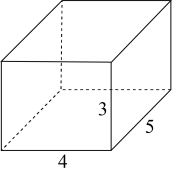
1. 有理数的相反数为( )A、 B、5 C、 D、-52. 芝麻作为食品和药物,均被广泛使用,经测算一粒芝麻的质量约为0.00000201kg,用科学记数法表示一粒芝麻的质量应为( )A、 B、 C、 D、3. 如图长方体的左视图是( )
 A、
A、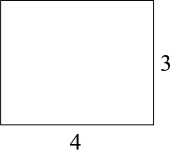 B、
B、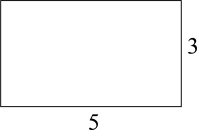 C、
C、 D、
D、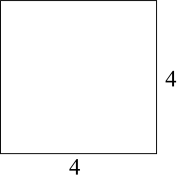 4. 若 , 则x的取值范围是( )A、 B、 C、 D、5. 下列命题中,属于真命题的是( )A、如果 , 那么与是对顶角 B、三角形的一个外角大于任何一个内角 C、两直线平行,同旁内角相等 D、等角的余角相等6. 在某县中小学安全知识竞赛中,参加决赛的6个同学获得的分数分别为(单位:分):95、97、97、96、98、99,对于这6个同学的成绩下列说法正确的是( )A、众数为95 B、极差为3 C、平均数为96 D、中位数为977. 分式方程的解是( )A、 B、 C、 D、无解8. 如图,、、三点在正方形网格的格点上,若将绕点A逆时针旋转得到 , 则的值为( )
4. 若 , 则x的取值范围是( )A、 B、 C、 D、5. 下列命题中,属于真命题的是( )A、如果 , 那么与是对顶角 B、三角形的一个外角大于任何一个内角 C、两直线平行,同旁内角相等 D、等角的余角相等6. 在某县中小学安全知识竞赛中,参加决赛的6个同学获得的分数分别为(单位:分):95、97、97、96、98、99,对于这6个同学的成绩下列说法正确的是( )A、众数为95 B、极差为3 C、平均数为96 D、中位数为977. 分式方程的解是( )A、 B、 C、 D、无解8. 如图,、、三点在正方形网格的格点上,若将绕点A逆时针旋转得到 , 则的值为( ) A、 B、 C、 D、9. 若反比例函数的图象经过点 , 则该函数图象一定经过( )A、 B、 C、 D、10. 如图,已知 , 若 , 则的度数为( )
A、 B、 C、 D、9. 若反比例函数的图象经过点 , 则该函数图象一定经过( )A、 B、 C、 D、10. 如图,已知 , 若 , 则的度数为( ) A、80° B、90 C、100° D、11011. 如图,直角梯形中, , 将腰绕点D逆时针方向旋转并缩短,恰好使 , 连接 , 则的面积是( )
A、80° B、90 C、100° D、11011. 如图,直角梯形中, , 将腰绕点D逆时针方向旋转并缩短,恰好使 , 连接 , 则的面积是( )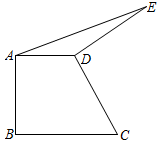 A、1 B、2 C、3 D、412. 如图,在中,点分别是的中点,若四边形的面积是 , 则的面积是( )
A、1 B、2 C、3 D、412. 如图,在中,点分别是的中点,若四边形的面积是 , 则的面积是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 分解因式:.14. 正n边形的一个内角度数是一个外角度数的3倍,则n=.15. 如图,点为内一点,分别作出点关于 , 的对称点 , , 连结交于 , 交于 , 若线段的长为 , 则的周长为.
 16. 用棋子摆出下列一组图形,按图上所显示的规律继续摆下去,摆到第100个图形时,这组图形总共用了枚棋子.
16. 用棋子摆出下列一组图形,按图上所显示的规律继续摆下去,摆到第100个图形时,这组图形总共用了枚棋子.
三、解答题
-
17. 计算:(1)、;(2)、.18. 西溪中学计划对新教学楼外墙进行粉刷装饰.若甲、乙两个装饰公司合作施工, 则共需要6天完成,学校总共需要支付9.6万元;若甲装饰公司先单独施工2天,则乙装饰公司 单独完成剩下的装饰工作还需要8天,学校总共需要支付9.2万元.(1)、求甲、乙两个装饰公司平均每天分别收取的费用.(2)、若设甲装饰公司每天完成的工作量为a,乙装饰公司每天完成的工作量为b,现在仅指定
一家装饰公司独立完成施工,选择哪家公司的总费用最低,并求出最低费用.
19. 为了解学生参加户外活动的情况,某中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题: (1)、被抽样调查的学生有 ▲ 人,并补全条形统计图.(2)、每天户外活动2小时对应的圆心角度数是.(3)、该校共有2000名学生,请估计该校每天户外活动时间超过1小时的学生有多少人?20. 为测量某机场东西两栋建筑物、之间的距离.如图,勘测无人机在点处,测得建筑物的俯角为 , 的距离为千米,然后沿着平行于的方向飞行千米到点处,测得建筑物的俯角为.参考数据: , , , , , .
(1)、被抽样调查的学生有 ▲ 人,并补全条形统计图.(2)、每天户外活动2小时对应的圆心角度数是.(3)、该校共有2000名学生,请估计该校每天户外活动时间超过1小时的学生有多少人?20. 为测量某机场东西两栋建筑物、之间的距离.如图,勘测无人机在点处,测得建筑物的俯角为 , 的距离为千米,然后沿着平行于的方向飞行千米到点处,测得建筑物的俯角为.参考数据: , , , , , . (1)、无人机距离地面的飞行高度是多少千米?(2)、求该机场东西两栋建筑物、之间的距离.结果精确到0.01千米21. 将一块足够大的直角三角板的直角顶点P放在边长为1的正方形ABCD的对角线AC上滑动,一条直角边始终经过点B,另一条直角边与射线DC交于点E.
(1)、无人机距离地面的飞行高度是多少千米?(2)、求该机场东西两栋建筑物、之间的距离.结果精确到0.01千米21. 将一块足够大的直角三角板的直角顶点P放在边长为1的正方形ABCD的对角线AC上滑动,一条直角边始终经过点B,另一条直角边与射线DC交于点E.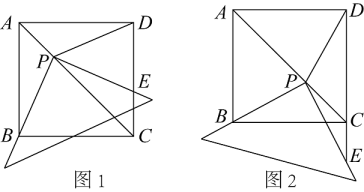 (1)、当点E在边DC上时(如图1),求证:
(1)、当点E在边DC上时(如图1),求证:①△PBC ≌△PDC;
②PB=PE.
(2)、当点E在边DC的延长线上时(如图2),(1)中的结论②还成立吗?如果不成立,请说明理由;如果成立,请给予证明.22. 如图,在平面直角坐标系中,抛物线 的图象与坐标轴相交于 、 、 三点,其中 点坐标为 , 点坐标为 ,连接 、 .动点 从点 出发,在线段 上以每秒 个单位长度向点 做匀速运动;同时,动点 从点 出发,在线段 上以每秒1个单位长度向点 做匀速运动,当其中一点到达终点时,另一点随之停止运动,连接 ,设运动时间为 秒. (1)、求 、 的值;(2)、在 、 运动的过程中,当 为何值时,四边形 的面积最小,最小值为多少?(3)、在线段 上方的抛物线上是否存在点 ,使 是以点 为直角顶点的等腰直角三角形?若存在,请求出点 的坐标;若不存在,请说明理由.
(1)、求 、 的值;(2)、在 、 运动的过程中,当 为何值时,四边形 的面积最小,最小值为多少?(3)、在线段 上方的抛物线上是否存在点 ,使 是以点 为直角顶点的等腰直角三角形?若存在,请求出点 的坐标;若不存在,请说明理由.