贵州省遵义市播州区2023年九年级上学期第一次模拟考试数学试题

试卷更新日期：2023-03-15 类型：中考模拟

进入出卷网下载

一、单选题

1. “国际禁毒日”是每年的（）

A、7月9日 B、6月26日 C、12月1日 D、5月17日

查看试题解析
2. 下列数学符号中，既是中心对称图形又是轴对称图形的是（）

A、 $π$ B、 $β$ C、 $λ$ D、 $θ$

查看试题解析
3. 遵义市2022年上半年GDP约为218100000000元，与2021年上半年相比增长了10.61％，将数据218100000000 用科学记数法表示为（）

A、 $2181 \times 1 0^{4}$ B、 $2.181 \times 1 0^{11}$ C、 $2.181 \times 1 0^{10}$ D、 $21.81 \times 1 0^{10}$

查看试题解析
4. 如图，直线 $a$ ， $b$ 被直线 $c$ 所截，且 $a ∥ b$ .若 $∠ 1 = 60 °$ ，则 $∠ 2$ 的度数为（）

A、60° B、50° C、40° D、30°

查看试题解析
5. 下列计算正确的是（）

A、 ${(m - n)}^{2} = m^{2} - n^{2}$ B、 $m^{5} + m^{5} = 2 m^{10}$ C、 $m^{6} \div m^{3} = m^{2}$ D、 $a^{2} b^{2} = {(a b)}^{2}$

查看试题解析
6. 如图，四边形 $A B C D$ 是平行四边形，其对角线 $A C$ ， $B D$ 相交于点 $O$ ，下列理论一定成立的是（）

A、 $A C = B D$ B、 $A C ⊥ B D$ C、 $A B = C D$ D、 $A B = A D$

查看试题解析
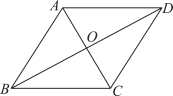7. 将4个全等的小长方形按如图所示的方式摆放拼成一个大长方形 $A B C D$ ，且 $A B = 12 c m$ .设小长方形的宽为 $x c m$ ，长为 $y c m$ ，依题意列二元一次方程组正确的是（）

A、 ${\begin{array}{l} x + y = 12 \\ y = 3 x \end{array}$ B、 ${\begin{array}{l} x - y = 12 \\ y = 3 x \end{array}$ C、 ${\begin{array}{l} x + y = 12 \\ x = 3 y \end{array}$ D、 ${\begin{array}{l} 3 x = 12 \\ y = x \end{array}$

查看试题解析
8. 已知 $x_{1}$ ， $x_{2}$ 是关于 $x$ 的方程 $x^{2} - x - 2023 = 0$ 的两个根，则 $x_{1}^{2} - 2 x_{1} - x_{2}$ 的值为（）

A、2023 B、2022 C、2021 D、2020

查看试题解析
9. 二次函数 $y = a x^{2} - 2 x + c$ 和一次函数 $y = a x + c$ （ $a$ ， $c$ 都是常数，且 $a \neq 0$ ）在同一平面直角坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 某农场种植基地2021年蔬菜产量为100吨，预计2023年蔬菜产量将达到121吨.若蔬菜产量的年平均增长率相同，则年平均增长率为（）

A、-210% B、-10% C、5% D、10%

查看试题解析
11. 如图所示的是 $3 \times 2$ 的正方形网格，每个小正方形的顶点称为格点.线段 $A B$ ， $C D$ 的端点均在格点上，线段 $A B$ ， $C D$ 交于点 $O$ ，则 $∠ B O D$ 的度数为（）

A、 $30 °$ B、 $45 °$ C、 $50 °$ D、 $60 °$

查看试题解析
12. 如图，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象与一次函数 $y = - x + c$ 的图象交于 $A$ ， $B$ 两点，二次函数的对称轴为 $x = 1$ ， $m$ ， $n (m > n)$ 是关于 $x$ 的方程 $a x^{2} + b x + c = 0$ 的两个根，有以下结论：① $c < 0$ ；② $m + n = 2$ ；③ $a + b = \frac{1}{m}$ ；④当 $0 < x < m$ 时， $a x^{2} + (b + 1) x > 0$ .其中正确的结论是（）

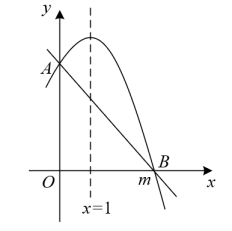A、①②③④ B、①③④ C、②③④ D、②④

查看试题解析

二、填空题

13. 计算： $\sqrt{18} - \sqrt{8} =$ .

查看试题解析
14. 定义新运算： $∩$ ，如 ${a ， b ， c} ∩ {c ， b ， m} = {b ， c}$ ，则 ${2 ， 8 ， 15 ， 20} ∩ {3 ， 2 ， 15} =$ {}.

查看试题解析
15. 若一个函数的图象关于 $y$ 轴对称，则称这个函数为偶函数，如二次函数 $y = - x^{2}$ 是偶函数.若二次函数 $y = 2 x^{2} + (3 - a) x + 8$ 是偶函数，则 $a$ 的值为.

查看试题解析
16. 如图， $D$ 为等边三角形 $A B C$ 内一点， $A D = 10$ ， $B D = 6$ ， $C D = 8$ ，将 $△ B C D$ 绕点 $C$ 顺时针旋转 $60 °$ 得到 $△ A C E$ ，则图中阴影部分的面积为.

查看试题解析

三、解答题

17.

(1)、计算： $| - \sqrt{2} | + {(\frac{1}{2})}^{- 2} - \sqrt{8} \times \frac{1}{2}$ ；

(2)、先化简： $(\frac{x^{2} + 2 x + 1}{x^{2} - 1} + \frac{x + 1}{x - 1}) \div \frac{x + 1}{x^{2} - x}$ ，再从不等式组 ${\begin{array}{l} 2 - x < 4 ， ① \\ 2 (x - 3) \leq - 2 ② \end{array}$ 的解集中选一个合适的整数 $x$ 的值代入求值.

查看试题解析
18. 如图1，计划在长为30米、宽为20米的矩形地面上修筑两条同样宽的道路①、②（图中阴影部分），设道路①、②的宽为 $x$ 米，剩余部分为绿化.

(1)、道路①的面积为平方米；道路②的面积为平方米（都用含 $x$ 的代数式表示）.

(2)、如图2，根据实际情况，将计划修筑的道路①、②改为同样宽的道路③（图中阴影部分），若道路的宽依然为 $x$ 米，剩余部分为绿化，且绿化面积为551平方米，求道路的宽度.

查看试题解析

19. 某校组织八，九年级各100名学生举行“喜迎二十大，奋进新征程”征文竞赛，现分别在八，九年级中各随机抽取10名学生的竞赛成绩（单位：分）进行统计、整理如下：

收集数据：

八年级：74，76，79，81，84，86，87，90，90，93.

九年级：76，81，81，83，84，84，84，85，90，92.

整理数据：

八，九年级竞赛成绩各分数段整理如下：

	$70 \leq x < 80$	$80 \leq x < 90$	$90 \leq x < 100$
八年级	$a$	4	3
九年级	1	7	2

分析数据：

八，九年级成绩的平均数、中位数、众数和方差整理如下：

	平均数	中位数	众数	方差
八年级	84	$b$	90	36.4
九年级	84	84	$c$	18.4

问题解决：

根据以上信息，解答下列问题：

(1)、直接写出

a =

，

b =

，

c =

(2)、根据上述数据分析，该校八，九年级中哪个年级的竞赛成绩更优异？请说明理由（写出一条理由即可）.

(3)、规定竞赛成绩不低于85分记为“优秀”，请分别估计这两个年级竞赛成绩达到“优秀”的学生人数.

查看试题解析

20. 小明学习菱形时，对矩形 $A B C D$ 进行了画图探究 $(A D > A B)$ ，其作法和图形如下：
①连接 $B D$ ；
②分别以点 $B$ ， $D$ 为圆心，大于 $B D$ 长的一半为半径作弧，两弧相交于 $M$ ， $N$ 两点，作直线 $M N$ 交 $B D$ 于点 $O$ ，交 $A D$ 于点 $E$ ，交 $B C$ 于点 $F$ ；
③连接 $B E$ ， $D F$ .

(1)、根据以上作法，判断四边形 $B F D E$ 的形状，并说明理由；

(2)、若 $A B = 4$ ， $A D = 8$ ，求四边形 $B F D E$ 的面积.

查看试题解析
21. 某商场购进一批衣服，每件的进价为80元，出于营销考虑，要求每件衣服的售价不低于80元且不高于150元，在销售过程中发现该衣服每周的销售量 $y$ （件）与每件衣服的售价 $x$ （元）之间满足的函数关系如图所示.

(1)、求 $y$ 关于 $x$ 的函数关系式及 $x$ 的取值范围；

(2)、若商场每周销售该衣服获得的利润为1100元，则每件衣服的售价是多少元？

(3)、设该商场每周销售这种衣服所获得的利润为 $w$ 元，则将该衣服的销售单价定为多少元时，才能使所获利润最大？最大利润是多少？

查看试题解析
22. 如图，二次函数 $y = a x^{2} + b x + c$ 的图象与 $x$ 轴交于 $A (- 1 ， 0)$ ， $B (3 ， 0)$ 两点，与 $y$ 轴交于点 $C (0 ， 3)$ .

(1)、求二次函数的解析式和图象的对称轴；

(2)、若该二次函数在 $m - 1 \leq x \leq m$ 内有最大值 $2 m$ ，求 $m$ 的值.

查看试题解析
23. 如图1，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 2 α$ ，点 $D$ ， $E$ 均在边 $B C$ 上（点 $D$ 在点 $E$ 的左侧），且 $∠ D A E = α$ .

(1)、如图1，将 $△ A B D$ 绕点 $A$ 逆时针旋转 $2 α$ 得到 $△ A C F$ ，连接 $E F$ ，求证： $△ A D E ≌ △ A F E$ ；

(2)、如图2，若 $∠ B A C = 90 °$ ，求证： $D E^{2} = B D^{2} + E C^{2}$ ；

(3)、如图3，若 $∠ B A C = 60 °$ ， $A B = A C = 5$ ， $B D = 1$ ，求线段 $C E$ 的长度.

查看试题解析