浙江省绍兴市诸暨市暨阳教育共同体2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-03-15 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $a^{4} + a^{3} = a^{7}$ B、 $(a^{3})^{2} = a^{5}$ C、 $a^{6} \div a^{3} = a^{3}$ D、 $(a - b)^{2} = a^{2} - b^{2}$

查看试题解析
2. 已知某种植物花粉的直径为0.000035，那么用科学记数法可表示为（）

A、 $3.5 \times 1 0^{4}$ 米 B、 $3.5 \times 1 0^{- 4}$ 米 C、 $3.5 \times 1 0^{5}$ 米 D、 $3.5 \times 1 0^{- 5}$ 米

查看试题解析
3. 如图，直线 $A B$ ， $C D$ 被直线 $E F$ 所截，则 $∠ 1$ 与 $∠ 2$ 是（）

A、同位角 B、内错角 C、同旁内角 D、对顶角

查看试题解析
4. 下列各式不能使用平方差公式的是（）

A、 $(2 a + 3 b) (2 a - 3 b)$ B、 $(2 a - 3 b) (- 2 a - 3 b)$ C、 $(- 2 a + 3 b) (- 2 a - 3 b)$ D、 $(- 2 a + 3 b) (3 b - 2 a)$

查看试题解析
5. 如图，一根直尺EF压在三角板 $3 0^{0}$ 的角∠BAC上，欲使CB∥EF，则应使∠ENB的度数为（）

A、 $10 0^{0}$ B、 $11 0^{0}$ C、 $12 0^{0}$ D、 $13 0^{0}$

查看试题解析
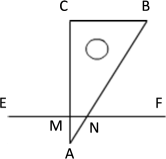6. (3a+2)(4a²－a－1)的结果中二次项系数是（）

A、－3 B、8 C、5 D、－5

查看试题解析
7. 若 $x^{2} - 2 (k - 1) x + 4$ 是完全平方式，则k的值为（）

A、 $\pm 1$ B、 $\pm 3$ C、 $- 1$ 或3 D、1或 $- 32$

查看试题解析
8. 多项式 $77 x^{2} - 13 x - 30$ 可因式分解成 $(7 x + a) (b x + c)$ ，其中 $a$ ， $b$ ， $c$ 均为整数， $b + a c$ 的值为（）

A、 $0$ B、 $10$ C、 $22$ D、 $- 19$

查看试题解析
9. 有3张边长为a的正方形纸片，8张边长分别为a、b（b＞a）的矩形纸片，10张边长为b的正方形纸片，从其中取出若干张纸片，每种纸片至少取一张，把取出的这些纸片拼成个正方形（按原纸张进行无空隙、无重叠拼接），则拼成的正方形的边长最长可以为（）

A、a+5b B、a+4b C、2a+2b D、a+3b

查看试题解析
10. 将一副三角板顶点重合，三角板ABC绕点A顺时针转动的过程中，∠EAB度数符合下列条件时，三角尺不存在一组边平行的是（三角板边AB＝AE）（）

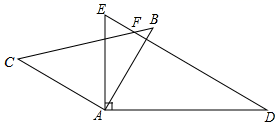A、∠EAB＝30° B、∠EAB＝45° C、∠EAB＝60° D、∠EAB＝75°

查看试题解析

二、填空题

11. $(- 2 a^{3})^{2}$ 的计算结果是.

查看试题解析
12. 因式分解： $x^{2} - 4 =$ .

查看试题解析
13. 计算： $(- 0.125)^{2022} \times 8^{2022} =$ .

查看试题解析
14. 已知 ${\begin{array}{l} x = t - 4 \\ y = 7 - t \end{array}$ ，那么用 $x$ 表示 $y$ 的式子为.

查看试题解析
15. 把 $3 \times 27 \times 81 \times 3^{n}$ 写成 $a^{n}$ 的形式是.

查看试题解析
16. 如图将边长为 $5 c m$ 的等边 $△ A B C$ 沿边 $B C$ 向右平移 $2 c m$ 得到 $△ A' B' C'$ ，则四边形 $A A' C' C$ 的周长为.

查看试题解析
17. $b^{m} = 2$ ， $b^{n} = 3$ ，则 $b^{3 m - 2 n} =$ .

查看试题解析
18. 若（1-x）¹^-^3x=1，则x的取值有个.

查看试题解析
19. 为了求 $1 + 2 + 2^{2} + \dots + 2^{2021}$ 的值，可令 $S = 1 + 2 + 2^{2} + \dots + 2^{2021}$ ，则 $2 S = 2 + 2^{2} + \dots + 2^{2022}$ ，因此 $2 S - S = 2^{2022} - 1$ ，所以 $1 + 2 + 2^{2} + \dots + 2^{2021} = 2^{2022} - 1 ．$ 按照以上推理计算出 $1 + 3^{- 1} + 3^{- 2} + \dots + 3^{- 2021}$ 的值是.

查看试题解析
20. 如图所示，已知射线CB//OA， $∠ C = ∠ O A B = 120 °$ ， $E$ 、 $F$ 在 $C B$ 上，且满足 $∠ F O B = ∠ A O B$ ， $O E$ 平分 $∠ C O F$ .

(1)、则 $∠ E O B$ 的度数为；

(2)、在平行移动 $A B$ 的过程中，当 $∠ O E C = ∠ O B A$ 时， $∠ O E C =$ 度.

查看试题解析

三、解答题

21.

(1)、计算： $3^{- 2} + (π - 3)^{0} + (- 1)^{2021}$ ；

(2)、化简： $(m - n)^{2} - m (m - 3 n)$ .

查看试题解析
22. 因式分解：

(1)、 $2 m^{3} - 8 m^{2} + 8 m$ ；

(2)、 $3 a x y^{3} - 12 a x^{3} y ．$

查看试题解析
23. 如图，已知AB//CD，点 $P$ 在直线 $A B$ 与直线 $C D$ 之间， $∠ C = 70 °$ ， $∠ E B P = 110 °$ .

(1)、试判断 $A C$ 与 $B P$ 之间的位置关系，并说明理由；

(2)、若 $P N$ 平分 $∠ B P M$ ， $∠ P N B = 30 °$ ，求 $∠ P M D$ 的度数.

查看试题解析
24. 某中学组织初一学生春游，原计划租用 $45$ 座汽车若干辆，但有 $15$ 人没有座位；若租用同样数量的 $60$ 座汽车，则多出一辆，且其余客车恰好坐满.已知 $45$ 座客车每日租金每辆 $220$ 元， $60$ 座客车每日租金为每辆 $300$ 元.

(1)、初一年级人数是多少？原计划租用 $45$ 座汽车多少辆？

(2)、可以单独租一种车，也可以同时租两种车，要使每个学生都有座位，怎样租用更合算？ $($ 通过计算加以说明 $)$

查看试题解析
25. 先阅读材料，再回答问题：
分解因式： $(a - b)^{2} - 2 (a - b) + 1$
解：设 $a - b = M$ ，则原式 $= M^{2} - 2 M + 1 = (M - 1)^{2}$
再将 $a - b = M$ 还原，得到：原式 $= (a - b - 1)^{2}$
上述解题中用到的是“整体思想”，它是数学中常用的一种思想，请你用整体思想解决下列问题：

(1)、分解因式： $(x + y) (x + y - 4) + 4$

(2)、若 $a$ 为正整数，则 $(a - 1) (a - 2) (a - 3) (a - 4) + 1$ 为整数的平方，试说明理由.

查看试题解析