浙江省绍兴市柯桥区联盟校2021-2022学年七年级下学期期中考试数学试题

试卷更新日期：2023-03-15 类型：期中考试

进入出卷网下载

一、单选题

1. 如图所示的四个图形中，∠1和∠2是同位角的是（）

A、②③ B、①②③ C、①②④ D、①④

查看试题解析
2. 下列各式中是二元一次方程的是（）

A、2x+y=6z B、 $\frac{1}{x} + 2 y = 3$ C、3x+2y=9 D、x-3=4y ²

查看试题解析
3. 下列等式，其中正确的个数是（）
①（-2x²y³）³=-6x⁶y⁹；
②（-a²ⁿ）³=a⁶ⁿ；
③（3a⁶）³=9a¹⁸；
④（-a）⁵+（-a²）³+（-a⁴）=a⁷；
⑤（-0.5）¹⁰⁰×2¹⁰¹=（-0.5×2）¹⁰⁰×2

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 如果 $\frac{1}{2}$ a^3xb^y与﹣a^2yb^x+1是同类项，则（）

A、 ${\begin{cases} x = - 2 \\ y = 3 \end{cases}$ B、 ${\begin{cases} x = 2 \\ y = - 3 \end{cases}$ C、 ${\begin{cases} x = - 2 \\ y = - 3 \end{cases}$ D、 ${\begin{cases} x = 2 \\ y = 3 \end{cases}$

查看试题解析
5. 将矩形ABCD沿AE折叠，得到如图所示的图形，已知∠CED′＝55°，则∠BAD′的大小是（）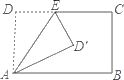

A、30° B、35° C、45° D、60°

查看试题解析
6. 下列计算正确的是（）

A、 $（ a + b) (a - 2 b) = a^{2} - a b - 2 b^{2}$ B、 $（ a - b) (- a + b) = a^{2} - b^{2}$ C、 $（ x - 2 y)^{2} = x^{2} - 2 x y - 4 y^{2}$ D、 $(4 x + 9 y) (4 x - 9 y) = 4 x^{2} - 9 y^{2}$

查看试题解析
7. 若x²＋2（k＋1）x＋4是完全平方式，则k的值为（）

A、＋1 B、-3 C、-1或3 D、1或-3

查看试题解析
8. 如图，将矩形ABCD沿GH折叠，点C落在点Q处，点D落在AB边上的点E处，若∠AGE＝36°，则∠GHC等于（）

A、110° B、108° C、106° D、112°

查看试题解析
9. 某校运动员分组训练，若每组7人，余3人；若每组8人，则缺5人；设运动员人数为x人，组数为y组，则列方程组为（）

A、 ${\begin{cases} 7 y = x + 3 \\ 8 y + 5 = x \end{cases}$ B、 ${\begin{cases} 7 y = x + 3 \\ 8 y - 5 = x \end{cases}$ C、 ${\begin{cases} 7 y = x + 3 \\ 8 y = x + 5 \end{cases}$ D、 ${\begin{cases} 7 y + 3 = x \\ 8 y - 5 = x \end{cases}$

查看试题解析
10. 如图，大长方形按如图方式分成5块，其中标号①，③，④的为正方形，标号②，⑤的为长方形，若要求出⑤与②的周长差，则只需知道下列哪个条件（）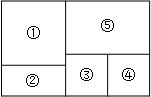

A、①的周长 B、②的周长 C、⑤的面积 D、③的面积

查看试题解析

二、填空题

11. 将方程5x﹣2y＝7变形成用y的代数式表示x，则x＝.

查看试题解析
12. 如图，将周长为14cm的△ABC沿射线BC方向平移3cm后得到△DEF，则四边形ABFD的周长为cm.

查看试题解析
13. 某种病毒变异后的直径约为0.000 000 056米，将这个数用科学记数法表示为米.

查看试题解析
14. 下列说法正确的有（填序号）：.
①同位角相等；

②在同一平面内，两条不相交的线段是平行线；

③在同一平面内，如果a//b，b//c，则a//c；

④在同一平面内，过直线外一点有且只有一条直线与已知直线平行.

查看试题解析
15. 如果方程组 ${\begin{array}{l} x + y = 3 \\ m x + n y = 8 \end{array}$ 与方程组 ${\begin{array}{l} x - y = 1 \\ m x - n y = 4 \end{array}$ 有相同的解，则 $m - n =$ .

查看试题解析
16. 已知 $3^{2 m} = 5$ ， $3^{2 n} = 10$ ，则 $9^{m - n}$ 的值是．

查看试题解析
17. 已知a＝9⁶ ， b＝3¹⁴ ， c＝27⁵ ，则a，b，c的大小关系用“＜”号连接为.

查看试题解析
18. 已知3x^2a＋b－³－5y^3a－2b＋2＝1是关于x，y的二元一次方程，则（a＋b）^b＝.

查看试题解析
19. 我们知道方程组 ${\begin{array}{l} 2 x + 3 y = 19 \\ 3 x + 4 y = 26 \end{array}$ 的解是 ${\begin{array}{l} x = 2 \\ y = 5 \end{array}$ ，现给出另一个方程组 ${\begin{array}{l} 2 (2 x + 4) + 3 (y + 3) = 19 \\ 3 (2 x + 4) + 4 (y + 3) = 26 \end{array}$ ，它的解是.

查看试题解析
20. 若一个正整数能表示为两个正整数的平方差，那么就称这个正整数为智慧数.如， $5^{2} - 3^{2} = 16$ ，则16是一个智慧数，5和3称为16的一对智慧分解数.则2019的智慧分解数有.

查看试题解析

三、解答题

21.

(1)、解方程组 ${\begin{array}{l} y = 2 x - 1 \\ x + 2 y = - 7 \end{array}$

(2)、因式分解：x³-4xy²

查看试题解析
22.

(1)、计算： $\sqrt{4} + (- 2013)^{0} - (\frac{1}{2})^{- 2}$

(2)、先化简，再求值： $（ 2 a + b)^{2} - (2 a - b) (2 a + b)$ ，其中 $a = - 1$ ， $b = \frac{1}{2}$ .

查看试题解析
23. 将下面的解答过程补充完整：
如图，点 $E$ 在 $D F$ 上，点 $B$ 在 $A C$ 上， $∠ 1 = ∠ 2$ ， $∠ C = ∠ D$ .试说明： $A C ∥ D F$ .
解：∵ $∠ 1 = ∠ 2$ （已知）
$∠ 1 = ∠ 3$ （             ）
∴ $∠ 2 = ∠ 3$ （             ）
∴  ▲   $∥$   ▲  （             ）
∴ $∠ C = ∠ A B D$ （             ）
∵ $∠ C = ∠ D$ （已知）
∴ $∠ D = ∠ A B D$ （             ）
∴ $A C ∥ D F$ （             ）

查看试题解析
24. 如图，已知∠A＝∠C，AD⊥BE，BC⊥BE，点E，D，C在同一条直线上.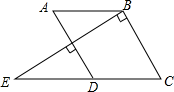

(1)、判断AB与CD的位置关系，并说明理由.

(2)、若∠ABC＝120°，求∠BEC的度数.

查看试题解析
25. 已知 $x + y = 3$ ，且 $(x + 3) (y + 3) = 20$ .

(1)、求 $x y$ 的值；

(2)、求 $x^{2} + 5 x y + y^{2}$ 的值；

(3)、求x－y的值

查看试题解析
26. 雅安地震发生后，全国人民抗震救灾，众志成城，值地震发生一周年之际，某地政府又筹集了重建家园的必需物资120吨打算运往灾区，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示：（假设每辆车均满载）
车型
甲
乙
丙
汽车运载量（吨/辆）
5
8
10
汽车运费（元/辆）
400
500
600

(1)、全部物资可用甲型车6辆，乙型车5辆，丙型车辆来运送.

(2)、若全部物资都用甲、乙两种车型来运送，需运费8200元，问分别需甲、乙两种车型各几辆？

(3)、已知三种车的总辆数为14辆，你有哪几种安排方案刚好运完？哪种运费最省？

查看试题解析
27.

(1)、通过计算几何图形的面积可以表示一些代数恒等式，甲图是边长为 $x$ 的正方形，

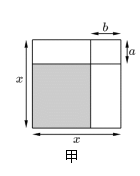
请用两种不同的方法表示甲图中阴影部分的面积（ $a$ ， $b$ 为常数）

①因式的积的形式：；

②关于 $x$ 的二次多项式的形式：；由①与②，可以得到一个等式：.

(2)、由（1）的结果进行应用：若 $(a - m) (a - 2) = a^{2} + n a + 6$ 对 $a$ 的任何值都成立，求 $m$ ， $n$ 的值

(3)、事实上，通过计算几何图形的体积也可以表示一些代数恒等式，乙图表示的是一个边长为 $x$ 的正方体挖去一个小长方体后重新拼成一个新长方体，请你根据乙图中图形的变化关系，利用整式乘法写出一个代数恒等式.

查看试题解析

车型	甲	乙	丙
汽车运载量（吨/辆）	5	8	10
汽车运费（元/辆）	400	500	600