2022-2023学年浙教版数学八年级下册4.3中心对称 课后测验
试卷更新日期:2023-03-15 类型:同步测试
一、单选题(每题4分,共40分)
-
1. 以下分别是回收、节水、绿色包装、低碳4个标志,其中是中心对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 下面图形中既是轴对称图形又是中心对称图形的是( )
3. 下面图形中既是轴对称图形又是中心对称图形的是( ) A、笛卡尔心形线 B、阿基米德螺旋线 C、科克曲线 D、赵爽弦图4. 下列银行标志中,既不是中心对称图形也不是轴对称图形的是( )A、
A、笛卡尔心形线 B、阿基米德螺旋线 C、科克曲线 D、赵爽弦图4. 下列银行标志中,既不是中心对称图形也不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 简简单单的七巧板能拼出千变万化的图形.殊不知七巧板作为中国传统玩具在国外也甚为流传,被称为“唐图”.下面四幅七巧板拼图的形状是中心对称图形的是( )A、
5. 简简单单的七巧板能拼出千变万化的图形.殊不知七巧板作为中国传统玩具在国外也甚为流传,被称为“唐图”.下面四幅七巧板拼图的形状是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 围棋起源于中国.古代称之为“弈”,至今已有4000多年历史.2017年5月,世界围棋冠军柯洁与人工智能机器人AlphaGo进行了围棋人机大战.截取对战机棋谱中的四个部分,由黑白棋子摆成的图案是中心对称图形的是( )A、
6. 围棋起源于中国.古代称之为“弈”,至今已有4000多年历史.2017年5月,世界围棋冠军柯洁与人工智能机器人AlphaGo进行了围棋人机大战.截取对战机棋谱中的四个部分,由黑白棋子摆成的图案是中心对称图形的是( )A、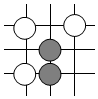 B、
B、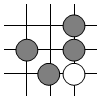 C、
C、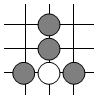 D、
D、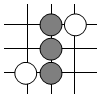 7. 下列如图交通标志中既是中心对称图形,又是轴对称图形的是( )A、
7. 下列如图交通标志中既是中心对称图形,又是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 8. 图①是苏州园林内的一种窗棂,图②是这种窗棂中的部分图案,该图案是由1个正六边形和6个全等的等边三角形组成的,则该图案( )
8. 图①是苏州园林内的一种窗棂,图②是这种窗棂中的部分图案,该图案是由1个正六边形和6个全等的等边三角形组成的,则该图案( ) A、既不是轴对称图形也不是中心对称图形 B、是中心对称图形但并不是轴对称图形 C、是轴对称图形但并不是中心对称图形 D、既是轴对称图形又是中心对称图形9. 下列说法中,错误的是( )A、角平分线上的点到角两边的距离相等 B、正方形的对角线互相垂直平分 C、斜边和一锐角对应相等的两个直角三角形全等 D、如果两个三角形全等,那么这两个三角形一定成中心对称10. 北京2022年冬奥会的开幕式上,各个国家和地区代表团入场所持的引导牌是中国结和雪花融合的造型,如图1是中国体育代表团的引导牌,观察发现,图2中的图案可以由图3中的图案经过对称、旋转等变换得到.下列关于图2和图3的说法中,不正确的是( )
A、既不是轴对称图形也不是中心对称图形 B、是中心对称图形但并不是轴对称图形 C、是轴对称图形但并不是中心对称图形 D、既是轴对称图形又是中心对称图形9. 下列说法中,错误的是( )A、角平分线上的点到角两边的距离相等 B、正方形的对角线互相垂直平分 C、斜边和一锐角对应相等的两个直角三角形全等 D、如果两个三角形全等,那么这两个三角形一定成中心对称10. 北京2022年冬奥会的开幕式上,各个国家和地区代表团入场所持的引导牌是中国结和雪花融合的造型,如图1是中国体育代表团的引导牌,观察发现,图2中的图案可以由图3中的图案经过对称、旋转等变换得到.下列关于图2和图3的说法中,不正确的是( ) A、图2中的图案是轴对称图形 B、图2中的图案是中心对称图形 C、图2中的图案绕某个固定点旋转60°,可以与自身重合 D、将图3中的图案绕某个固定点连续旋转若干次,每次旋转120°,可以设计出图2中的图案
A、图2中的图案是轴对称图形 B、图2中的图案是中心对称图形 C、图2中的图案绕某个固定点旋转60°,可以与自身重合 D、将图3中的图案绕某个固定点连续旋转若干次,每次旋转120°,可以设计出图2中的图案二、作图题(共2题,共20分)
-
11.(1)、已知六边形 ABCDEF是以O为对称中心的中心对称图形(如图),画出六边形 ABCDEF的全部图形;
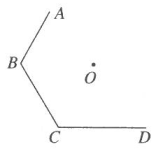 (2)、请你作出四边形ABCD关于点O的中心对称图形。
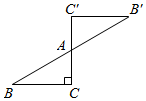
(2)、请你作出四边形ABCD关于点O的中心对称图形。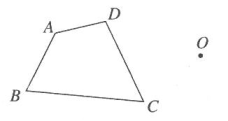 12. 如图,将置于平面直角坐标系中, , , .
12. 如图,将置于平面直角坐标系中, , , .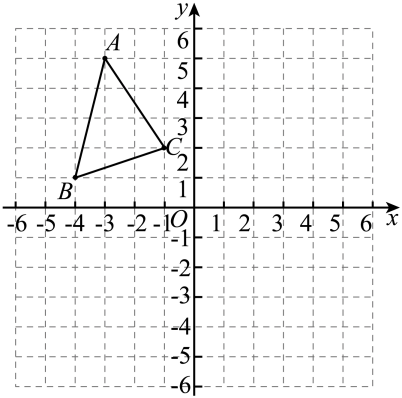
( 1 )将向右平移6个单位长度得到 , 请画出;
( 2 )以点O为对称中心,画出与成中心对称的;
( 3 )若将绕某一点旋转可以得到 , 请直接写出旋转中心的坐标.
三、解答题(共4题,共60分)
-
13.
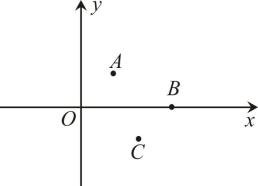
如图,已知点A(2,3)和直线y=x,
(1)点A关于直线y=x的对称点为点B,点A关于原点(0,0)的对称点为点C;写出点B、C的坐标;
(2)若点D是点B关于原点(0,0)的对称点,判断四形ABCD的形状,并说明理由.
 14. 在平面直角坐标系中,对于平面内任一点(m,n),规定以下三种变换:
14. 在平面直角坐标系中,对于平面内任一点(m,n),规定以下三种变换:①f(m,n)=(m,﹣n); ②g(m,n)=(﹣m,n); ③h(m,n)=(﹣m,﹣n).
(1)请你根据以上规定的变换,求f[g(﹣3,2)]的值;
(2)请你以点(a,b)为例,探索以上三种变换之间的关系.
15.如图,在平面直角坐标系中,△PQR是△ABC经过某种变换后得到的图形,观察点A与点P,点B与点Q,点C与点R的坐标之间的关系.在这种变换下:
(1)分别写出点A与点P,点B与点Q,点C与点R的坐标.
(2)从中你发现了什么特征?请你用文字语言表达出来.
(3)根据你发现的特征,解答下列问题:若△ABC内有一个点M(2a+5,1﹣3b)经过变换后,在△PRQ内的坐标称为N(﹣3﹣a,﹣b+3),求关于x的方程 -=1的解.
 16.
16.课外兴趣小组活动时,老师提出了如下问题:
 (1)、如图1,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
(1)、如图1,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
[感悟]解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(2)、解决问题:受到(1)的启发,请你证明下列命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.求证:BE+CF>EF,若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明.
四、填空题(每题5分,共30分)
-
17. 根据中心对称图形的性质可知,任何一对对应点的连线的就是该中心对称图形的对称中心,或两对对应点的连线的是对称中心
18. 写出一个轴对称图形但不是中心对称图形的四边形:19. 如图,的对角线、交于点 , 则图中成中心对称的三角形共有对.